基于位移观测序列聚类的边坡潜在滑移区早期辨识方法研究
时间:2023-11-02 来源:中国煤炭杂志官网 分享:煤矿安全
基于位移观测序列聚类的边坡潜在滑移区早期辨识方法研究
0 引言
边坡安全稳定问题长期困扰着露天煤矿的高效开采,是露天煤矿安全生产不可回避的关键问题[1-2]。近年来,随着GPS、边坡雷达、柔性测斜仪等新型自动化监测设备的广泛应用,露天煤矿边坡变形监测技术得到长足发展,为主动防控边坡灾害提供越来越多的现场数据支持[3-6]。相比而言,露天煤矿边坡风险判识技术明显滞后,大量观测数据没有得到充分挖掘与利用[7-9]。目前,边坡位移观测数据主要用于临滑险情预警,难以在潜在风险区的早期识别方面发挥作用。滑坡预测缺乏多源监测数据融合分析手段,通常仅围绕某个监测点的观测数据进行分析,边坡状态判识存在主观性和盲目性。
从系统辨识的角度看,边坡立体监测网不同空间点位处观测到的监测数据集蕴含边坡系统在外部应力作用下,由无序稳态向有序非稳态转换过程中时空全域演化的信息[10-12]。为挖掘隐藏在多源监测数据背后的边坡系统演化规律,一些学者引入数据挖掘领域中的聚类分析概念,对边坡观测数据进行特征提取和知识挖掘。秦雨樵等[13]综合考虑边坡各点的位移以及点安全系数,提出基于K-means聚类算法的滑面搜索方法;雷从雨[14]将边坡节点位移聚类分析与变点分析相融合,提出改进的特征点位移突变判据;陈波等[15]采用划分聚类和投影聚类对边坡位移监测资料进行测点区域划分和特征提取,以达到边坡监测数据简约的目的。
作为按观测时间先后顺序排列的一组数据序列,边坡位移观测序列表现出十分明显的非线性、非平稳特征,不仅序列内部相邻观测值存在关联性,而且序列之间存在不等长、偏移性、时间轴扭曲等结构差异。然而,现有研究工作普遍忽略了位移观测序列结构的复杂性,或者仅对观测序列中特定时刻的观测值进行聚类[13-14],或者虽然将整个观测序列看作聚类对象,但采用欧氏距离进行同步硬性度量[15],聚类结果的准确性和可靠性无法得到保证。为此,笔者提出一种将动态时间弯曲(DTW)距离和K-means(K均值)聚类相结合的无监督数据挖掘方法,从多源监测数据集中聚类“观测域上相近、空间域上连续、变形趋势明显”的监测点子集,将其所在区域圈定为潜在滑移区。实验结果表明,上述聚类方法能够在滑动面尚未完全形成阶段,提前辨识出边坡潜在滑移区域。
1 边坡动力灾害演化规律
露天煤矿边坡属于复杂非线性系统范畴,其动力演化遵循一般非线性系统演化所具有的普遍规律,即从无序到有序的演化历程[10-11]。在边坡灾害的早期阶段,各子系统基本保持力学平衡,整个系统处于最无序的平衡态;随着边坡高度、暴露面积、暴露时间的增加,在大气降水、开采扰动等外部应力的作用下,局部区域岩土体单元力学平衡状态被打破,应力重新分布,表现出短程相关和局部有序;在边坡灾害的中后期阶段,随着微损伤从小尺度到大尺度的串级发展以及主控滑动面的逐渐形成,各子系统趋向协同作用,表现为长程相关和全局有序,直至整个边坡系统发生突变而形成滑坡。
当边坡子系统发展到有序阶段时,所处区域上的监测点位移观测序列必然表现出相似的演化行为,即有序区域具有“观测域上相近、空间域上连续、变形趋势明显”的特点。因此,通过边坡立体监测网各测点的时空域数据进行聚类分析,可以对露天煤矿边坡系统的有序程度进行定量化表征,为边坡灾害的早期辨识与晚期预警预报提供支撑。
2 位移观测序列相似性度量方法
边坡位移观测序列是按观测时间先后顺序排列的数据序列,可以采用时间序列相似性度量方法进行相似性评价。时间序列相似性度量方法主要分为欧氏距离和DTW距离2种。欧式距离和DTW距离数据匹配如图1所示。
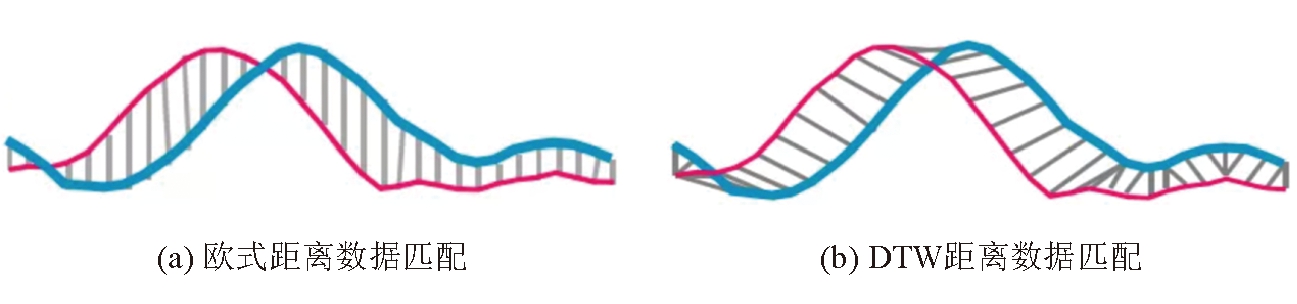
图1 欧式距离和DTW距离数据匹配
图1中蓝色曲线与红色曲线代表2个时间序列,灰色曲线代表2个时间序列元素之间的相似匹配关系,曲线两端代表2个元素。欧式距离是一对一元素相似匹配(蓝色曲线上的一个元素匹配红色曲线上的一个元素),DTW距离是一对多元素相似匹配(蓝色曲线上的一个元素有可能匹配红色曲线上的多个元素)。
2.1 欧氏距离
欧氏距离(ED)是一种对时间序列进行同步硬性度量(“一对一”匹配)的方法。设A=(a1,a2,…,an)和B=(b1,b2,…,bn)分别代表2个具有相同长度的位移观测序列,那么它们之间的欧氏距离定义为:
(1)
式中:d(A,B)——欧氏距离;
n——位移观测序列的长度,即观测时间的总次数;
ai——位移观测序列A中第i个观测值;
bi——位移观测序列B中第i个观测值。
d值越小说明序列A和B相似度越高,当d=0时,可认为A=B。
2.2 DTW距离
DTW距离是一种对时间序列进行异步相似形态度量(“一对多”匹配)的方法[16]。假定2个位移观测序列A=(a1,a2,…,an)和B=(b1,b2,…,bn),长度分别为n和m,则序列A和B的DTW距离计算过程如下。
2.2.1 距离矩阵
构造大小为n×m的距离矩阵:
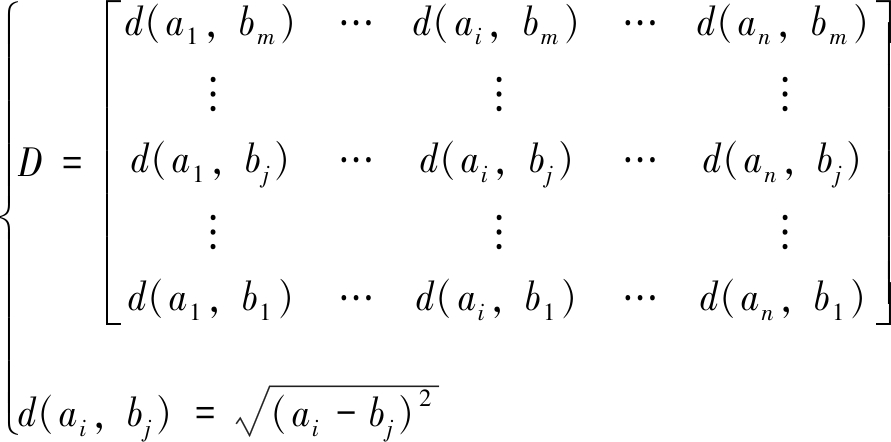
(2)
式中:d(ai,bj)——序列A中第i个观测值ai到序列B中第j个观测值bj的距离。
2.2.2 弯曲路径
定义弯曲路径:
(3)
式中:wr——序列A中第i个点与序列B中第j个点之间的匹配关系。
并且,弯曲路径需要满足3个约束条件:
(1)边界约束。弯曲路径起于距离矩阵D的左下角,止于距离矩阵D的右上角,即w1=(1,1),wk=(n,m)。
(2)单调性约束。对于相邻元素wr=(i,j)和wr+1=(i′,j′),需要满足i≤i′和j≤j′,即弯矩路径只能沿着时间轴单向移动。
(3)连续性约束。对于相邻元素wr=(i,j)和wr+1=(i′,j′),需要满足i′≤i+1和j′≤j+1,即弯曲路径上任意2个相邻的元素在距离矩阵D中也相邻。
2.2.3 DTW距离
定义序列A和B之间的DTW距离:
DTW(A,B)=min(∑(i,j)∈Wd(ai,bj))
(4)
由式(4)可知,DTW(A,B)对应的弯曲路径为最优路径,在此路径上的累积距离最小。基于动态规划,求解式(2)等价于构造累积距离矩阵Γ,其中的元素服从如下递归关系:
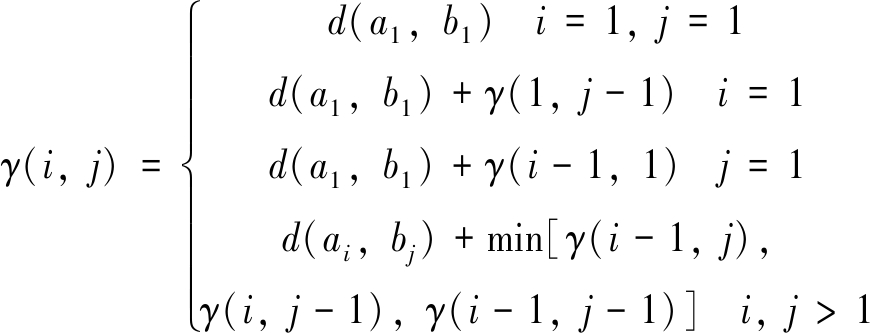
(5)
式中:γ(i,j)——累积距离。
当完成累积距离矩阵Γ计算后,元素γ(n,m)便为序列A和B的DTW距离,即:
DTW(A,B)=γ(n,m)
(6)
进一步,以Γ的右上角为起点,即wk=(n,m),以累积距离最小为选取原则,逆序寻找W中各元素,直至Γ的左下角,即w1=(1,1),可以得到完整的最优弯曲路径。
DTW距离不仅能实现不等长时间序列的度量,而且对时间序列的偏移、形状缩放、振幅变化、时间点异常数据具有较强的鲁棒性。因此,笔者采用DTW距离对位移观测序列的相似性进行分析。
3 位移观测序列相似性聚类方法
聚类分析一直是数据挖掘和机器学习研究的热点之一,其目的是将数据集中的数据点按各自的相似度划分为不同的簇类,并确保簇内的数据点相似程度最大、簇间数据点相似程度最小,从而判识数据集合的结构,提取需要的重要信息[17]。为深度挖掘位移观测序列背后蕴含的边坡系统演化规律,采用基于DTW距离的K-means聚类算法,对位移观测序列进行相似性聚类分析。
3.1 算法原理
假定数据集X由n个位移观测序列组成,Χ=(Χ1,Χ2,…,Χn),每个序列含m个观测值,Χi=(χi1,χi2,…,χim)。设定聚类数k,则聚类算法目标是找到一组簇类集合{S1,S2,…,Sk},使得簇间观测序列尽可能不同,而簇内观测序列尽可能相似。其中,每个簇的聚类中心由cj=(cj1,cj2,…,cjm)表示,1≤j≤k。具体K-means算法框架如下。
(1)初始化阶段。
步骤1:在数据集X中,随机选取k个观测序列作为初始聚类中心。
(2)聚簇阶段。
步骤2:遍历数据集X中所有的观测序列,根据各观测序列到每个聚类中心的DTW距离,将观测序列分配到距离最近的聚类中心所代表的簇中,构建k个子集{S1,S2,…,Sk}。
步骤3:计算每个子集的位移观测均值,作为新的聚类中心。
重复步骤2~3,直到k个聚类中心不再变化,或达到指定的迭代次数。在此过程中,每个观测序列有且仅属于一个簇,并且与该簇聚类中心之间的距离最小。
3.2 聚类中心计算
每个簇的聚类中心由该簇内观测序列各个时间点观测值的均值构成,相应计算公式如下:
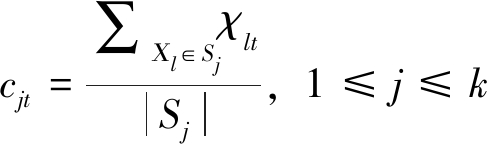
(7)
式中:cjt——簇Sj聚类中心cj第t个元素;
χlt——簇Sj内观测序列Χl第t个时间点的观测值;
|Sj|——簇Sj中观测序列的个数。
4 边坡潜在滑移区智能辨识
依据露天煤矿边坡系统所表现出的从无序到有序的动力演化特征,提出一种基于多源数据融合的边坡潜在滑移区辨识方法,通过对监测数据集的聚类分析,将“观测域上相近、空间域上连续、变形趋势明显”的监测点选定为有序测点,将有序测点所在区域圈定为潜在滑移区。具体辨识流程如下。
(1)以GPS、边坡雷达和柔性测斜仪等监测设备观测到的边坡位移监测数据为数据源,构建由N个监测点时空全域数据组成的监测数据集![]()
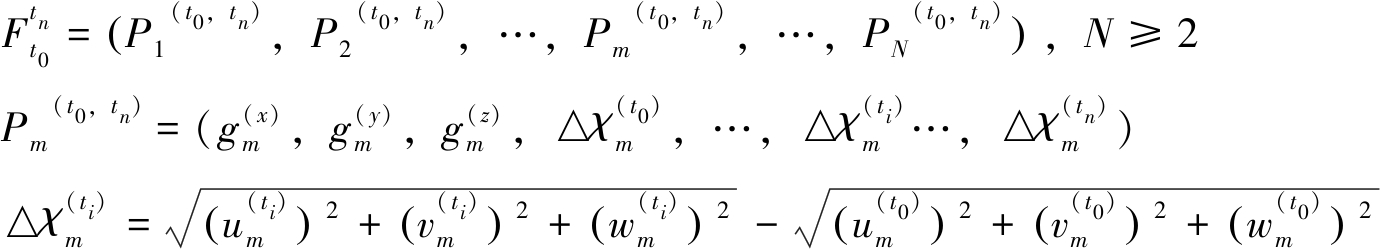
(8)
式中:![]() 第m测点的时空域数据,包括空间域上的位置坐标信息
第m测点的时空域数据,包括空间域上的位置坐标信息![]() 以及观测域上[t0,tn]时间段内观测位移信息
以及观测域上[t0,tn]时间段内观测位移信息![]()
![]() 时间段内第m测点观测到的合位移;
时间段内第m测点观测到的合位移;
![]() ——t0和ti时刻x、y、z 3个方向的位移分量。
——t0和ti时刻x、y、z 3个方向的位移分量。
(2)对监测数据集F进行数据清洗,消除数据集中的缺失值、重复值、异常值。
(3)设定聚类数k,采用基于DTW距离的K-means聚类算法,对F观测域上的位移序列进行相似性度量及聚类分析,将F分解为k个簇,每个簇中测点位移观测序列行为相近。计算同簇测点位移观测序列的均值,获得每个簇的聚类中心。
(4)对各簇中心进行排序,选出[t0,tn]区间位移变化最大的簇中心,并对该簇测点的空间连续性进行评估。如果存在连续性,则将该簇测点选定为有序测点,将该簇测点所在区域圈定为潜在滑移区。滑坡滑动面智能辨识的流程如图2所示。
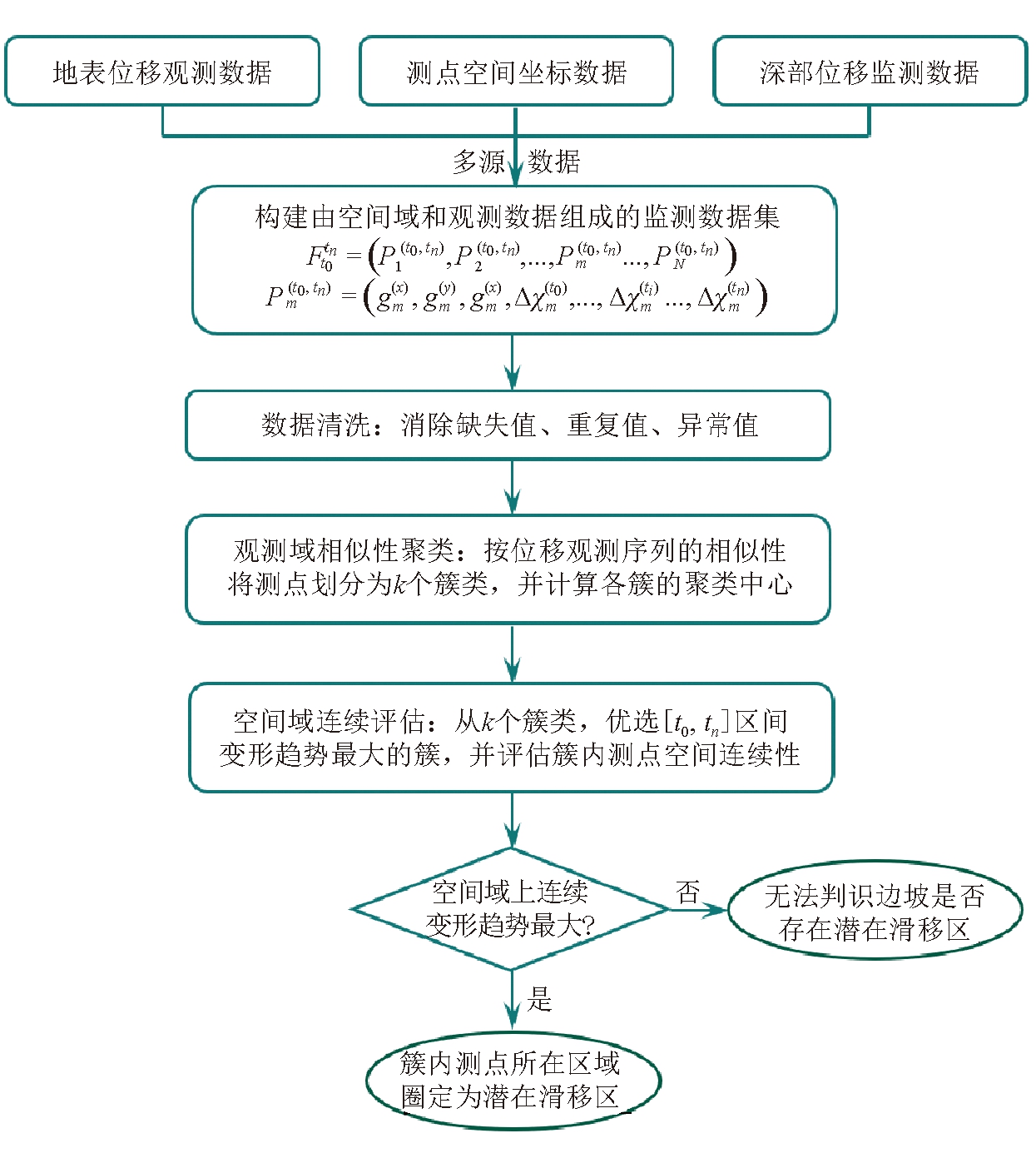
图2 边坡潜在滑移区智能辨识流程
5 实验研究与结果分析
采用有限元数值建模方式仿真模拟典型边坡渐进失稳全过程,输出边坡不同演化阶段的位移场作为实验测试样本,对提出的边坡潜在滑移区辨识方法展开适用性研究。
5.1 数值建模与计算
采用文献[18-19]中的边坡算例:边坡高度H=20 m,坡角β=26.57°,杨氏模量E=100 MPa,泊松比ν=0.3,容重ϒ=20 kN/m3,黏聚力c=10 kPa,内摩擦角φ=20°。土体材料为理想弹塑性材料,强度准则采用平面应变条件下莫尔-库仑结合DP准则(DP4准则)。边坡尺寸及网格划分如图3所示,边坡左、右两侧边界为法向约束,底边为双向固定约束,共划分四边形单元5 686个、节点5 878个。采用有限元强度折减方法,按照c/ω,tanφ/ω方式不断折减土体材料强度参数,模拟边坡渐进破坏过程及其位移场演化信息,直至边坡发生整体失稳。其中,ω为折减系数,可看作广义时间,其初始值ω0=1.0,步长△ω=0.002,第m步的折减系数ωm=ωm-1+△ω。
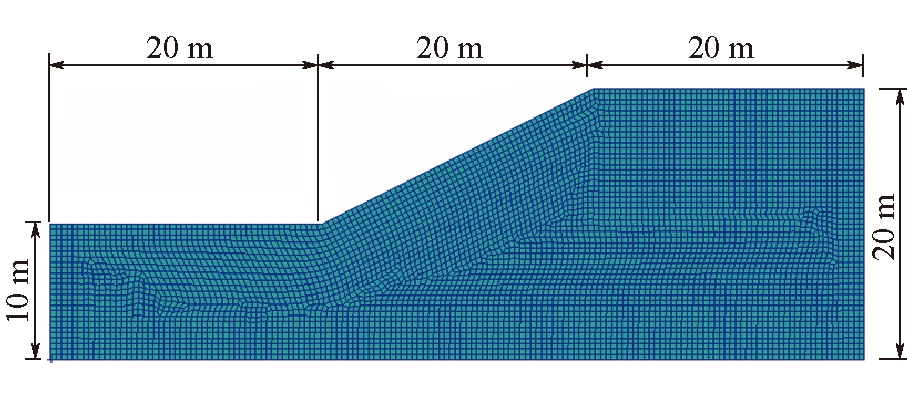
图3 边坡尺寸及网格划分
折减系数分别为ω90=1.18、ω150=1.30、ω185=1.36和ω192=1.384时,边坡等效塑性应变云图和局部化带扩展路径如图4所示。由图4可以看出,ω90、ω150、ω185和ω192时刻分别对应于边坡渐进演化的早期、中期、晚期和失稳阶段;当边坡处于前3个阶段时,虽然滑带自坡脚向坡体内部逐渐扩展,但整个滑带尚未贯通,滑移区也没有完全形成,无法通过塑性云图和滑带扩展路径提前辨识潜在滑移区;当边坡进入失稳阶段、滑带完全贯通后,通过塑性云图和滑带扩展路径可以准确获取滑移区范围。

图4 不同折减系数工况下边坡内部等效塑性应变云图及局部化带扩展路径
5.2 监测样本构建
将边坡模型中的所有节点选做监测点,以ωi0为观测起始时间,以ωn为观测截止时间,从数值模型计算结果中提取观测数据,构建边坡监测数据集。
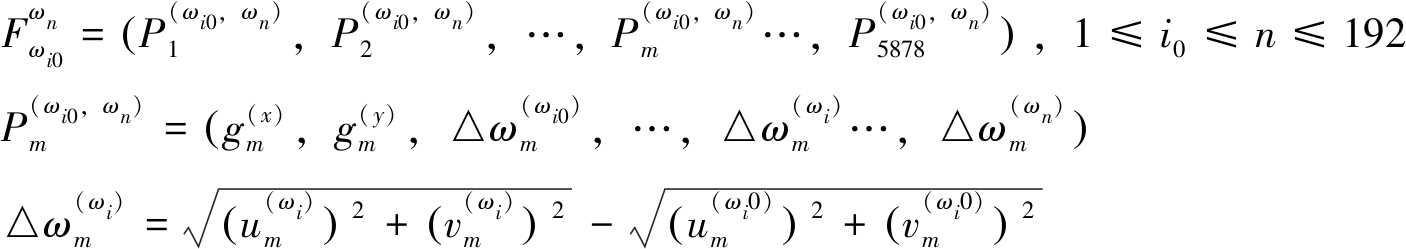
(9)
需要说明的是,受监测设备精度及周围场地环境影响,现场位移监测数据含有一定幅值的本底噪声。为此,监测数据集中的所有位移观测序列![]() 都随机添加噪声。随机噪声序列服从均匀分布,取值区间[0,2],单位mm。
都随机添加噪声。随机噪声序列服从均匀分布,取值区间[0,2],单位mm。
5.3 辨识算法测试
以观测起始时间为分类标准,将监测数据集细分为自边坡渐进演化的早期、中期、晚期启动观测的监测数据集,按照前文所述方法构建监测数据集。设定聚类数k=3,开展监测数据集观测域聚类。聚类结果通过测点空间分布图和簇中心曲线图可视化展示。其中,同簇测点及其簇中心曲线使用相同颜色。
5.3.1 边坡渐进演化早期阶段启动的观测数据集(简称“早期监测数据集”)
选取折减系数ω90=1.18(早期阶段)对应的时刻(ωi0=ω90)作为起始观测时间,选取ωn=ω140、ω155、ω175作为观测截止时间,构建3个具有不同观测时长的早期监测数据集![]() 早期监测数据集聚类结果如图5所示。由图5可以看出,对于
早期监测数据集聚类结果如图5所示。由图5可以看出,对于![]() 同簇测点在空间域上随机分布,各簇中心序列之间差异不大,不满足潜在滑移区辨识条件;
同簇测点在空间域上随机分布,各簇中心序列之间差异不大,不满足潜在滑移区辨识条件;![]() 和
和![]() 的聚类结果基本一致,同簇测点具有较强的空间连续性,不同簇中心具有显著的差异性,满足潜在滑移区辨识条件。由于簇C2具有最大簇中心位移,将该簇测点所在区域(棕色区域)圈定为潜在滑移区。与图4(d)比较可知,簇C2测点所在区域与边坡失稳后的实际滑移区非常吻合。
的聚类结果基本一致,同簇测点具有较强的空间连续性,不同簇中心具有显著的差异性,满足潜在滑移区辨识条件。由于簇C2具有最大簇中心位移,将该簇测点所在区域(棕色区域)圈定为潜在滑移区。与图4(d)比较可知,簇C2测点所在区域与边坡失稳后的实际滑移区非常吻合。
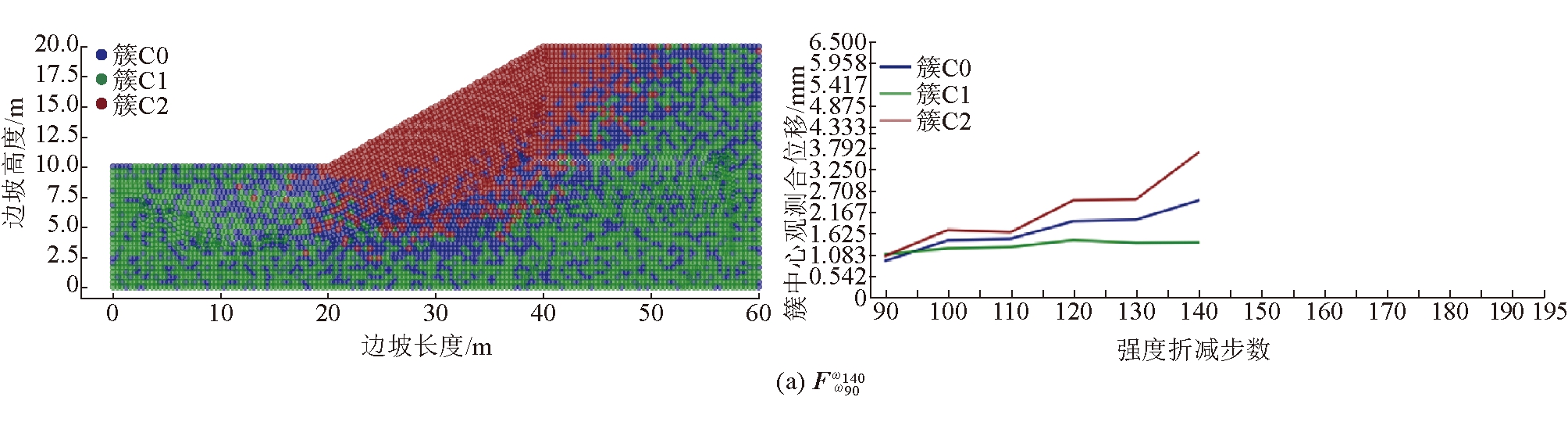
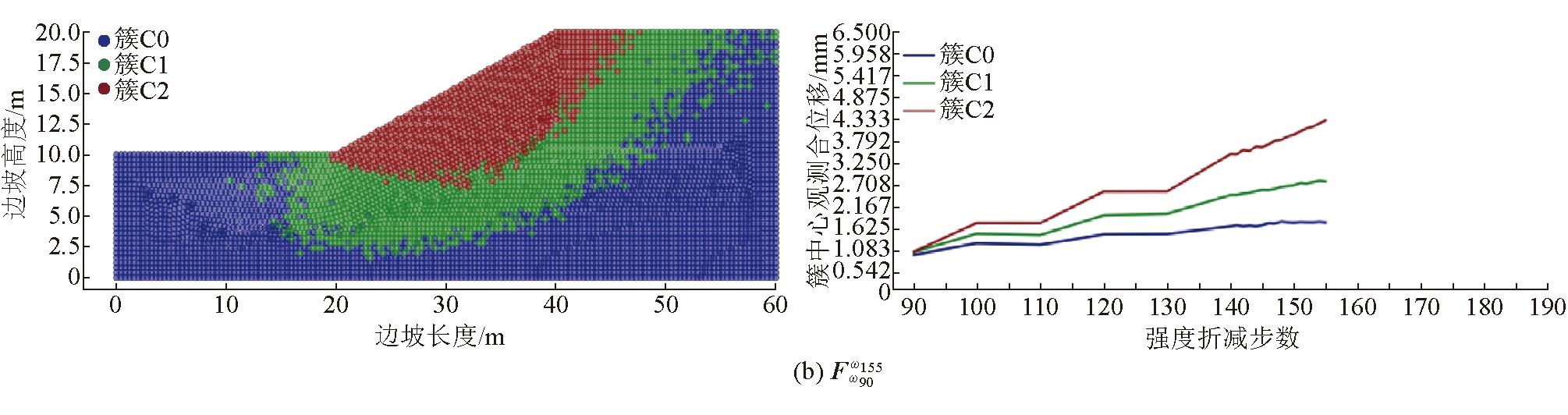

图5 同簇测点空间分布与簇中心曲线(早期监测数据集聚类结果)
5.3.2 边坡渐进演化中期阶段启动的观测数据集(简称“中期监测数据集”)
选取折减系数ω150=1.30(中期阶段)对应的时刻(ωi0=ω150)作为观测起始时间,选取ωn=ω155、ω175、ω185作为观测截止时间,构建3个具有不同观测时长的中期监测数据集![]() 中期监测数据集聚类结果如图6所示。由图6可以看出,
中期监测数据集聚类结果如图6所示。由图6可以看出,![]() 聚类结果空间不连续性,变形趋势不明显,不满足辨识条件;
聚类结果空间不连续性,变形趋势不明显,不满足辨识条件;![]() 和
和![]() 聚类后的簇C2具有最大簇中心位移,簇内测点空间连续分布,满足辨识条件。由簇C2测点圈定的潜在滑移区与图4(d)中的边坡失稳滑移区非常吻合。
聚类后的簇C2具有最大簇中心位移,簇内测点空间连续分布,满足辨识条件。由簇C2测点圈定的潜在滑移区与图4(d)中的边坡失稳滑移区非常吻合。
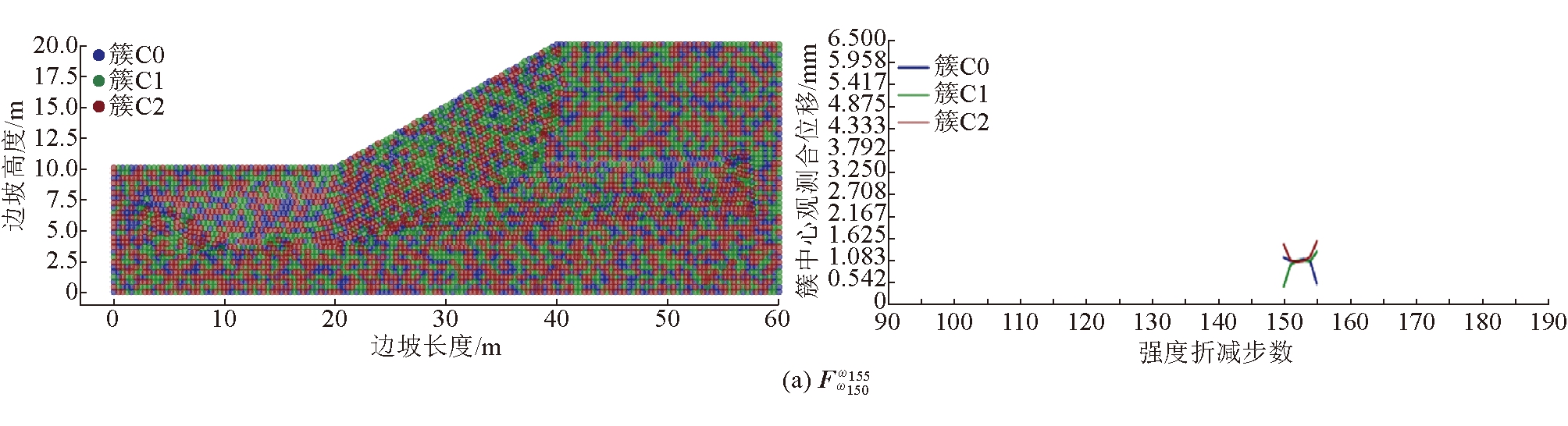
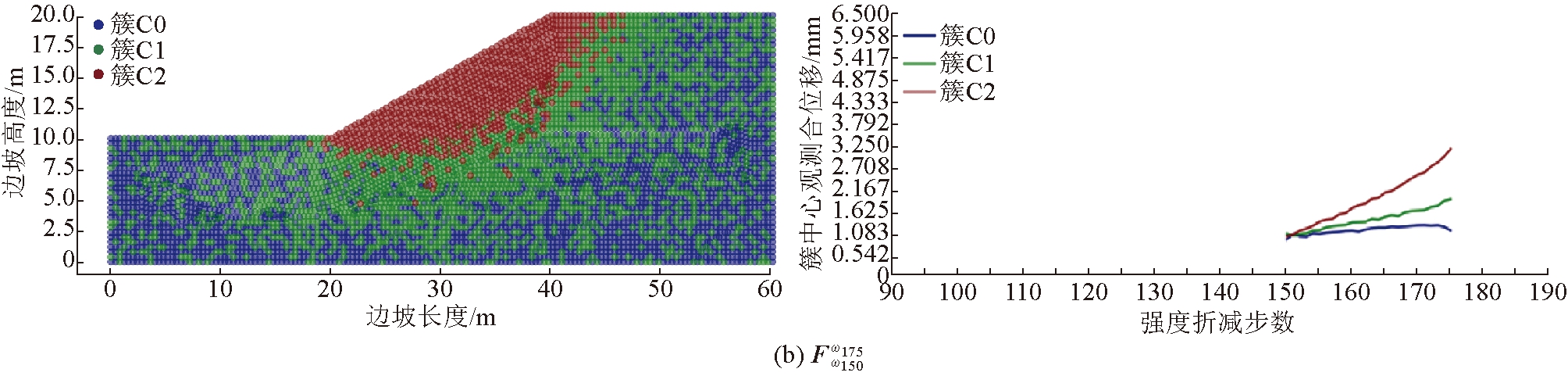
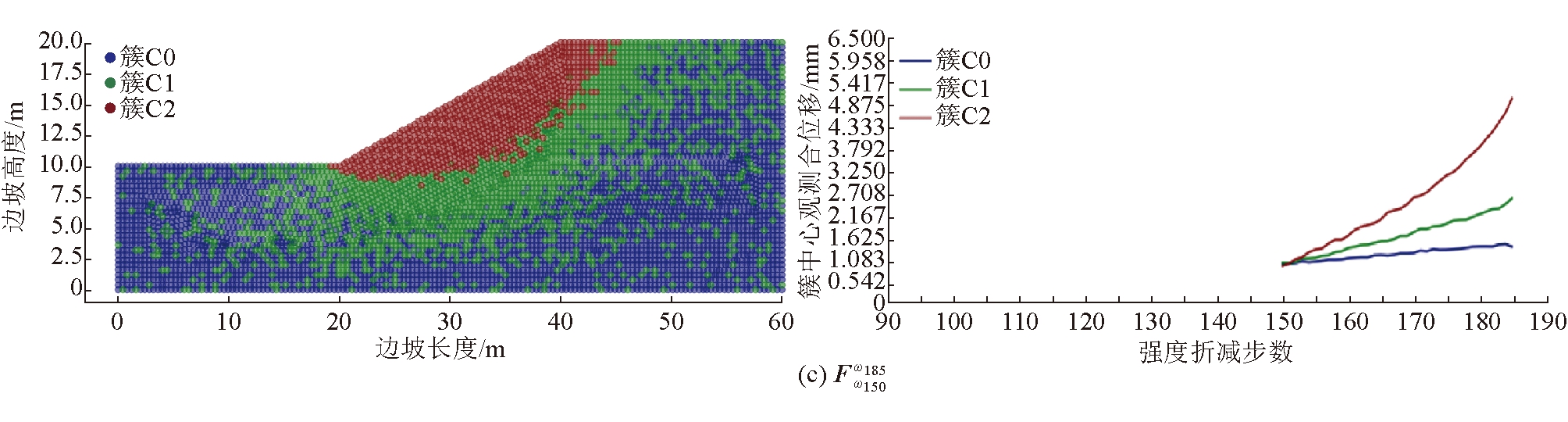
图6 同簇测点空间分布与簇中心曲线(中期监测数据集聚类结果)
5.3.3 边坡渐进演化晚期阶段启动的观测数据集(简称“晚期监测数据集”)
选取折减系数ω185=1.36(晚期阶段)对应的时刻(ωi0=ω185)作为起始观测时间,选取ωn=ω190作为观测截止时间,构建晚期监测数据集![]() 晚期监测数据集聚类结果如图7所示。由图7可以看出,聚类簇C2满足辨识条件。簇C2测点圈定的潜在滑移区与图4(d)中的边坡失稳滑移区十分吻合。
晚期监测数据集聚类结果如图7所示。由图7可以看出,聚类簇C2满足辨识条件。簇C2测点圈定的潜在滑移区与图4(d)中的边坡失稳滑移区十分吻合。
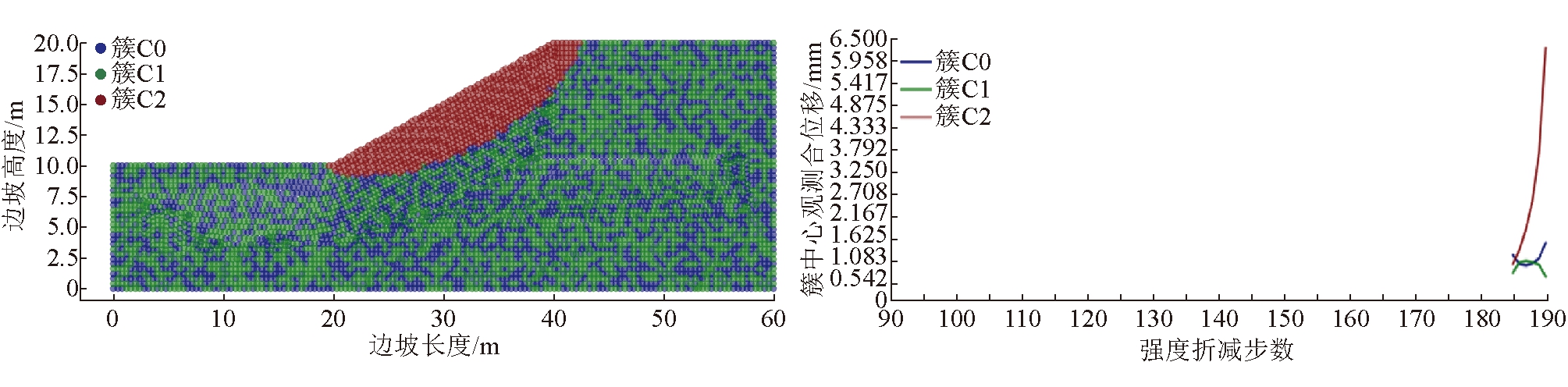
图7 同簇测点空间分布与簇中心曲线(晚期监测数据集聚类结果)
5.3.4 辨识结果分析
通过对早期、中期和晚期监测数据集的聚类挖掘,可以得到如下结论:
(1)通过对监测数据集的聚类分析,边坡无序到有序的渐进演化特征可以得到挖掘和体现,边坡潜在滑移区也能够得到早期辨识。![]() 的聚类结果都表明,“观测域上相近、空间域上连续、变形趋势明显”的测点簇所圈定的区域与边坡失稳后的实际滑移区域非常吻合。
的聚类结果都表明,“观测域上相近、空间域上连续、变形趋势明显”的测点簇所圈定的区域与边坡失稳后的实际滑移区域非常吻合。
(2)在监测点数量足够多的前提下,边坡潜在滑移区辨识效果将主要取决于观测的起始时间和观测的累积时长。观测起始时间越早,滑移区可辨识的时间也越早,但所需的观测时长也越多。以ω90为观测起始时间,于ω155时刻可辨识出潜在滑移区,需要65个时间步;以ω150为观测起始时间,于ω175时刻可辨识出潜在滑移区,需要25个时间步;以ω185为观测起始时间,滑移区辨识仅需要5个时间步,但辨识时间也最晚。
(3)现场位移监测数据中的本底噪声对辨识效果有很大影响,只有当观测累积位移值明显大于本底噪声时,才有可能对潜在滑移区进行聚类辨识。因此,选用观测精度高的监测设备对于潜在滑移区的早期辨识十分重要。
6 结论
(1)边坡立体监测网不同空间点位处观测到的监测数据集蕴含边坡系统在外部应力作用下,由无序稳态向有序非稳态转换过程中时空全域演化信息。为深度挖掘隐藏在多源监测数据背后的边坡系统演化规律,提出一种将DTW距离和K-means聚类相结合的无监督数据挖掘方法,从多源监测数据集中聚类“观测域上相近、空间域上连续、变形趋势明显”的监测点子集,将其所在区域圈定为潜在滑移区。
(2)采用强度折减有限元数值模型仿真模拟典型边坡渐进失稳全过程,输出边坡不同演化阶段的位移场作为实验测试样本,对潜在滑移区辨识方法展开适用性研究。实验结果表明,该聚类方法能够捕捉边坡系统从无序到有序的渐进演化特征,可以在滑动面尚未完全形成阶段,提前辨识出边坡潜在滑移区域。
(3)需要指出的是,采用数值模型构建监测样本与边坡现场观测数据之间存在差异,并且将所有节点都作为监测点是理想情况。因此,加快构建露天煤矿边坡地表-深部立体监测网,开展基于现场有限测点数据的潜在滑移区早期识别,将成为未来研究的重点。
[1] 孙玉科,杨志法,丁恩保.中国露天矿边坡稳定性研究[M].北京:中国科学技术出版社,1999.
[2] 赵锡刚.露天煤矿边坡地质灾害及其影响因素分析[J].现代矿业,2013(1):61-63.
[3] 丁震.露天煤矿边坡实时监测技术应用对比分析[J].煤炭技术,2017,45(9):186-192.
[4] 于玲,韩猛,鲁宁,等.基于GPS技术的露天煤矿边坡变形规律及趋势分析[J].煤矿安全,2019,50(8):232-235.
[5] 宋来臣,林毅斌.边坡雷达在露天矿山边坡滑坡预警的应用研究[J].煤炭技术,2021,40(7):119-121.
[6] 邱冬炜,祝思君,王来阳,等.利用阵列式位移传感系统进行地质灾害深部位移动态监测与分析[J].测绘通报,2018(3):122-125.
[7] 霍冬冬,亓星.多源数据融合在岩质滑坡监测预警中的应用[J].四川理工学院学报(自然科学版),2019,32(5):63-68.
[8] 王智伟,王利,黄观文,等.基于BP神经网络的滑坡监测多源异构数据融合算法研究[J].地质力学学报,2020,26(4):575-582.
[9] VILLALPANDO F,TUXPAN J,RAMOS-LEAL J A,et al.New framework based on fusion information from multiple landslide data sources and 3D visualization[J].Journal of Earth Science,2020,31(1):159-168.
[10] 许强,黄润秋.斜坡演化的自组织特征初探[J].中国地质灾害与防治学报,1997,8(1):7-11.
[11] 汪华斌,李江风,吴树仁.滑坡灾害系统非线性研究进展[J].地球科学进展,2000,15(3):271-276.
[12] 王乐一,赵文虓.系统辨识: 新的模式、挑战及机遇[J].自动化学报,2013,39(7):933-942.
[13] 秦雨樵,汤华,冯振洋,等.基于聚类分析的边坡稳定性研究[J].岩土力学,2018,39(8):2977-2983.
[14] 雷从雨.基于聚类-变点分析的强度折减法失稳判据改进研究[D].北京: 中国地质大学,2021.
[15] 陈波,詹明强,黄梓莘.基于时空聚类挖掘的库岸边坡位移监测数据约简[J].水利水运工程学报,2022,10(5):94-101.
[16] 李海林,梁叶,王少春.时间序列数据挖掘中的动态时间弯曲研究综述[J].控制与决策,2018,33(8):1345-1353.
[17] 王振武.数据挖掘算法原理与实现(2版)[M].北京: 清华大学出版社,2017.
[18] 刘晓宇,赵颖,刘洋,等.土质边坡极限平衡状态及临界滑动面的判定方法[J].岩石力学与工程学报,2012,31(7):1369-1378.
[19] GRIFFITHS D V,LANE P A.Slope stability analysis by finite elements[J].Geotechnique,1999,49(3):387-403.
Research on early recognition method for potential slip zone of slope based on displacement observation series clustering

移动扫码阅读
BAI Yu,SUN Junqing,LIU Mingming,et al. Research on early recognition method for potential slip zone of slope based on displacement observation series clustering [J].China Coal,2023,49(9):28-36.DOI:10.19880/j.cnki.ccm.2023.09.005
- 相关推荐
