基于遗传算法与BP神经网络的支架跟机自动化研究
时间:2023-03-08 来源:《煤炭科学技术》 分享:基于遗传算法与BP神经网络的支架跟机自动化研究
0 引 言
煤炭是我国一次能源中最经济可靠的资源,且可以通过科技进步实现煤炭资源的清洁高效利用[1]。2020年,我国的煤炭产量达38.4亿t,同比增长0.9%,是目前世界上最大的煤炭产量国和消费国。21世纪以来,我国煤炭开采技术及装备发展迅速,综采工作面生产先后经历了机械化和自动化2个阶段,目前正处于朝智能化开采转型时期[2],其中,我国煤炭开采的恶劣环境和装备条件是阻碍智能化发展最主要的2大因素[3-4]。研究综采工作面液压支架的跟机自动化、智能化技术,提高其自主跟机功能的实用性,全面实现综采工作面无人化,是减少煤矿安全事故的必要前提,也是我国煤炭行业亟待解决的重要难题[5]。
在液压支架支架跟机自动化过程中,采煤机的位置显得至关重要。以采煤机位置为基准,在其前侧的液压支架通过收护帮板,来防止采煤机的滚筒损伤护帮板,其后侧液压支架先完成降柱动作,再完成移架和升柱动作,确保对割煤后的悬空顶板及时支护。跟机自动化控制的目标是保证采煤机与液压支架、刮板输送机协同工作且互不干涉,在保证支护强度达到预期初撑力的前提下,确保其整体工作面的直线度。目前的液压支架跟机自动化研究中,高卫勇等[6]提出了一种涵盖中部、机头和机尾3个阶段的综采工作面液压支架跟机自动化工艺。雷照源等[7]提出大采高工作面跟机控制方法。冯帅[8]提出采煤机—液压支架相对位置融合校正系统。牛剑峰[9]提出支架自适应控制方案。刘清[10]提出放煤工作面支架姿态记忆控制方案。付翔等[11]提出支架群组跟机推进行为的智能决策模型。但目前的研究仅适应于单一环境,难以解决非线性动态问题。笔者将遗传算法和BP神经网络控制引入到综采工作面跟机自动化中,建立了GA-BP组合模型,研究其在动态环境下处理非线性的能力,以及对网络结构模型输出的预测值与实际值对比,得到误差拟合图。同时利用遗传算法来减小误差,提高精度和动态稳定性。
1 BP神经网络原理
BP神经网络,又称反向传播(Backpropagation, BP)网络模型,于1986年由Rumelhant和Hinton等人首次提出,是神经网络研究史上的重大里程碑[12],给非线性系统的研究提供了一个新的解决方法。BP神经网络在应用中,首先,对预测数据样本进行预处理,包括数据归一化及逆归一化处理等;其次,将数据输入至神经网络中,使其输出结果在训练过程不断达到收敛[13-14]。BP神经网络控制下的支架跟机移架原理如图1所示。
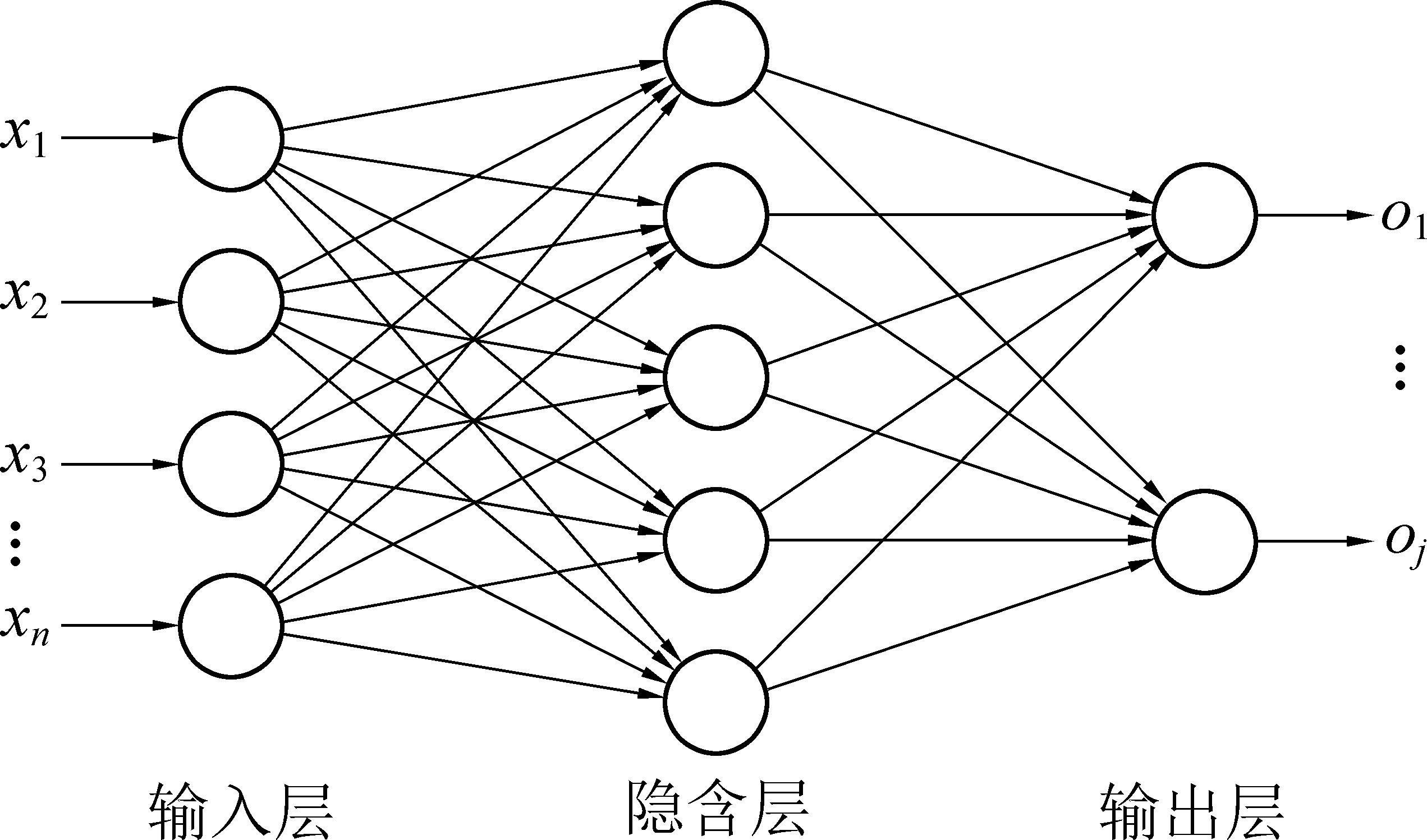
x1,x2,x3,…,xn—输入;o1,…,oj—输出
图1 BP神经网络结构
Fig.1 Structure of BP neural network
设Wij为输入层至隐含层的网络连接权值,Wjk为隐含层至输出层的连接权值。BP神经网络模型的本质是非线性函数,当存在n个输入、m个输出时,即表达了从n个输入至m个输出的非线性映射关系。
步骤1:将神经网络各层之间的参数和权值进行初始化,确定支架运动参数输入集X、移架距离输出集O、输入层层数n、隐含层层数l、输出层层数m、BP神经网络的学习速率和神经元的激励函数。
步骤2:计算BP 神经网络模型隐含层输出Hj,根据输入集X和连接权值Wij得到输出值。
(1)
式中:a为输入层与隐含层阈值,f为隐含层激励函数,激励函数的选择取决于模型的构建方式,常见的激励函数见表1,在数据样本规模不大的情况下,通常选择Sigmoid激活函数。
表1 各类激活函数及其表达式
Table 1 Various activation functions and their expressions

激活函数函数表达式Sigmoid函数f(x)=1/(1+e-ax)Relu函数f(x)=0,x<0x,x≥0 Tanh函数f(x)=ex-e-x /(ex+e-x)softmax函数f(x)=eix∑kk=1ekx斜面函数f(x)=T,x>ckx,x≤c-T,x<-c
步骤3:输出层计算。根据步骤2得到的隐含层输出Hj,将它输入到隐含层与输出层网络中,来计算神经网络模型的移架距离,其中,输出层与隐含层的阈值为b,其计算过程为
(2)
步骤4:重新调整连接层之间的权值,用BP神经网络模型预测的移架距离Ok与实际需求值Y作比较,取Ok与Y的差值绝对值,得到网络模型的预测误差e。以e为标准,使得输出结果达到收敛为止,最终完成对权值的迭代替换,更新权值的计算为
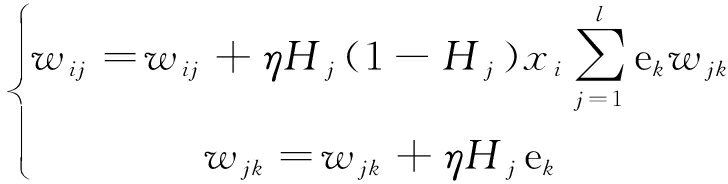
(3)
式中:η为学习率,ek=Yk-Ok。
步骤5:更新隐含层和输出层的阈值,利用式3计算的预测误差ek,更新替换模型的阈值a和b。
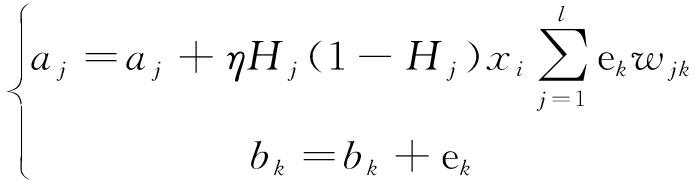
(4)
根据以上步骤来更新各参数值,若输出的移架距离已经达到预期误差精度,则可以直接输出结果;否则,跳到步骤2重新计算,直至达到精度要求。
2 遗传算法原理
遗传算法可以模拟生物社会中的个体进化,自适应搜索优化问题的最优解,同时还能够进行有效的局部搜索,找出潜在的优化解[15]。在输入算法的进程中,可根据得到的信息来逐步寻找最佳信息。
在利用遗传算法求解输入集X和O之间的阈值和权值过程中,引用二进制编码来代表输入集与输出集的变量。二进制编码等效于个体的基因段,而整个算法的个体正是由这些基因段构成[16-17]。基因段个体又属于遗传算法种群的组成部分,并遵循自然界中适者生存的法则。在延续后代时,采用轮盘赌方式选择合适个体,达到一定遗传代数操作后,会得到一个能适应环境的最优种群,即问题的最优解决方案。基本的遗传运算、二进制编码、参数选择和适应度函数构成了遗传算法的整体架构[18-19]。
其中,遗传算法的自适应能力主要体现在输出的移架距离能否满足现场实际需求,进而调整自身的反馈能力。在进化过程中,如果输出移架距离可以较好地满足工作面生产要求,并保证其直线度,那就找到了一个较好的进化模式,并且在算法设计中应该尽可能地保留该模式[20]。否则,此种模式很可能会被模型淘汰。GA算法的适应性主要取决于交叉概率Pc和变异概率Pm。
3 跟机移架模型的构建
BP神经网络虽然可以解决非线性问题,但是输出准确率与训练速度仍难以满足实际需求。因此,在其基础上补充遗传算法来优化模型,从而弥补BP神经网络控制的缺陷。
3.1 数据的预处理
由传感器获取相关的训练数据集,变量的动态浮动范围必须与实际现场数据保持一致。一般情况下,液压支架的移架行程范围在0~100 cm之间。因此,应该选择合理的数据集,删除异常的数据,异常数据集范围定义为(100,200)cm。
3.2 GA-BP组合模型的构建
步骤1:遗传算法参数初始化。将跟机过程中的移架时间和工作面倾角作为模型的输入部分,移架距离作为输出部分。对组合模型进行初始化处理,在Matlab环境下进行训练,具体的工控机配置与组合模型参数如下:

处理器Inter i7, 2.5GHz输入层节点2输出层节点1最大迭代次数100精度1.00e-6隐含层层数5操作系统win10,64位软件MATLAB学习率0.01训练方法learngdm输出维数1动量因子0.7
第1代种群数目设为10,以保证群体中个体具有足够的种群多样性。最大进化代数设为20。交叉概率和变异概率选取经验值,分别为Pc=0.2,Pm=0.1。GA算法优化进化停止准则设为:达到最大进化代数20或适应度值连续几代保持在1.0e-6。
步骤2:随机选择2个输入集数据进行交叉,产生一行两列的矩阵,检测矩阵是否有0,若有则重新生成随机数。最终得到的随机数小于交叉概率,则可以进行交叉。第k个染色体ak与第i个染色体ai在第j次交叉,其公式为
akj=akj(1-b)+aijb
(5)
aij=aij(1-b)+akjb
(6)
式中,b为生成的随机数。
步骤3:随机选择一个输入数据,如果生成的随机数大于变异概率,则可以进行变异。假设选择了第i个染色体的第j个基因,其公式为
(7)
(8)
式中:amax为基因aij的上界,amin为基因aij的下界,g为当前迭代次数,Gmax为最大进化次数,τ为(0,1)之间的随机数。
步骤4:使用适应度函数计算移架距离的适应度值,并绘制适应度曲线。
步骤5:训练数据的个体进化结束后,由于进化方向是随机不确定的,chrom函数会控制测试数据中的个体朝着训练数据中最优个体的方向进化,从而可以大幅提高测试数据的适应度值。将每一代进化的适应度种群进行比较,通过淘汰适应度差的个体,保留适应环境进化程度高的个体。
4 跟机移架仿真与分析
4.1 GA-BP组合模型仿真
通过上述参数设置进行初始化,取神东煤炭集团榆家梁煤矿43101工作面2 000组数据作为样本,随机取1 900组数据构成训练数据集,剩余的100组数据构成测试数据集。GA-BP组合模型利用train函数对训练数据集进行训练,再利用测试数据集验证输出。以推移距离(0,40)cm为例,液压支架预测的推移行程如图2所示。
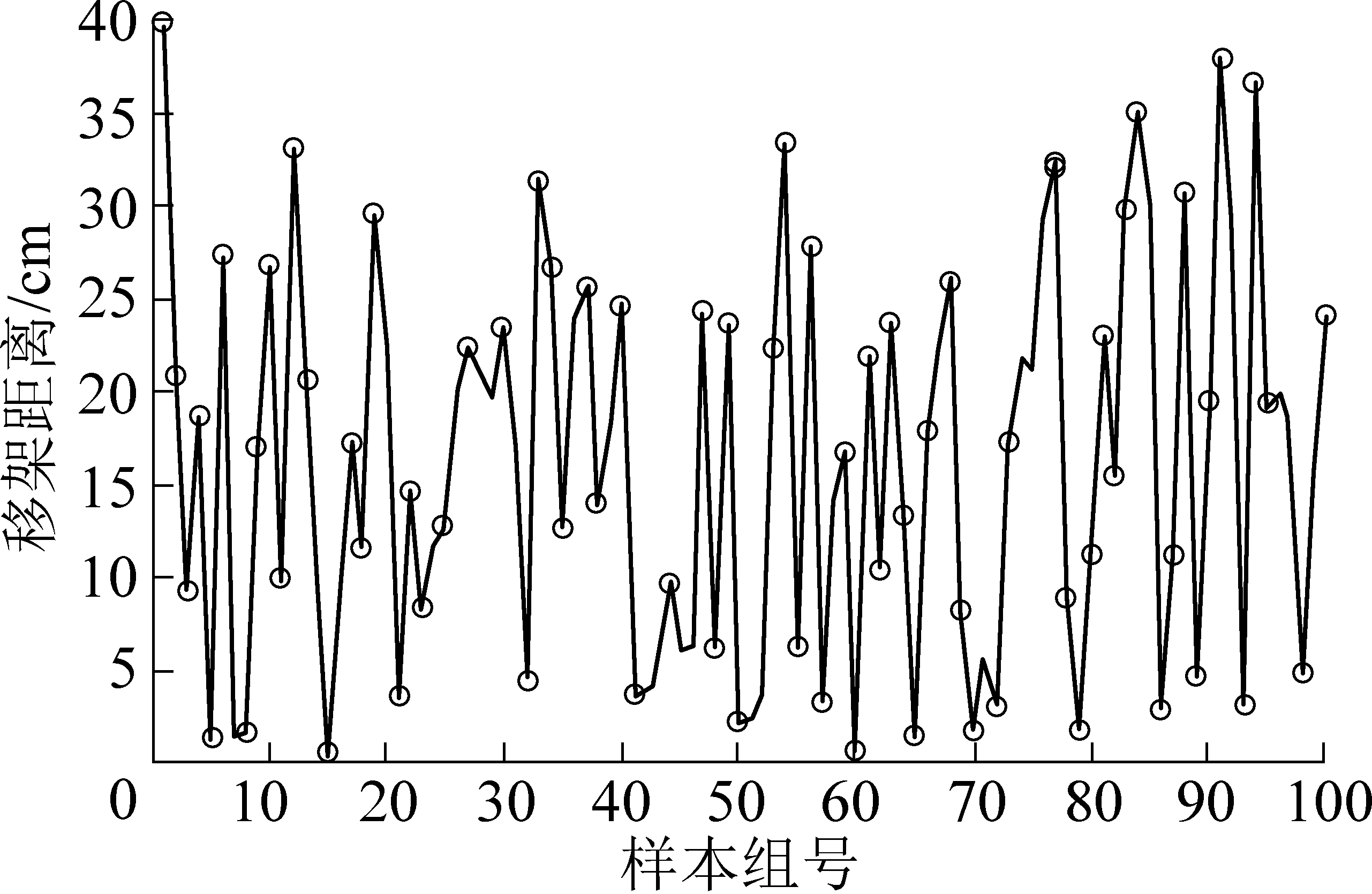
图2 GA-BP组合模型移架距离预测
Fig.2 Prediction of moving distance based on GA-BP combination model
将得到的移架距离数据代入式9,可得GA-BP组合模型预测误差比如图3所示。
(9)
式中:p为期望输出,q为预测输出,w为误差百分比。由图3可得,样本的最大误差不超过0.045%,整体平均准确率达99.5%。
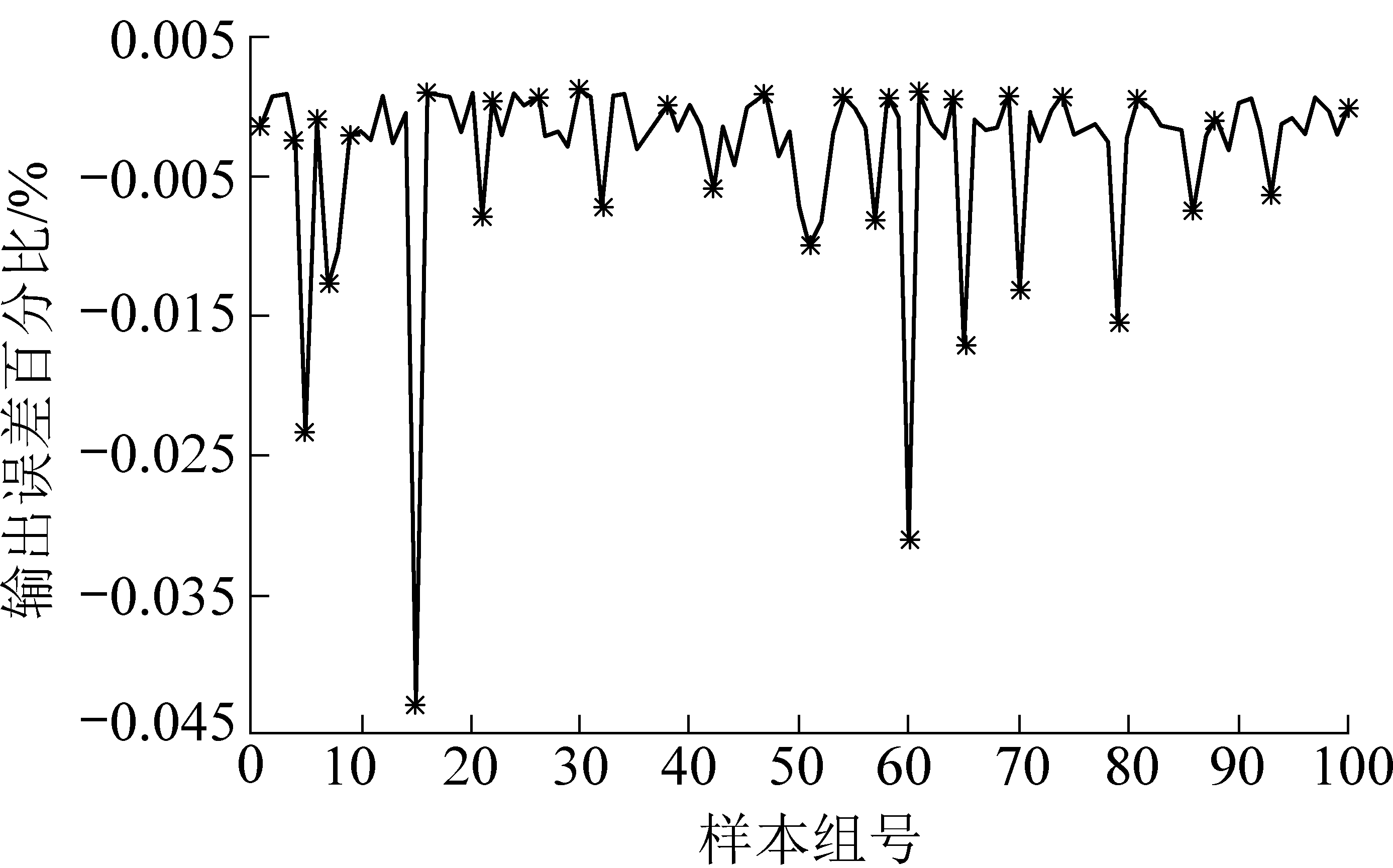
图3 GA-BP组合模型预测误差百分比
Fig.3 Prediction error percentage of GA-BP combination model
4.2 遗传算法的优化
图4为GA- BP组合模型的拟合精度,其中回归系数 R 接近于 1,证明在模拟液压支架推移行程时,可以近似视为线性拟合函数。

图4 回归系数
Fig.4 Regression coefficients
由图5—图7可知,BP神经网络模型虽然在第26次迭代时才达到收敛,但最小均方误差值达到1.0956e-5,不符合精度要求。
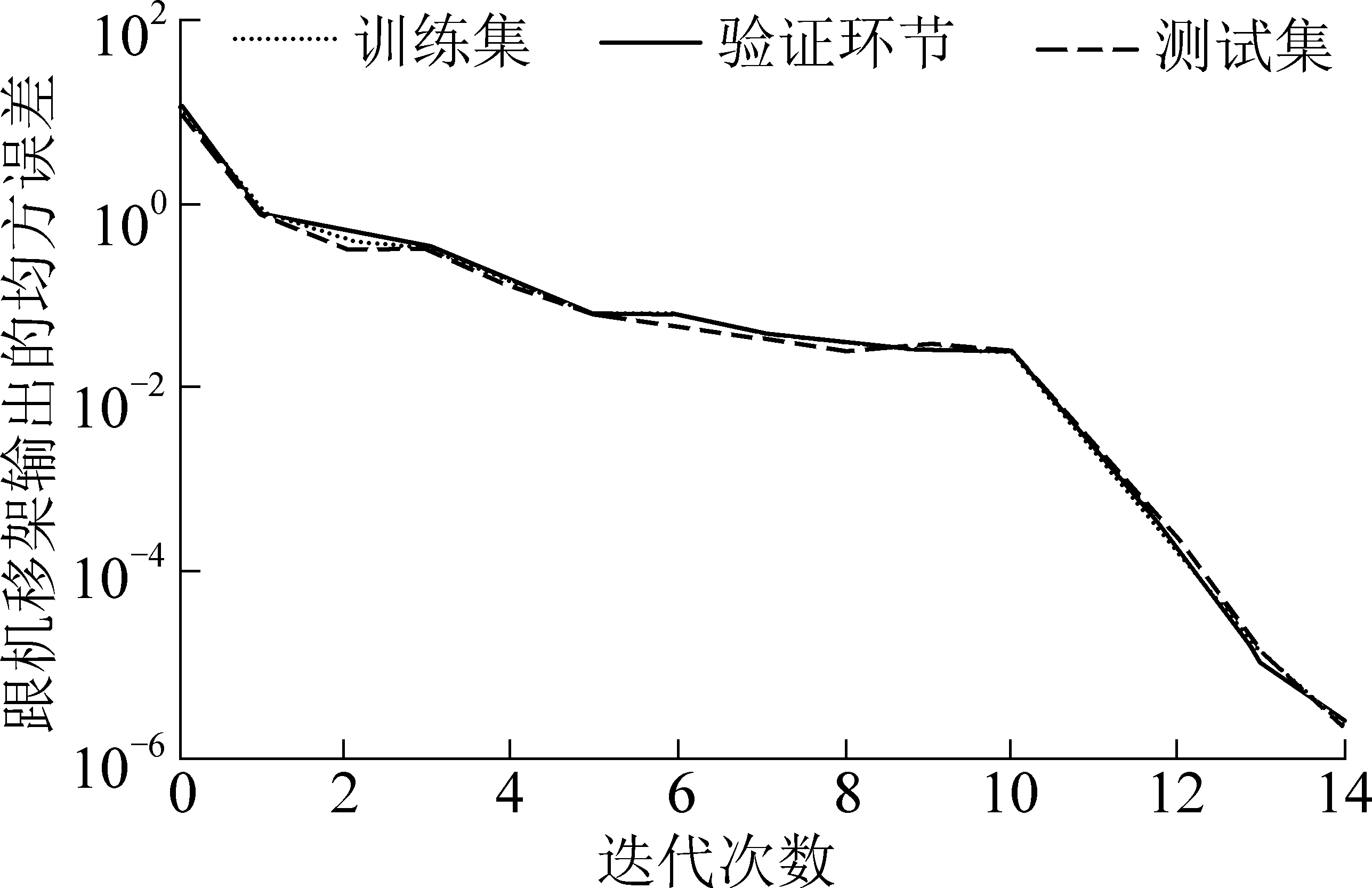
图5 GA-BP组合模型均方误差
Fig.5 Mean square error of GA-BP combination model
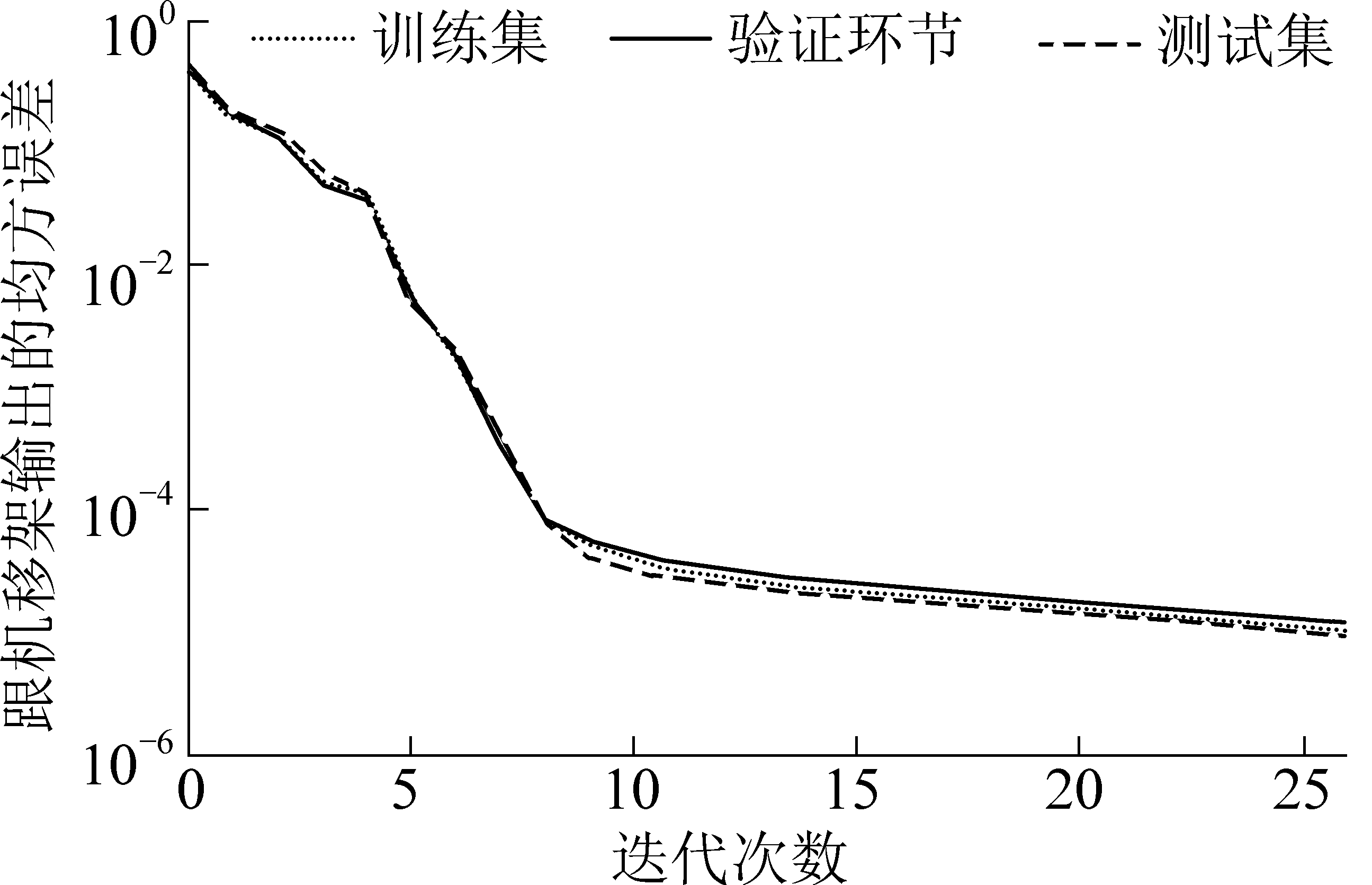
图6 BP神经网络模型均方误差
Fig.6 Mean square error of BP neural network model
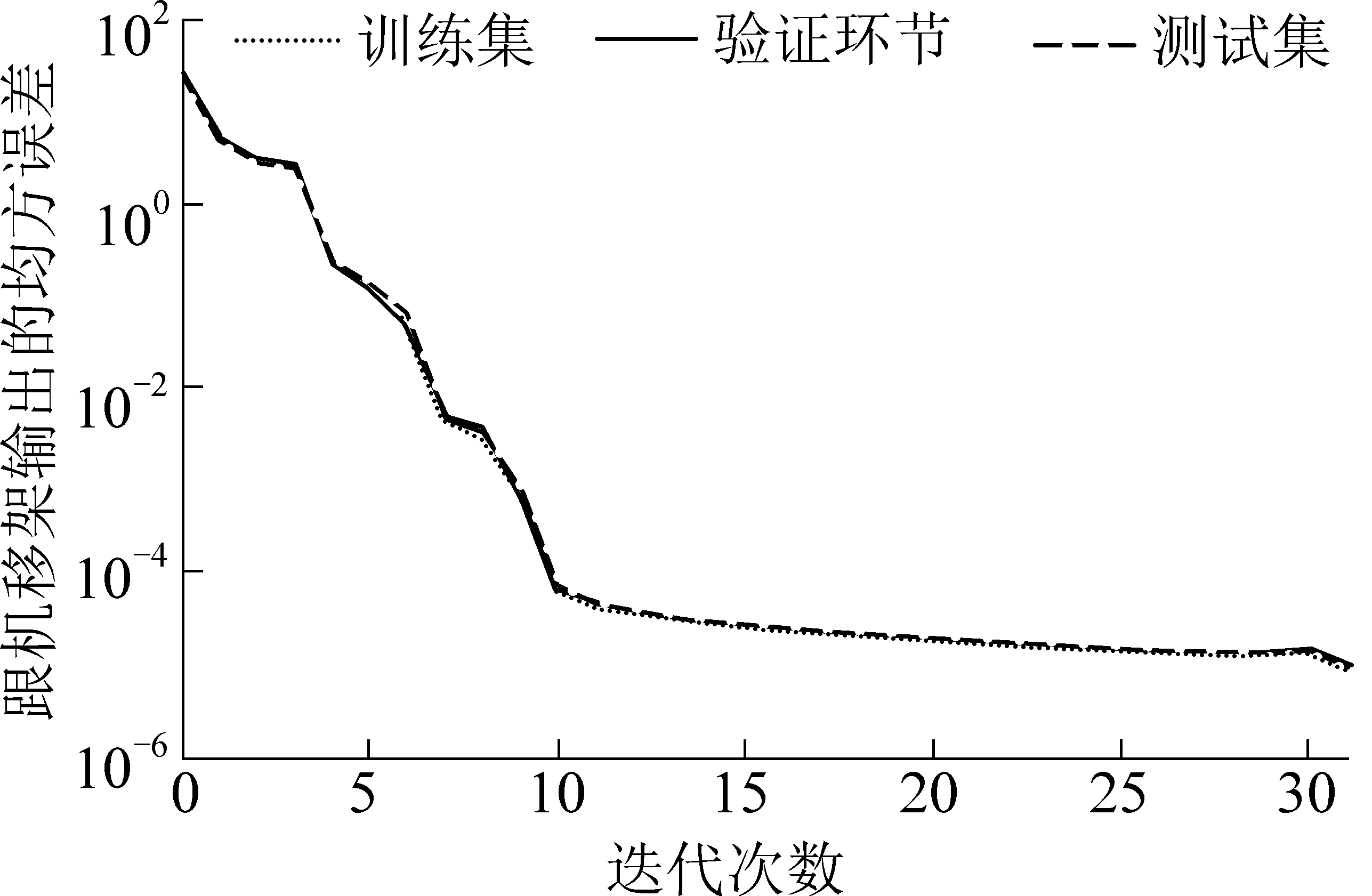
图7GA模型均方误差
Fig.7 Mean square error of GA model
而GA模型最小均方误差值达到了9.4098e-6,但是共迭代31次,次数过于繁多;通过3者对比,GA-BP组合模型在训练速度(14次)以及预测准确性(均方误差为2.4282e-6)2个方面都要优于BP神经网络模型和GA模型。
适应度曲线如图8所示,可知在第15代以后,种群适应度基本处于收敛状态,第20代已终止。遗传算法在进化搜索中基本不利用外部信息,也不对函数求梯度,仅根据适应度函数,通过种群个体的适应度来进行检索。
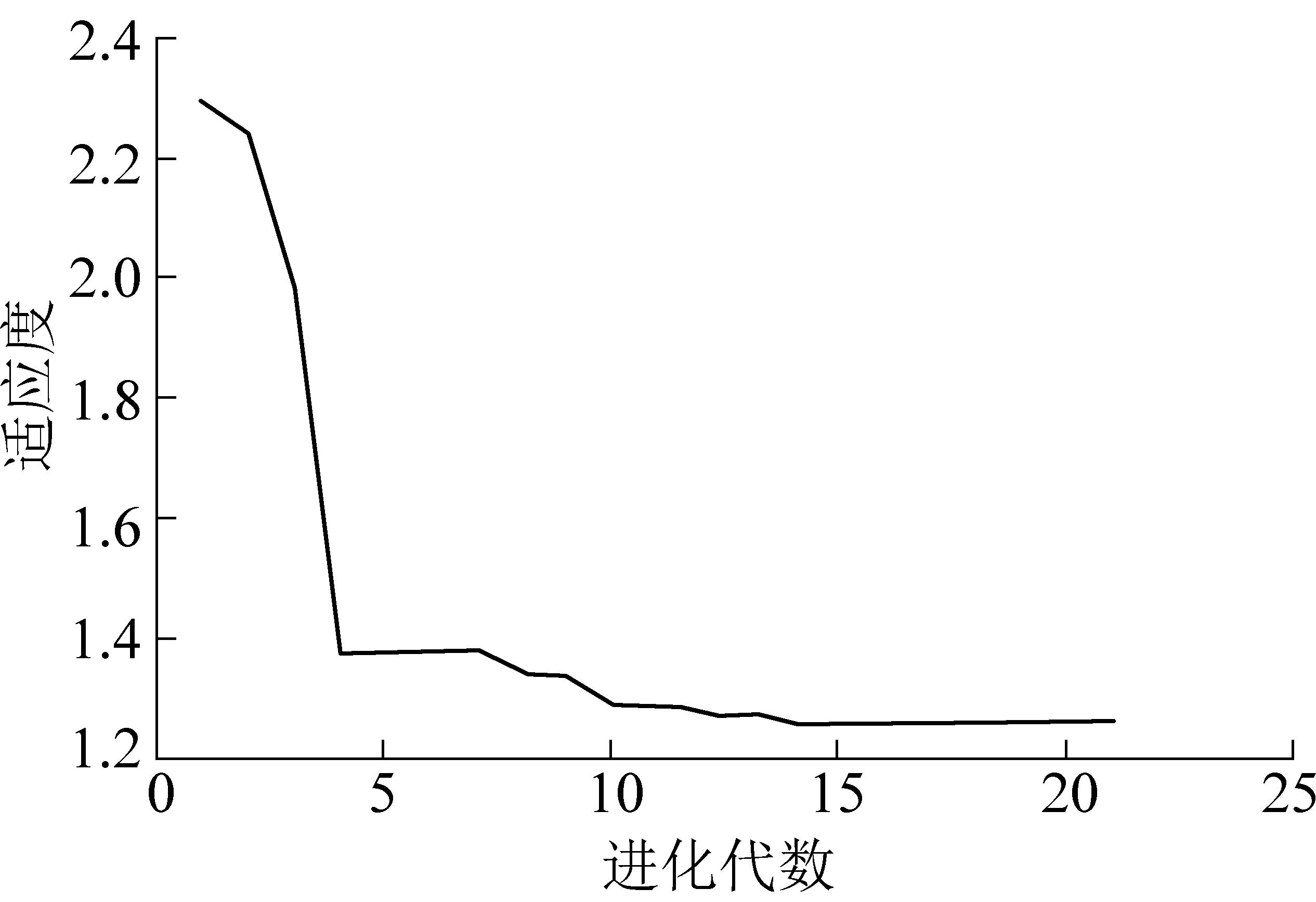
图8 适应度曲线
Fig.8 Fitness curve
5 结 论
提出了一种基于遗传算法与BP神经网络的液压支架跟机自动化方法,取得的结论主要有:
1)建立了GA-BP组合模型,将移架时间和工作面倾角作为输入层,设置5个隐含层,将移架行程作为输出层,为液压支架跟机移架找直提供了理论支持。
2)研究对比了BP神经网络模型、GA模型和GA-BP组合模型,得到的仿真数据图,结果表明:①GA-BP组合模型准确率比BP神经网络高出5倍多,而且比GA模型响应速度更快,仅在第14次迭代达到收敛;②在添加遗传算法后,GA-BP组合模型的回归基本趋近于线性,表明在液压支架跟机模型中,可以视为线性拟合系统;③在适应度曲线中,种群在迭代第5次后就趋于收敛且在第20代时保持不变,表明模型具有较高的快速性和稳定性
参考文献(References):
[1] 王国法,刘 峰,孟祥军,等.煤矿智能化(初级阶段)研究与实践[J].煤炭科学技术,2019,47(8):1-36.
WANG Guofa, LIU Feng, MENG Xiangjunet al.Research and practice of coal mine intellectual (primary stage)[J]. Coin Science and Technology, 2019,47(8):1-36.
[2] 李首滨.煤炭智能化无人开采的现状与展望[J].中国煤炭,2019,45(4):5-12.
LI Shoubin.Current status and prospects of intelligent mining of coal[J].China Coal, 2019,45(4):5-12.
[3] 张利军. 综采工作面供电供液系统优化及自动化技术研究与应用[D].徐州:中国矿业大学,2019.
ZHANG Lijun, Research and application of power supply and liquid supply system optimization and automation technology in fully mechanized mining working[D].Xuzhou:China University of Mining and Technology,2019.
[4] 张步勤. 薄煤层综采自动化关键技术及应用研究[D].北京:中国矿业大学(北京),2015.
ZHANG Buqin. Research of key technology in application of coal seam fully mechanized mining automation[D].Beijing:China University of Mining and Technology(Beijing),2015.
[5] 张 霖.液压支架自主跟机关键技术研究[D].徐州:中国矿业大学,2017.
ZHANG Lin.Research on Key Technology of Autonomous Follow-up of Hydraulic Support[D].Xuzhou:China University of Mining and Technology,2017.
[6] 高卫勇,张敏娟.综采工作面液压支架跟机自动化工艺研究[J].工矿自动化,2018,44(11):14-17.
GAO Weiyong,ZHANG Minjuan.Research on automation technology of hydraulic support and machine in fully mechanized coal mining[J].Industrial and mining automation,2018,44(11):14-17.
[7] 雷照源,姚一龙,李 磊,等.大采高智能化工作面液压支架自动跟机控制技术研究[J].煤炭科学技术,2019,47(7):194-199.
LEI Zhaoyuan,YAO Yilong,LI Lie,et al.Research on the control technology of automatic follow-up of hydraulic support for large mining height intelligent working [J].Coin Science and Technology,2019,47(7):194-199.
[8] 冯 帅.采煤机—液压支架相对位置融合校正系统关键技术研究[D].徐州:中国矿业大学,2015.
FENG Shuai.Research on key technology of shearer-hydraulic support relative position fusion correction system[D].Xuzhou: China University of Mining and Technology, 2015.
[9] 牛剑峰.液压支架自适应控制系统设计[J].煤矿机电,2019,40(5):8-11.
NIU Jianfeng.Design of adaptive control system of hydraulic support[J].Coal Mine Electrical,2019,40(5):8-11.
[10] 刘 清,孟 峰,牛剑锋.放煤工作面支架姿态记忆控制方法研究[J].煤矿机械,2015,36(5): 89-92.
LIU Qing,MENG Feng, NIU Jianfeng.Research on the control method of posture memory of coal support[J].Coal mining machinery, 2015,36(5): 89-92.
[11] 付 翔,王然风,赵阳升.液压支架群组跟机推进行为的智能决策模型设计[J/OL].煤炭学报: [2020-05-26]1-13.
FU Xiang,WANG Ranfeng, ZHAO Yangsheng.Design of intelligent decision model for the follow-up propulsion behavior of hydraulic support group[J/OL]. Journal of China Coal Society,[2020-05-26]1-13.
[12] 邢家龙.基于改进狼群算法和BP循环神经网络的短时交通流预测研究[D].北京:北京交通大学,2019.
XING Jialong.Research on short-term traffic flow forecast based on improved wolf pack algorithm and BP recurrent neural network[D].Beijing:Beijing Jiaotong University,2019.
[13] JUAREZFR. Measurement and analysis of the roof pressure on hydraulic props inlongwall[J]. Internationa Journal of Coal Geology,2008, 75(1): 49-62.
[14] FRANCISCO P,MARCEL C.Forecasting based on an ensemble autoregressive moving average-adaptive neuro-fuzzy inference system-neural network-genetic algorithm framework[J]. Energy,2020,197.
[15] 张 涛.基于复杂网络理论的遗传算法分析与设计[D].南京:南京邮电大学,2019.
ZHANG Tao.Analysis anddesign of genetic algorithm based on complex network theory[D].Nanjing:Nanjing University of Posts and Telecommunications, 2019.
[16] MO X,GE W,WNAG S, et al. Mechanical design and dynamics simulation of locust-inspired straight line four-bar jumping mechanism[M].Singapore: Springer, 2017: 429-442.
[17] SCHMIDT L,ANDERSEN T O,PEDERSEN H C.On application of second order sliding mode control to electro-hydraulic systems[C],ASME,Biennial Conference on Engineering Systems Design and Analysis, 2014: V003T15A018-V003T15A018.
[18] SAYED, HABIBI. Inner-loop control for electro-hydraulic (eha) actuation systems[J]. Journal of Dynamic Systems, Measurement, and Control, 2011, 134(1):1-8.
[19] HAS,RAHMAT,HUSAIN,et al.Robust precision control for a class of electro-hydraulic actuator system based on disturbance observer[J]. International Journal of Precision Engineering & Manufacturing, 2015,16(8):1753-1760.
[20] 孙文娟. 自适应遗传算法的改进及其在爆炸冲击响应谱时域合成优化中的应用研究[D].合肥:中国科学技术大学,2019.
SUN Wenjuan.Improvement of adaptive genetic algorithm and its application in time-domain synthesis optimization of explosive shock response spectrum[D].Hefei:University of Science and Technology of China, 2019:87-63.
Research on automation of support based on genetic algorithm and BP neural network
- 相关推荐

