基于局部化带全局追踪的露天煤矿边坡临界滑面确定方法研究
时间：2024-02-01 来源：中国煤炭杂志官网 分享：★ 煤矿安全 ★
基于局部化带全局追踪的露天煤矿边坡临界滑面确定方法研究
0 引言
确定边坡临界滑面的位置是露天煤矿边坡稳定性分析的关键问题，目前工程中常用的方法主要分为极限平衡法和有限元法两类。极限平衡法一般采用滑面形状为弧形或者多段型的假设，对整个露天煤矿边坡区域进行遍历搜索，计算各个假设滑面上块体的静力平衡方程，遴选出安全系数最小的滑面即为该边坡的临界滑面[1-3]。有限元法采用弹塑性本构模型计算露天煤矿边坡的应力场和位移场，通过强度折减、过载等方式使边坡达到临界状态，对有限元计算结果进行后处理，估算出滑面的位置。
目前，用于判断露天煤矿边坡失稳破坏的判据主要有3种：数值解非收敛判据[4]，以静力平衡计算不收敛作为边坡整体失稳的标志；塑性区贯通判据[5]，以塑性区或某一幅值的等效塑性应变由坡脚至坡顶贯通作为边坡整体失稳的标志；位移突变判据[6]，以土体内某些点的应变和位移发生突变且无限发展作为边坡整体失稳的标志。
确定临界滑动面空间位置的方法包括：基于畸变网格或贯通的塑性应变等色图[4，7]；沿深度方向搜索最大塑性应变、最大剪应变增量、最大位移变化率位置[8-10]；求解滑动面控制方程[11-12]；对边坡位移及节点安全系数聚类[13]。
与极限平衡法相比，有限元法考虑岩土体变形协调条件与本构关系，可以模拟露天煤矿边坡渐进破坏过程，能够更好地适用于各种复杂工况条件。然而，有限元法中边坡失稳状态的判识与临界滑面的确定通常互相割裂，彼此之间缺乏内在关联。为此，提出一种局部追踪算法[14]，通过追踪局部化带形成、扩展、汇合直至贯通的过程，在判断边坡的极限平衡状态的同时，确定临界滑动面的位置。局部追踪算法在处理单条局部化带扩展时十分简单，但在处理多条局部化带扩展时非常繁杂，缺少鲁棒性，并且构造的局部化带路径也不光滑。
为解决上述问题，引入OLIVER J等[15-16]提出的全局追踪算法(Global Tracking Algorithm)，结合局部化带贯通判据，发展一种基于全局追踪算法的露天煤矿边坡临界滑面确定方法，并通过算例分析验证了临界滑面确定方法的有效性。
1 材料失效理论与边坡失稳判据
1.1 材料失效理论
局部化带理论[17-18]认为，土体材料失效表现为由原先光滑、连续化的变形模式转变为以剧烈变形狭窄条带形式出现的、高度局部化的变形模式。如图1所示，当土体材料出现剧烈变形的局部化带时，位移率在跨越局部化带时保持连续，而位移梯度率出现间断，即：
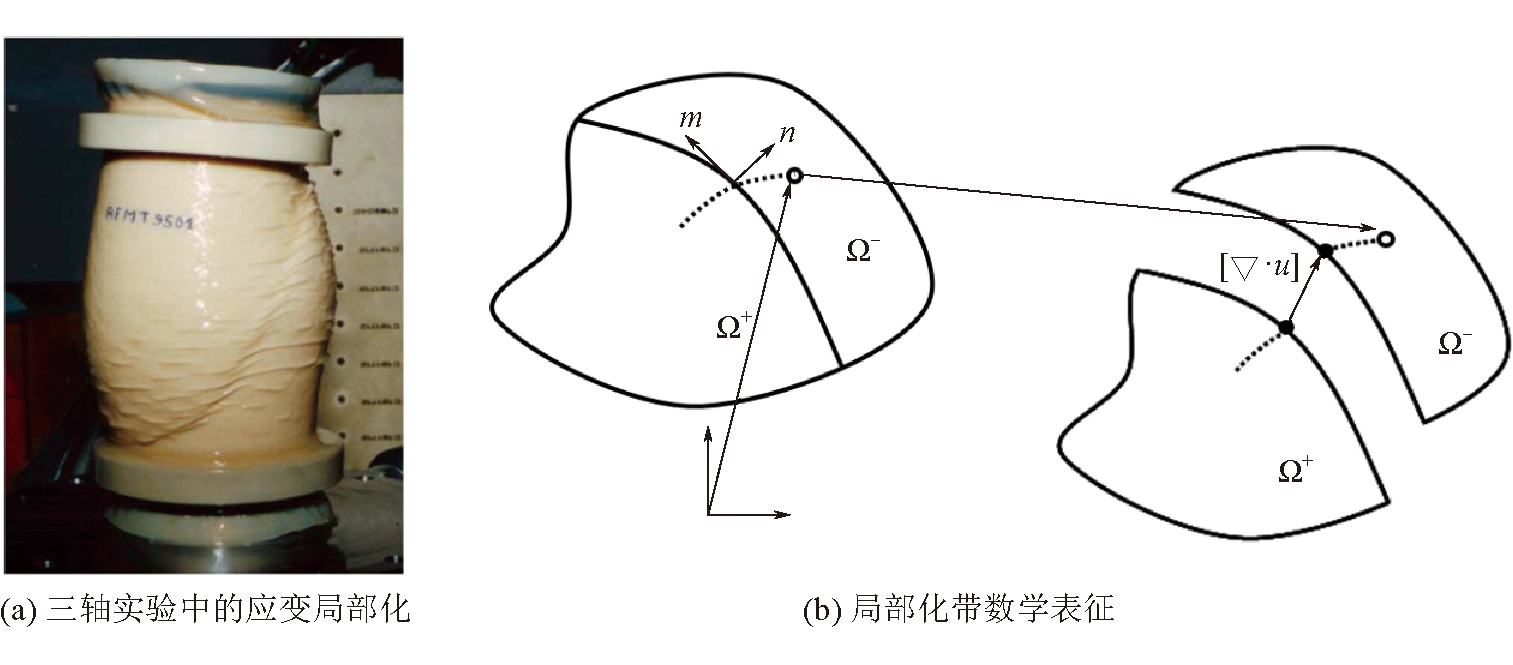
图1 土体材料应变局部化现象
∇˙
∇˙
(1)
式中：∇˙
位移梯度率；
“+”“-”——带状区域的正表面和负表面；
n——局部化带的单位法向量；
m——局部化带的单位切向量；
局部化带两侧速度间断。
1.2 边坡失稳判据
在局部化带理论框架下，边坡失稳破坏过程可以看作土体单元不断发生局部化失效的过程。坡体内部局部化带演化如图2所示。
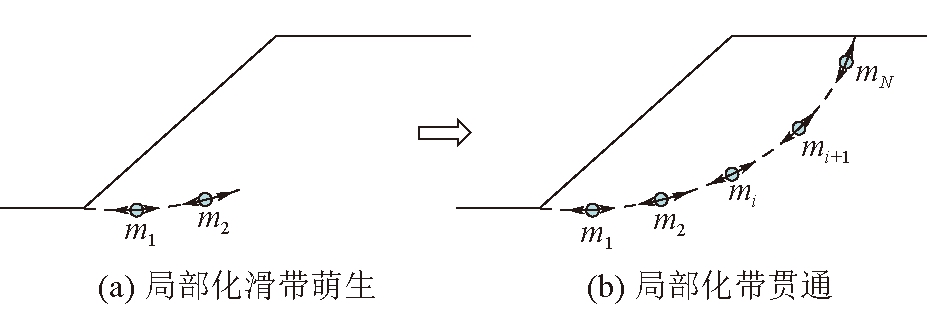
图2 坡体内部局部化带演化
由于边坡内材料的非均匀性、初始弱面的存在以及非均匀分布的荷载与边界约束，边坡内部的应力场始终是不均匀的，一些应力集中单元率先发生实现，形成局部化带。随着外部荷载的增加、材料强度的减小以及土体单元实现后释放载荷在边坡内部的转移和调整，新的局部化带不断形成，已有的局部化带继续扩展、汇合，直至在坡体内部完全贯通。在此极限状态，处于局部化的土体单元沿其局部化带滑移方向除承担与其强度相适应的载荷之外，已无能力承担附加荷载，任何微小的扰动都可能导致滑体沿连续贯通的局部化带发生大变形，最终引发边坡模型的整体失稳。
因此，可将局部化带由坡底至坡顶的完全连续贯通时刻定义为边坡力学模型的极限平衡状态，将局部化带的贯通路径定义为边坡模型的临界滑动面。只要准确地追踪到局部化带自萌生至贯通的完整路径，即可同时确定边坡模型的极限状态和滑动面位置。
2 局部化带追踪技术
2.1 局部化信息
为准确追踪局部化带路径、确定边坡临界滑面，需要发展有效的追踪技术，即根据每个时间步边坡有限元计算结果，通过局部化带追踪算法，以后处理的方式再现边坡内部局部化带的演化状态与扩展路径。在局部化带理论框架下，从边坡有限元计算结果中提取追踪算法所需的两类信息。
(1)输入信息1：局部化单元。当有限元单元满足局部化失稳条件时，该单元属于局部化单元集合
局部滑带将贯穿该单元。根据局部化带理论[17-18]，有限元单元发生局部化失稳的临界条件为：
(2)
式中：
局部化单元
中心点的切线刚度张量；
局部化单位法向量。
(2)输入信息2：局部化扩展方向。对于局部化单元
局部化带在该单元中的扩展方向由局部化向量
决定。为单位切向量，与式(2)中的局部化单位法向量
正交，即：
(3)
考虑到满足式(2)的解不唯一，当有限元单元发生局部化失稳时，至少存在2组潜在的局部化扩展方向。本篇采用“沿实际局部化带切线方向，绝对位移率分量最大”原则，从多个候选局部化向量中选取局部化带的实际扩展方向，其数学表达式为：
(4)
式中：
局部化单元的位移增量；
局部化带潜在的扩展方向。
2.2 追踪算法
在数值实现时，边坡有限元将整个边坡离散为一组单元的组合体，将连续的无限自由度问题变成离散的有限自由度问题。由于单元内部的应力场被平均化处理，由单元积分点(高斯点)的应力近似代表，因此对于满足式(2)的局部化单元，局部化带出现的位置是不确定的，可以出现在局部化单元的任意区域。
为此，发展了局部追踪算法(Local Tracking Algorithms)和全局追踪算法(Global Tracking Algorithms)来确定局部化带的具体扩展路径。这两类算法均遵循如下假定条件：局部化带以离散线段形式在每个局部化单元中扩展；局部化带在相邻单元扩展时，要求保持连续性。
2.2.1 局部追踪算法
根据前文给出的局部化信息，局部追踪算法从根单元出发，逐个单元地追踪局部化带扩展路径。局部追踪算法示意如图3所示。
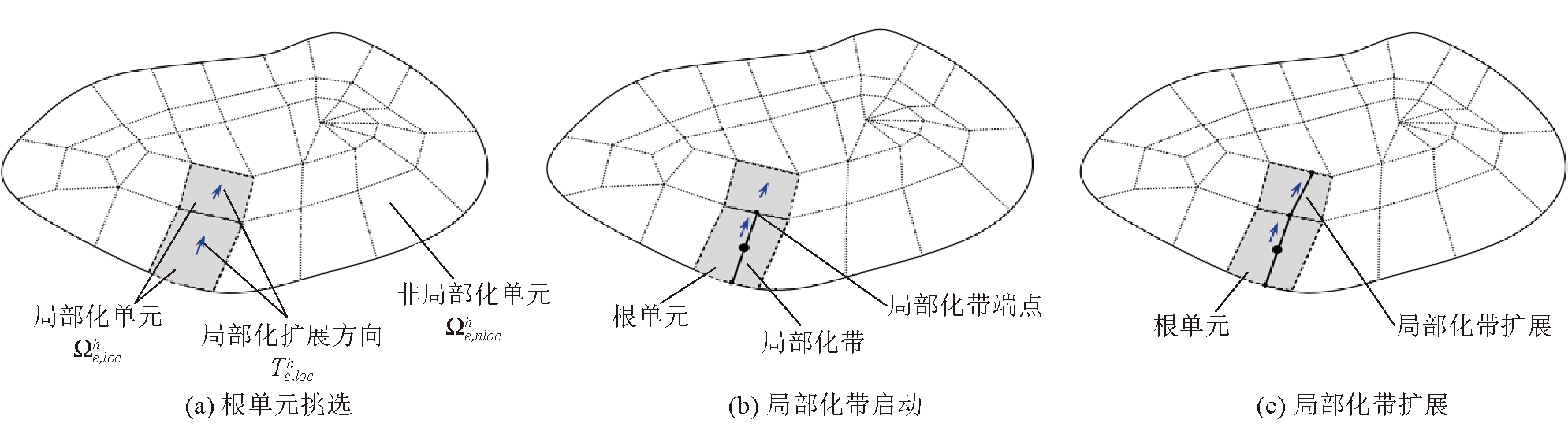
图3 局部追踪算法示意
局部追踪算法基本流程如下所示。
(1)根单元挑选。从局部化单元集合中挑选出最早进入局部化的单元，将其定义为根单元，如图3(a)所示。
(2)局部化带启动。从根单元的中心点出发，局部化带沿局部化扩展方向扩展至单元边界，如图3(b)所示。
(3)局部化带扩展。核查局部化带端点两侧单元是否为局部化单元，如果是，从局部化带端点出发，继续沿对应单元的局部化扩展方向扩展局部化带，直至到达边界或局部化带端点两侧单元为非局部化单元，如图3(c)所示。
局部追踪算法在处理单条局部化带扩展时十分简单，但在处理多条局部化带扩展时非常繁杂[14-16]，缺少鲁棒性，并且构造的局部化带路径也不光滑。
2.2.2 全局追踪算法
全局追踪算法将局部化带路径追踪问题转换为求解稳态热传导类问题，由等温线获得所有潜在局部化带，从中确定局部化带扩展路径，如图4所示。
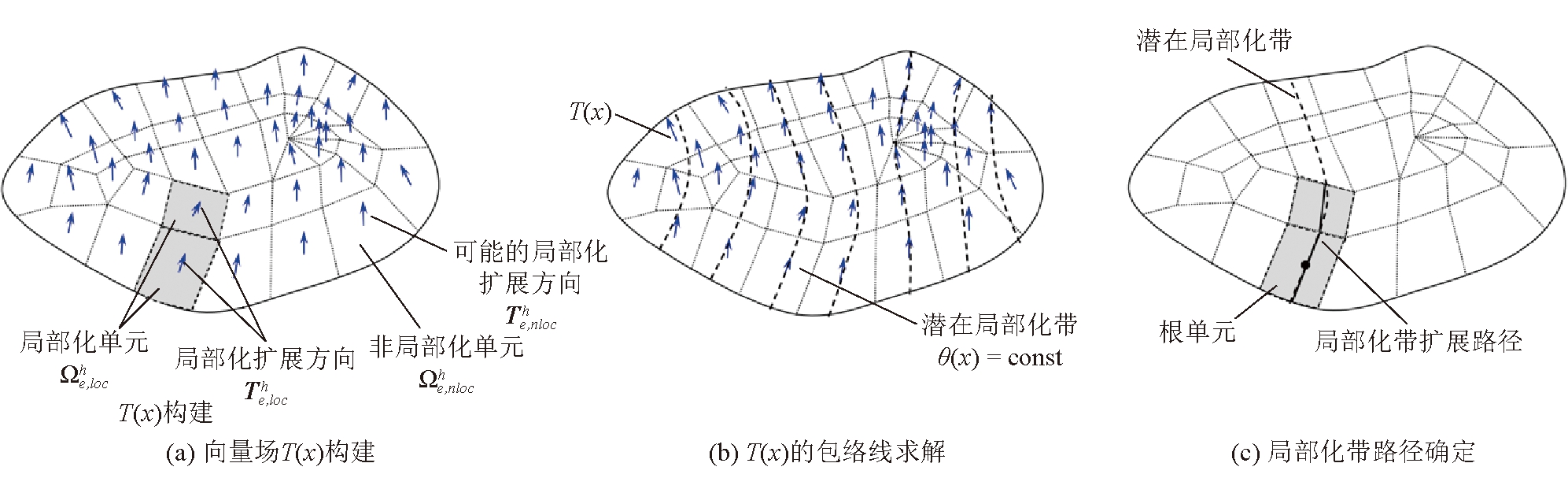
图4 全局追踪算法示意
全局追踪算法分为3个部分：
(1)构建向量场T(x)。全局追踪算法不仅需要局部化单元中局部化扩展方向信息
而且需要非局部化单元中可能的局部化扩展方向信息
构建由所有扩展方向组成的向量场
如图4(a)所示。
输入信息3：可能的局部化扩展方向。对于未进入局部化的单元
可能的局部化扩展方向
定义为：
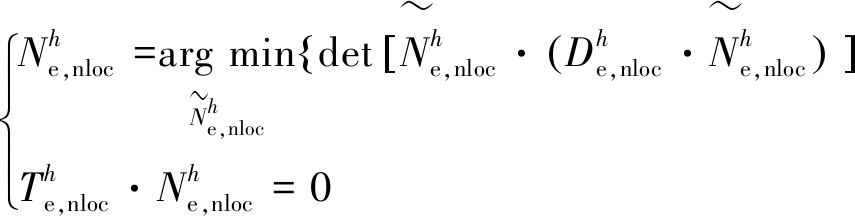
(5)
式中：
非局部化单元
中心点的切线刚度张量；
可能的局部化单位法向量。
(2)求解向量场T(x)的包络线(潜在局部化带)。边坡内部的局部化带可以看作无厚度的曲线集合{Si}，曲线Si上任意坐标x处的切线方向为局部化扩展方向T(x)。因此，从数学角度看，追踪局部化带路径等同于求解向量场T(x)的包络线。
在边坡区域Ω内定义标量函数θ(x)，使其梯度与T(x)始终正交，即：
T(x)·∇θ(x)=0 x∈Ω
(6)
考虑到函数θ(x)的等值线(θ(x)为常数)垂直于梯度∇θ(x)，可知θ(x)的等值线即为向量场T(x)的包络线，物理上代表所有潜在局部化带，如图4(b)所示。
为了求解θ(x)，在式(6)等号两边同乘T(x)，将式(6)扩展为一组热传导类偏微分方程组，即：
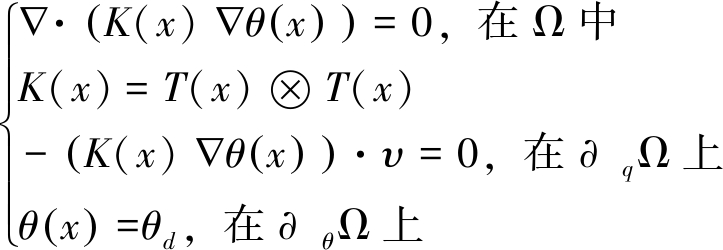
(7)
式中：υ——垂直于∂qΩ的单位向量；
θd——在Dirichlet边界条件上的值。
为获得θ(x)的非零解，应至少对位于不同等值线上的2个节点设置θd。并且，考虑到K(x)存在奇异性，需要将式(7)中的K(x)=T(x)⊗T(x)修正为：
K(x)=T(x)⊗T(x)+∈I
(8)
式中：I——单位张量；
∈——数值很小的各项同性热导率。
式(7)表明，标量函数θ(x)可以类比为温度场，-(K(x)∇θ(x))为热通量，K(x)为各向异性热传导张量。因此，追踪局部化带路径问题转变为求解无内部热源和零热通量输入的稳态热传导类问题，通过求解温度场的等温线，获得所有潜在局部化带。
(3)确定局部化带扩展路径。在获得所有潜在局部化带后，需要从中确定局部化带扩展路径。从未追踪的局部化单元集合中挑选出最早进入局部化的单元(根单元)，将通过根单元中心点的等温线标记为潜在局部化带，如图4(c)所示。追踪与潜在局部化带相交的所有局部化单元，将其标记为已追踪局部化单元，将潜在局部化带与这些局部化单元的相交线段标记为局部化带扩展路径。
如果局部化单元集合中仍然存在未被追踪的局部化单元，则继续从未追踪的局部化单元中挑选下一个根单元，开始下一条局部化带路径追踪，直至所有局部化单元均已追踪完毕。
3 边坡临界滑面判识流程
与局部追踪算法相比，全局追踪算法理论推导严密，更适合于多局部化带路径追踪问题。因此，可以基于全局追踪算法来判识边坡临界滑面，具体实施流程如下。
(1)作为后处理程序，边坡临界滑面判识程序在每个或每几个时间步结束后调用，通过追踪当前荷载下局部化带扩展路径来判识边坡滑面状态。
(2)遍历所有单元的中心点
根据式(2)提取局部化单元集合
如果
集合为空，则退出边坡临界滑面；否则，根据式(4)和式(5)，构建由局部化扩展方向信息
和可能的局部化扩展方向信息组成的向量场
同时，建立(0，tn](tn为当前计算时间步)加载时间段内、局部化单元首次进入局部化的时间集合
(3)采用与边坡模型相同的有限元网格，根据式(7)及向量场
计算各单元中心点热传导张量K(x)，数值求解热传导类边界值问题，获得所有节点的温度场。
(4)遍历所有局部化单元集合将其标记为未追踪状态，并对单元节点求平均温度，建立局部化单元中心温度集合
物理上，经过每个局部化单元中心的等温线都可看作一条潜在局部化带。
(5)遍历所有处于未追踪状态的局部化单元，从集合
中寻找最早进入局部化的单元(根单元)，将通过根单元中心的等温线
标记为潜在局部化带。追踪与潜在局部化带相交的所有局部化单元，将这些单元标记为已追踪状态，将潜在局部化带与这些局部化单元的相交线段标记为局部化带扩展路径。
(6)核查局部化单元是否全部标记为已追踪状态。如果不是，转步骤(5)，开始下一条局部化带路径追踪。如果是，则完成全部局部化带路径追踪。
(7)根据各条局部化带路径，判断局部化带贯通情况。如果某条局部化带由坡底至坡顶完全连续贯通，则整个边坡处于极限平衡状态，该条局部化带扩展路径为临界滑面，边坡稳定性计算结束；如果没有，则转步骤(1)，开始下一个时间步长加载及边坡稳定性计算。
4 有限元数值实现
全局追踪算法的数值实现流程：使用边坡有限元模型网格，将给定的边坡区域Ω离散为nelem个有限单元和nnode个有限节点。采用有限元方法将稳态热传导控制方程(7)离散化[19]，导出其对应的离散形式，即：
寻找：
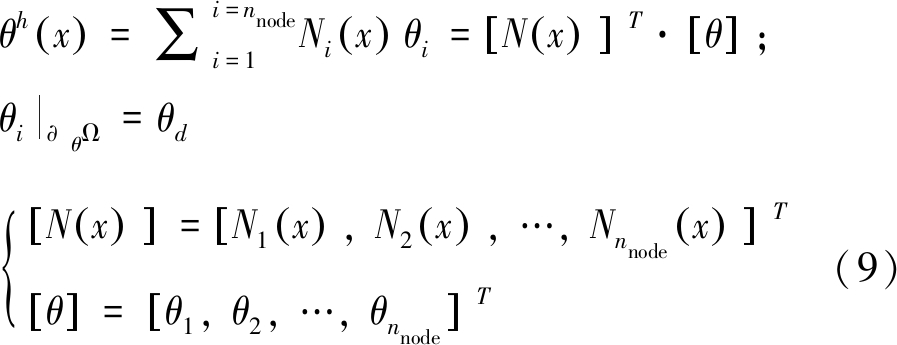
以致：
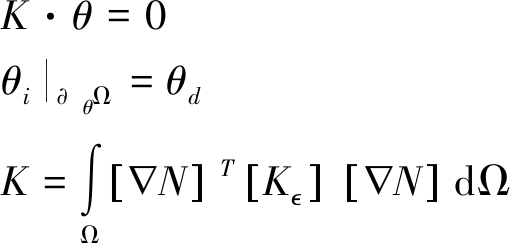
(10)
式中：Ni(x)——标准形函数；
K——相应的刚度矩阵。
作为后处理程序，式(10)需要在边坡稳定性计算的每个或每几个时间步完成后调用，并且根据前文描述的追踪算法判识边坡临界滑面来确定每个局部化单元中局部化带的具体扩展位置，见步骤(4)～(7)。
需要注意的是，如果未指定边界温度(∂θΩ=Ø⟹∂qΩ=∂Ω)，则K矩阵的秩为nnode-1。因此，必须在至少一个节点处指定温度，以确保有限元方程(10)具有唯一解。此外，为了避免温度场θ出现常数解(这将无法区分不同的等温线)，应在另一个节点处指定温度。如何指定温度值不影响局部化带位置的判定，只要不在同一条等温线上的2个点上施加2种不同的温度值即可。
5 算例验证
为验证全局追踪算法的有效性，分别采用强度折减和位移加载方式，开展两类边坡临界滑面追踪数值分析。土体材料均为理想弹塑性材料，屈服准则为平面应变条件下摩尔-库仑结合DP准则(DP4准则)。
5.1 算例1：强度折减
采用文献[4，14]中的边坡算例：边坡坡高H=20 m，坡角β=26.57°，杨氏模量E=100 MPa，泊松比v=0.3，容重γ=20 kN/m3，黏聚力c=10 kPa，内摩擦角φ=20°。土体材料为理想弹塑性材料，强度准则采用平面应变条件下摩尔-库仑结合DP准则(DP4准则)。算例1边坡尺寸及网格划分如图5所示，边坡左、右两侧边界为法向约束，底边为双向固定约束，共划分四边形单元5 686个、节点5 878个。采用有限元强度折减方法，按照c/ω，tanφ/ω方式不断折减土体材料强度参数，模拟边坡渐进破坏过程及其位移场演化信息，直至边坡发生整体失稳。其中，ω为折减系数，其初始值ω0=1.0，步长△ω=0.002。
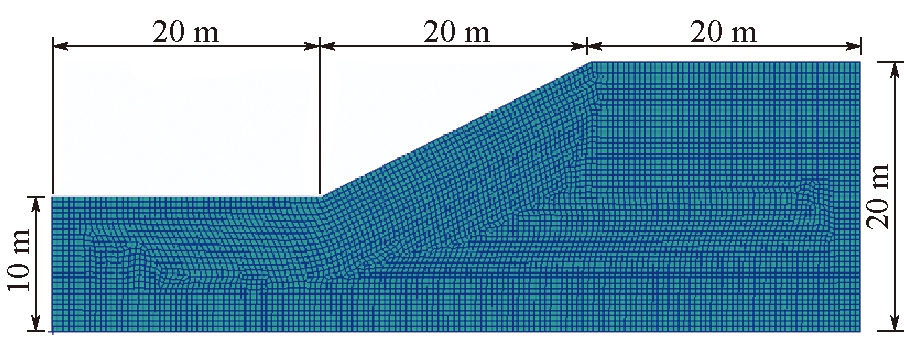
图5 算例1边坡尺寸及网格划分
折减系数ω=1.384时等效塑性应变云图如图6所示。由图6可以大致确定滑动面的分布范围，但无法精确定位。
图6 折减系数ω=1.384时等效塑性应变云图
采用文献[12]中局部追踪技术，折减系数ω=1.384时局部化带扩展路径如图7所示[12]。由图7可以看出，局部追踪技术给出的局部化区域要比塑性云图的范围小得多，主要集中在边坡的局部破坏区域。然而在坡角及坡肩附近，多条局部化带相互交织，并不光滑，这给临界局部化带位置的判识带来了困难。此外，这些局部化滑带宽度与有限元网格尺寸相关，通常占据2～3个单元。
图7 折减系数ω=1.384时局部化带扩展路径
折减系数ω=1.384时，采用全局追踪技术获得的温度场等值线和局部化带扩展路径如图8所示。与局部追踪技术相比，全局追踪技术同时利用局部化单元的扩展方向和非局部化单元可能的扩展方向求解边坡向量场的包络线，从而从所有潜在局部化带中确定局部化带扩展路径。这种方法追踪滑面的鲁棒性更高，不仅主级滑面(红色线条)为无厚度的光滑曲线，次级滑面(蓝色线条)清晰，而且各级滑面之间以层状方式平行分布，不再出现滑面彼此交叉的情况。
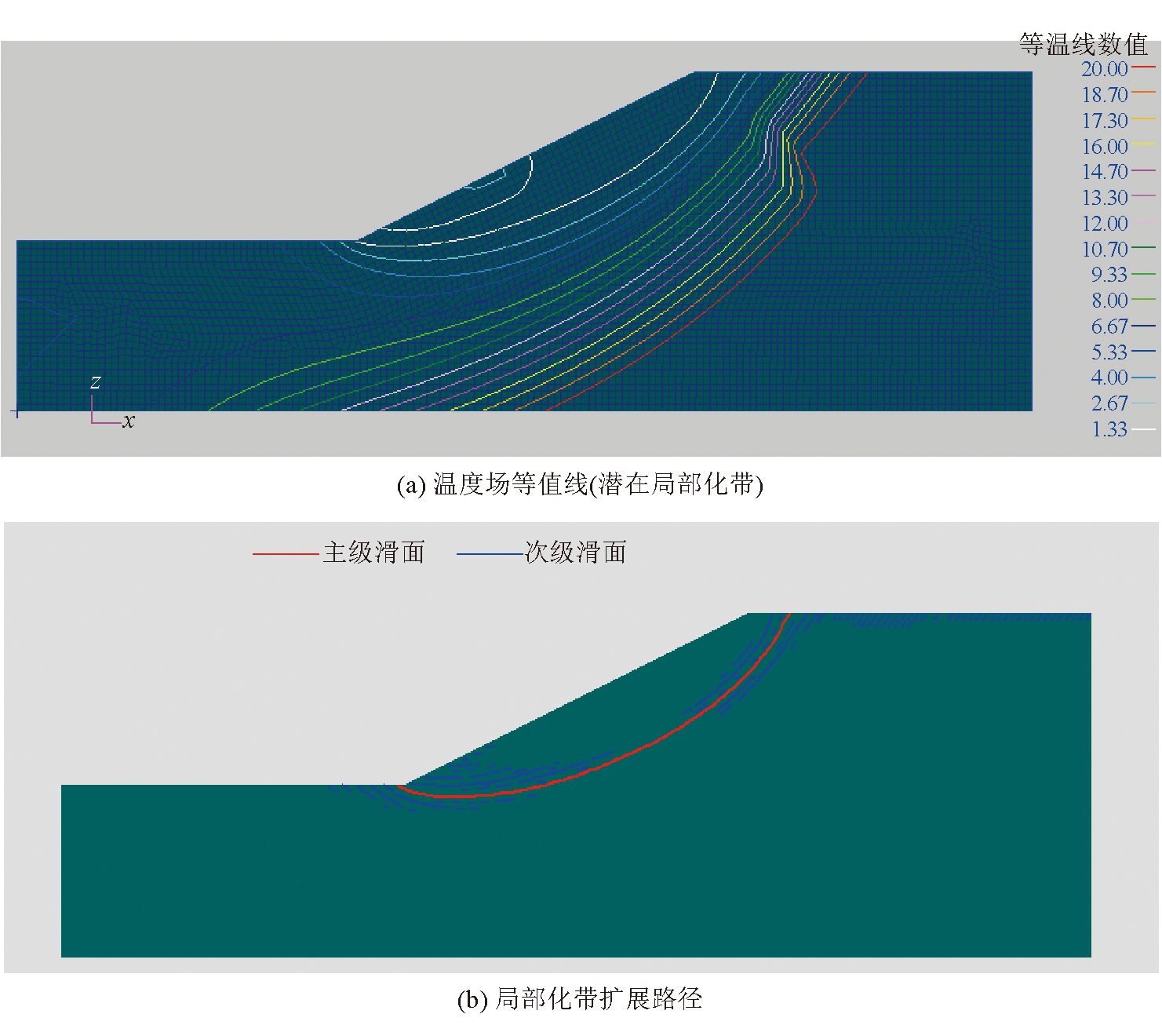
图8 折减系数ω=1.384时采用全局追踪技术追踪效果
通过以上对比可以看出，借助塑性应变云图的传统临界滑动面确定方法具有很大的局限性，仅能大致确定滑动面的分布范围；局部追踪技术虽然能够给出更具体的局部化区域，但在坡角及坡肩附近的局部化带相互交织，影响了临界局部化带位置的判识；而全局追踪技术则能够克服这些问题，提供更准确、更全面的局部化带扩展路径信息。
5.2 算例2：位移加载
采用文献[14，20]中的边坡算例：坡高H=10 m，坡角β = 45°，杨氏模量E = 10 MPa，泊松比v = 0.4，容重γ= 20 kN/m3，黏聚力c = 20 kPa，内摩擦角φ= 30°。边坡几何尺寸及网格划分如图9所示，边坡右侧边界为法向约束，底边为双向固定约束。除重力载荷G外，边坡在坡顶承受竖直向下位移u作用，F为竖向位移u产生的竖向反力。重力载荷通过初始应力场体现，所产生的位移不计入竖向位移u中。
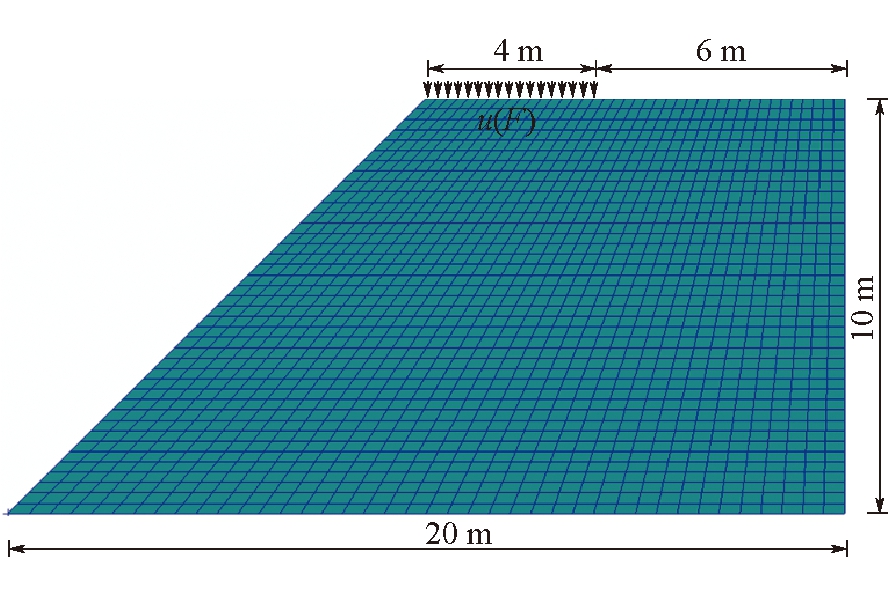
图9 算例2边坡几何尺寸及网格划分
边坡在失稳临界状态下(竖向位移u=0.14 m)的等效塑性应变云图、采用局部追踪技术和全局追踪技术获得的局部化带扩展路径如图10～12所示。由图10～12可以看出：通过塑性应变云图呈现出2条条带状分布的贯通滑动面，无法准确判断临界滑动面的位置；局部追踪技术和全局追踪技术都能够判断临界滑动面的位置；然而，局部追踪技术给出的临界滑面不够准确，其路径不光滑，且在坡体下半区域内的局部滑带也呈现出条带状分布，占据了2～3个单元的厚度；与局部追踪技术相比，全局追踪技术追踪的主级滑面(红色线条)以无厚度的光滑曲线的方式呈现，没有出现滑面互相交叉以及滑面条带化的情况，因此，全局追踪技术可以为后续的边坡工程治理提供更有效地支撑。
图10 u=0.14 m时等效塑性应变云图
图11 u=0.14 m时局部化带扩展路径
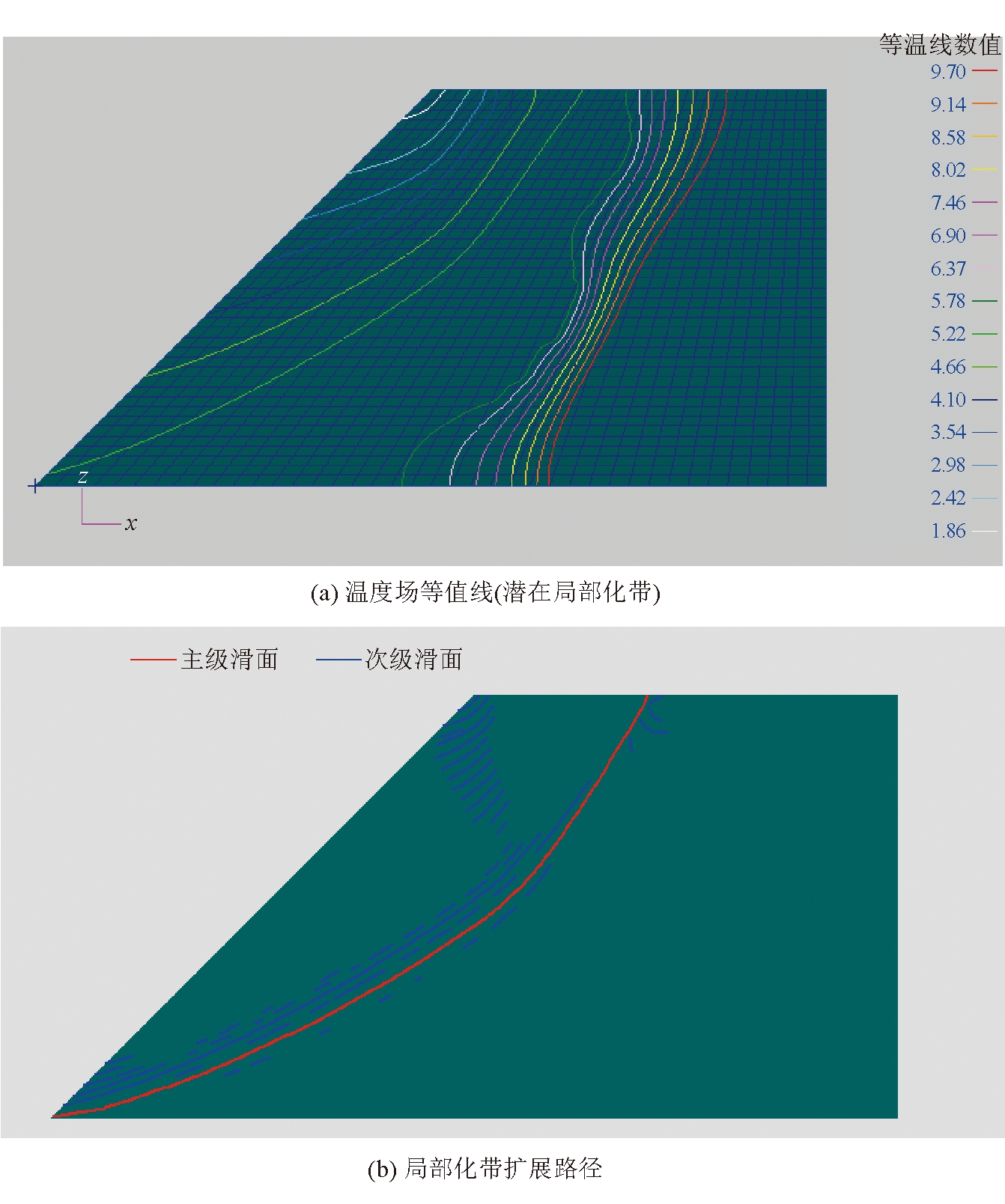
图12 u=0.14 m时采用全局追踪技术追踪效果
通过对比分析，可以得出全局追踪技术在追踪边坡滑动面方面具有更高的鲁棒性和准确性，能够以光滑曲线的方式呈现局部化带路径，克服了传统方法和局部追踪技术的局限性，从而为后续的边坡工程治理提供了重要的分析支撑手段。
6 结论
(1)在局部化带理论框架下，将全局追踪算法与局部化带贯通判据相结合，提出了一种基于全局追踪技术的露天煤矿边坡临界滑面确定方法。该方法将追踪局部化带路径的问题转化为求解无内部热源和零热通量输入的稳态热传导问题，通过追踪经过局部化单元中心的等温线来辨识局部化带路径的扩展及贯通状况。
(2)算例结果比对分析表明：借助塑性应变云图的传统临界滑动面确定方法存在很大的局限性，只能大致确定滑动面的分布范围，而无法准确定位；局部追踪技术虽然能够给出更具体的局部化区域，但局部化带经常相互交织，影响了临界局部化带位置的精准判识，此外，局部追踪技术给出的临界滑面不够准确，其路径不光滑，经常呈现出条带状分布特点；基于全局追踪技术的边坡临界滑面确定方法具有更好的鲁棒性，它能以光滑曲线的方式呈现滑面，不会出现滑面互相交叉以及滑面条带化的情况。这种方法更适合多条局部化带同时扩展情况下的临界滑面的确定。
(3)提出的全局追踪技术结合局部化带贯通判据的方法能够有效地确定边坡的临界滑面，克服了传统方法的局限性。
[1] GRECO V R.Efficient monte carlo technique for locating critical slip surface[J].Journal of Geotechnical Engineering,1996,122(7):517-525.
[2] MALKAWI AIH,HASSAN W F,SARMA S K.Global search method for locating general slip surface using monte carlo techniques[J].Journal of Geotechnical & Geoenvironmental Engineering,2001,127(8):688-698.
[3] 杨善统,姜清辉,尹涛,等.边坡临界滑面搜索的改进粒子群优化算法[J].岩土工程学报,2015,37(8):1411-1417.
[4] GRIFFITHS D V,LANE P A.Slope stability analysis by finite elements[J].Geotechnique,1999,49(3):387-403.
[5] 栾茂田,武亚军,年廷凯.强度折减有限元法中边坡失稳的塑性区判据及其应用[J].防灾减灾工程学报,2003,23(3):1-8.
[6] WEI W B,CHENG Y M,LI L.Three-dimensional slope failure analysis by the strength reduction and limit equilibrium methods[J].Computers and Geotechnics,2009,36(1-2):70-80.
[7] 连镇营,韩国城,孔宪京.强度折减有限元法研究开挖边坡的稳定性[J].岩土工程学报,2001,23(4):407-411.
[8] 孙冠华,郑宏,李春光.基于等效塑性应变的边坡滑面搜索[J].岩土力学,2008,29(5):1159-1163.
[9] 李剑,陈善雄,余飞.基于最大剪应变增量的边坡潜在滑动面搜索[J].岩土力学,2013,34(S1):371-378.
[10] 袁维,胡叶江,李小春,等.一种基于位移场分析的临界滑动面确定方法研究[J].岩土力学,2016,37(6):1791-1798.
[11] 郑宏,刘德富,罗先启.基于变形分析的边坡临界滑动面的确定[J].岩石力学与工程学报,2004,23(5):706-719.
[12] 王东英,杨光华,姜燕,等.基于局部安全系数的边坡滑面搜索[J].广东水利水电,2020(2),79-84,88.
[13] 秦雨樵,汤华,冯振洋,等.基于聚类分析的边坡稳定性研究[J].岩土力学,2018,39(8):2977-2983.
[14] 刘晓宇,赵颖,刘洋,等.土质边坡极限平衡状态及临界滑动面的判定方法[J].岩石力学与工程学报,2012,31(7):1369-1378.
[15] OLIVER J,HUESPE A E,SAMANIEGO E,et al.Continuum approach to the numerical simulation of material failure in concrete[J].International Journal for Numerical and Analytical Methods in Geomechanics,2004,28:609-632.
[16] PARVANEH S M,Foster C D.On numerical aspects of different updating schedules for tracking fracture path in strain localization modeling[J].Engineering Fracture Mechanics,2016,152:26-57.
[17] OTTOSEN N S,RUNESSON K.Properties of discontinuous bifurcation solutions in elasto-plasticity[J].International Journal of Solids and Structures,1991,27(4):401-421.
[18] LARSSON R,RUNESSON K,STURE S.Embedded localization band in undrained soil based on regularized strong discontinuity theory and FE analysis[J].International Journal of Solids and Structures,1996,33:3081-3101.
[19] ZIENKIEWICZ O C,TAYLOR R L. The finite element method[M].Fifth edition.Oxford:Butterworth Heinemann,2000.
[20] REGUEIRO R A,BORJA R I.Plane strain finite element analysis of pressure sensitive plasticity with strong discontinuity[J].International Journal of Solids and Structures,2001,38:3647-3672.
Research on the determination method for the critical sliding surface of open-pit coal mine slopes based on localized band and global tracking
移动扫码阅读
FAN Yuchao. Research on the determination method for the critical sliding surface of open-pit coal mine slopes based on localized band and global tracking [J].China Coal，2023，49(11)：39-48.DOI：10.19880/j.cnki.ccm.2023.11.006
- 相关推荐
