矿井煤流数字孪生激光扫描质量评价方法研究
时间:2024-05-20 来源:中国煤炭杂志官网 分享:科技引领
矿井煤流数字孪生激光扫描质量评价方法研究
0 引言
近年来,煤矿智能化已成为煤炭行业基础研究和新技术研发应用的热点领域,随着大数据、人工智能、机器人、智能传感等高新技术的不断引入,我国煤矿智能化已进入全面发展阶段[1]。葛世荣等[2-3]提出了矿山数字孪生技术框架构想,面向煤矿智能化应用,发挥数字孪生连接物理世界和信息世界的桥梁与纽带作用,研究了数字孪生智采工作面系统的概念、架构及构建方法。孪生建模是数字孪生的基础和核心技术之一,采用三维激光扫描技术可以高速、高精度地获取海量被测物体的点云数据,实现被测物的动态三维创建,从而保持孪生模型的高保真、高可靠、高精度特征。
因此,激光扫描技术可用于全矿井数字孪生虚拟模型的构建,目前已有部分学者[4]将其用于地面煤场、井下巷道、设备的扫描等,但多数进行的是先验静态模型构建。胡而已等[5]前期已开展了基于激光扫描技术的煤流监测数字孪生建模研究,主要通过激光扫描技术建立井下带式输送机和刮板输送机的运煤数字模型[6],由此实时构建运输设备上部堆煤的三维物理场信息,作为煤矿主煤流系统的智能调控依据。在煤流数字孪生扫描建模中,激光点云模型直接反映了带式输送机或刮板输送机上部的煤流轮廓高度参量。由于井下激光扫描容易受到煤矿复杂工况条件的影响,激光传感器、采集及传输系统易受到干扰,终端获取的点云模型质量得不到保障,因此如何评价基于激光扫描的数字孪生建模精度成为亟待研究解决的关键问题。为了动态调参、优化点云模型质量,对劣化后的煤流点云模型进行实时模型质量评价,评估模型的失真程度,作为模型增强和算法分析比较的依据,进而为提高系统数字孪生建模精度提供支持。
根据对参考模型信息的依赖程度,模型质量评价方法主要分为无参考、半参考、全参考[7],其中全参考模型质量评价算法需要真实且不存在失真的参考模型,而半参考只要求部分真实模型信息,无参考则不需要任何真实模型信息[8-9]。在模型评价方法发展初期,Wang等[10-11]提出结构相似度方法,性能强于PSNR(Peak Signal-to-Noise Ratio)方法[12],但是该算法不能很好地评价模型的劣化程度。随着机器学习技术的发展,Mittal等人[13]提出了依据空间域下的NSS(Natural Scene Statistics)特征来构建模型质量评价的半参考模型,该方法使用GDD和AGGD模型参数作为特征,描述SVM(Support Vector Machine)特征与模型质量之间的映射关系。而在深度学习领域,Kang等[14]提出了基于CNN(Convolutional Neural Network)的NR-IQA(No Reference Image Quality Assessment)半参考模型,该模型包含1个卷积层和池化层、2个全连接层,通过线性回归最小二乘法预测质量分数。
目前基于深度学习的质量评价方法属于数据驱动的黑盒模型,不仅过度依赖样本,而且缺乏有力的理论支撑。由于井下工况环境复杂,缺少针对煤流点云的开源样本集,也无法将现有的质量评价方法直接迁移到煤流点云模型的精度评价中。因此,笔者以综放工作面后部刮板输送机运煤孪生建模为研究对象,系统研究影响煤流点云模型质量的主要因素,并提出一种适用于矿井复杂恶劣环境的数字孪生煤流点云质量评价方法,以提升放煤口煤流激光扫描孪生监测的精度,为综放工作面精准智能放煤提供科学依据。
1 煤流激光扫描数字孪生建模原理
数字孪生智采工作面是采用数据化方式构建物理工作面的虚拟模型,通过物理工作面与数字工作面的镜像反馈、数据交互分析、决策迭代优化等手段,以超现实的形式反映物理工作面的采煤流程变化,达到最优化生产配置和装备协同化开采的目的。而煤流数字孪生建模是对煤流实体进行仿真预测,通过构建动态反馈的煤流虚拟镜像,逼真模拟实际煤流运动,为数字孪生工作面提供煤流数据交互、同步反馈及煤流监控功能。
在煤矿主煤流智能输送系统中,通过激光扫描数字孪生可实现矿井全煤流智能监测。其中煤流的起始点,即采煤工作面的煤流动态孪生是整个智能化主运输系统的技术瓶颈。以综放工作面为例,应用煤流数字孪生监测可精准反映放煤口的放煤量大小和煤块颗粒度信息等,避免后部刮板输送机过载和破碎机卡阻,为转载设备及后端带式输送系统的调控预留提前量,从而提升整个主运输系统的效率和安全性。
综放工作面刮板输送机激光扫描监测模型如图1所示,该模型采用基于飞行时间的煤流监测方法,在液压支架下方、输送机侧上部安装激光雷达扫描装置,通过激光雷达的内置激光器发射红外激光,实时扫描待测煤堆表面,形成煤流实体的虚拟镜像模型,应用时间关联规则和点云配准算法,反演计算出实时输送煤堆的三维数字孪生动态模型,进而达到模拟煤流动力学运动、煤流数据同步反馈和煤流即时监控的目的。
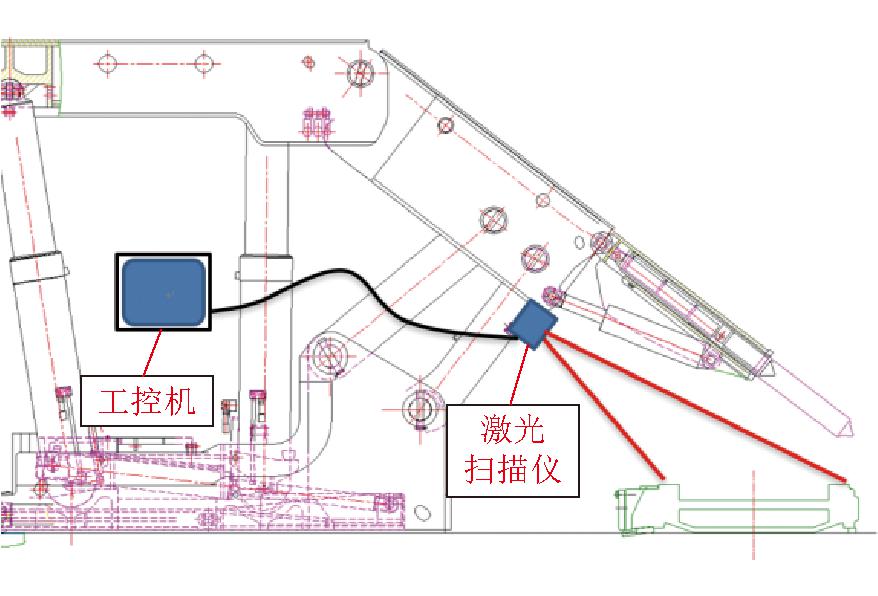
图1 综放工作面刮板输送机激光扫描监测模型
煤流数字孪生建模算法流程如图2所示,激光雷达高频扫描煤堆形貌,将反射信号解码为点云数据流。按照时间和位置关联规则,求解点云帧间的位姿变换矩阵,对连续帧点云进行拼接和配准[15],重建成煤流稀疏点云。为了抑制高频噪声、补充缺失值和剔除异常散点,利用泰勒公式、最小二乘法滤波插补和平滑点云数据[16],联系时空域关系重构为煤流稠密点云。由于算法流程中存在多个低通滤波环节,引起整个系统的群时延和相位滞后,需要根据煤流动力学原理,对煤流点云的运动趋势进行卡尔曼预测,保证煤流数字孪生模型的高保真、高可靠、高精度特征。
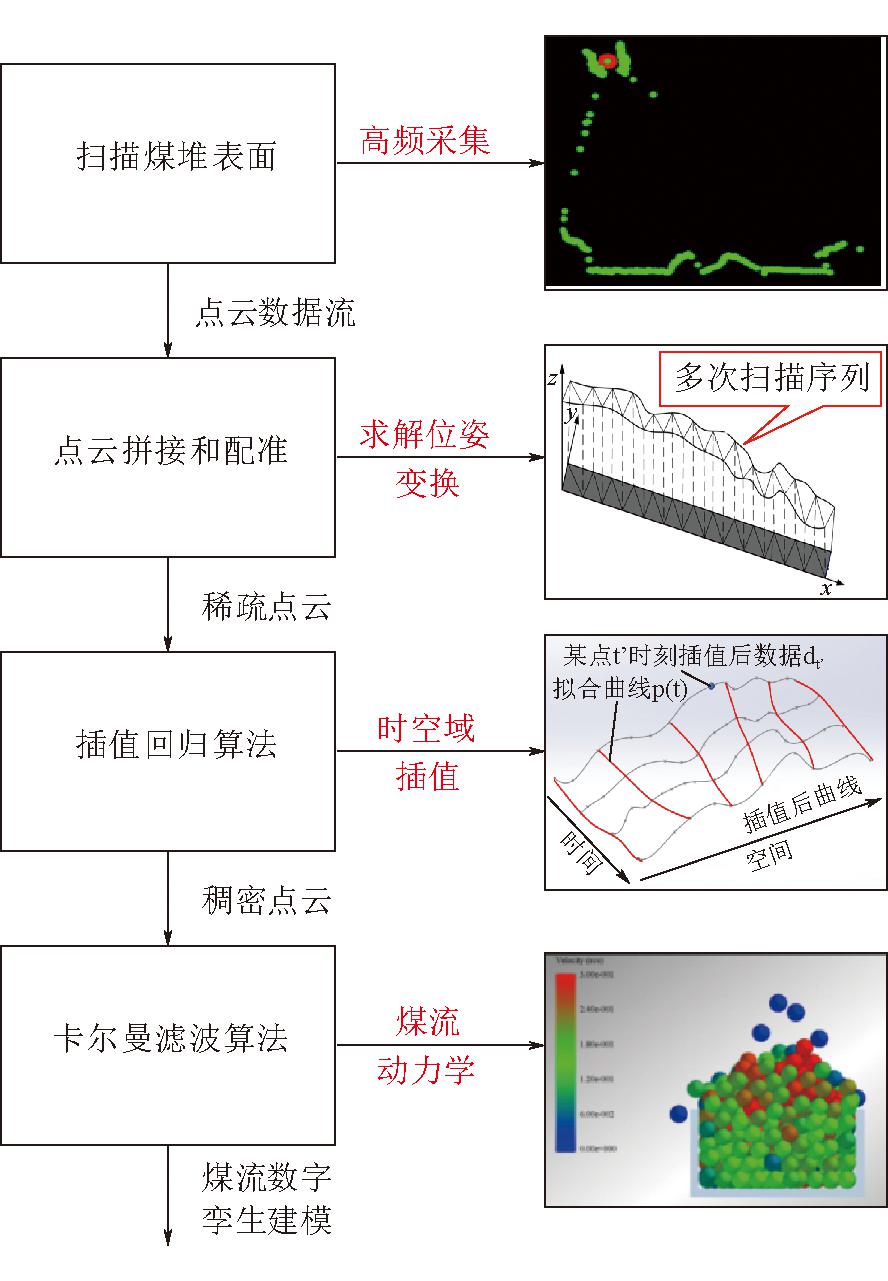
图2 煤流数字孪生建模算法流程
2 煤流点云信息熵分析
激光信噪比SINR为激光雷达物体反射强度Ps与环境噪声的反射强度Pnoise比率。物体的激光反射信号容易受到反射率、粉尘、强光等因素干扰,导致测量物体的反射强度由最大值Pmax发生衰减,物体的反射强度Ps可以由激光雷达直接测量得到,而环境噪声的反射强度Pnoise不可测,所以用Pmax和Ps的差值表示Pnoise,计算公式见式(1)和式(2):
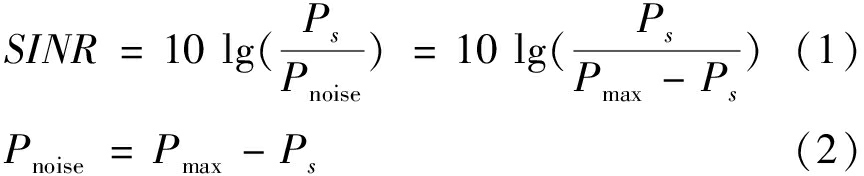
式中:SINR——激光信噪比;
Ps——激光雷达反射强度;
Pnoise——环境噪声反射强度;
Pmax——激光雷达反射强度上限。
不同环境下的激光信噪比存在差异,其中室外环境与综采工作面的信噪比差异最大,表明矿井环境中存在影响激光雷达测量精度的噪声。笔者使用的单线激光雷达型号为Sick LMS511,基本参数如下:扫描范围参考值为190°,工作距离参考值为0.7~80 m,精度参考值为±3%,角度分辨率参考值0.333°,扫描频率为50 Hz。不同环境下的激光信噪比见表1。
表1 不同环境下的激光信噪比

序号环境信噪比/dB1室外正常环境22~322综采工作面(未开机)7~123综采工作面(开机)6~104通风巷道12~265运煤巷道6~21
矿井环境下粉尘、光照、扫描角度、煤流量等因素都可能引起噪声,进而降低煤流点云的建模质量。若能够精准评价各影响因素对模型的干扰强度,量化模型的失真程度,可为动态调参优化点云模型质量奠定基础。
2.1 投影平面的信息熵分析
信息熵是一种能有效量化点云噪音强弱的指标。通常情况下,信息熵是一种标定系统信息含量的指数,系统的不确定度越高,信息熵越大。信息熵的表达式见式(3):
(3)
式中:M——系统;
H(M)——系统M的信息熵;
m——系统中的单个事件;
p(m)——事件m的发生概率。
对于包含了噪声的点云而言,噪音强度越大,点云的几何参数分布越离散,信息熵也就越大。如式(4)所示,在真实点云I(x,y,z)中引入噪声强度为σnoise的噪声G(x,y,z),可形成测量点云I′(x,y,z),其中噪声强度的取值范围为[0,1]。
I′(x,y,z)=I(x,y,z)+σnoise·G(x,y,z)
(4)
式中:I′(x,y,z)——测量点云;
I(x,y,z)——真实点云;
σnoise——噪声强度;
G(x,y,z)——点云噪声。
由于高斯混合模型(Gaussian Mixture Model,GMM)可以任意精度正逼近实数的非负黎曼可积函数[17],因此环境噪声G(x,y,z)概率密度函数可被GMM模型无限逼近,本质上矿井环境噪声就是多种高斯噪声的加权和。环境噪声的混合高斯模型描述见式(5):
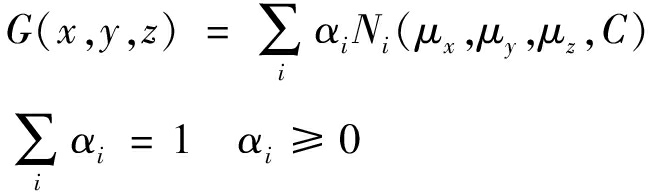
(5)
式中:αi——第i个高斯分布权重;
Ni——第i个高斯分布;
μx——高斯分布x轴均值;
μy——高斯分布y轴均值;
μz——高斯分布z轴均值;
C——协方差矩阵。
因此,只需研究混合高斯噪声对煤流点云的影响,就可模拟矿井环境下煤流点云分布情况。噪音强度不同的煤流点云分布如图3所示。
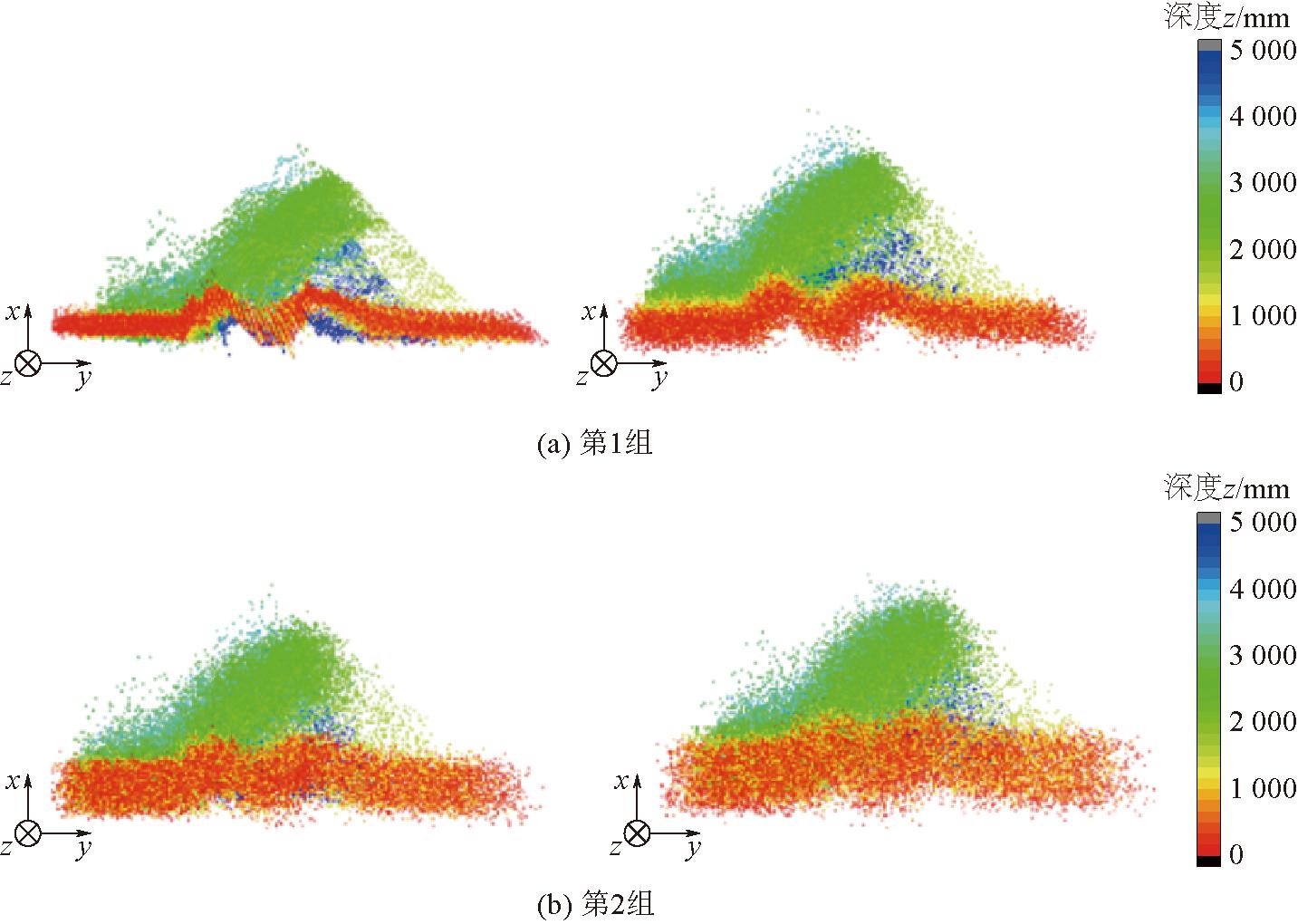
图3 噪音强度不同的煤流点云分布
由图3可以看出煤流点云中引入噪声强度不同的混合高斯噪声,点云的不同颜色代表了不同的深度z。分析结果可知,随着噪声强度的提高,点云的轮廓更加模糊,几何分布更加离散。
为了进一步了解点云分布变化,将测量点云I′(x,y,z)投影到xoy平面上,考量点云在xoy平面的分布情况。不同噪声强度下点云在xoy平面分布如图4所示。
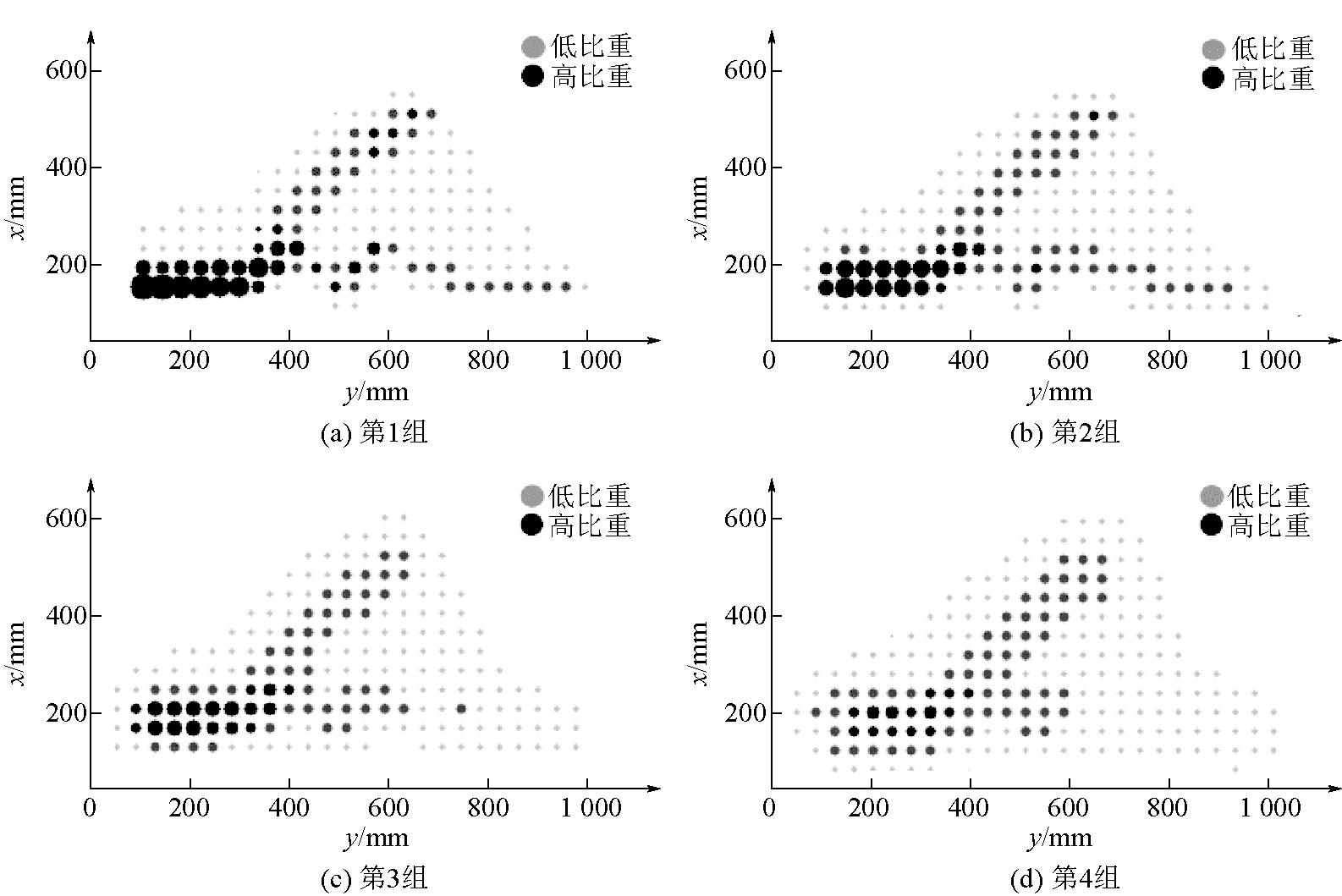
图4 不同噪声强度下点云在xoy平面分布
由图4可以看出,不同噪声强度的点云在xoy平面的分布情况,xoy平面被均分为多个区域,圆点的大小和颜色则反映了该区域点云占总数的比重。每个区域被投影到越多的点,占总数量的比重越大,圆点越大,颜色越深。对测量点云I′(x,y,z)在xoy平面的分布进行信息熵的计算见式(6):
(6)
式中:![]() 测量点云xoy面信息熵;
测量点云xoy面信息熵;
p(x,y)——点云在(x,y)的分布概率。
通过计算可得,图4(a)~(d)中的信息熵分别为4.60、4.87、5.01、5.18,结果表明噪声G(x,y,z)为混合高斯噪声时,信息熵随着噪声强度增大而增大。
2.2 法线分布的信息熵分析
点云信息熵既要反映整体趋势,又要描述细节变化。xoy面信息熵表征点云空间分布情况,却忽视了细节变化。而法线信息熵,可以很好说明点、面间的关系,是对点云信息熵细节变化的补充。
环境噪声同样会对点云的法线参数分布有影响。对噪声强度不同的点云分布进行法线估计[18],统计其法线分布并进行信息熵的计算。可以看出噪声强度越高,法线越散乱。点云法线估计如图5所示,其中白色细线为其估计法线。

图5 点云法线估计
法线分布信息熵的表达式见式(7):
(7)
式中:N——点云法线的集合;
H(N)——点云法线信息熵;
n(x,y,z)——点(x,y,z)的法向量;
p(n(x,y,z))——n(x,y,z)的法向量占总数的比重。
通过式(7)计算,可得不同噪声强度下点云法向量分布的信息熵变化情况,图5(a)~(d)的信息熵分别为5.56、5.91、6.05、6.16。结果表明,随着噪声强度的增大,点云法向量分布的信息熵越来越高。
综上,实验表明噪声强度与激光点云几何参数分布的信息熵呈正相关,可用于激光点云模型的噪音强度预测。
3 基于信息熵的噪音强度预测
3.1 多因素方差分析
由于噪声强度与点云信息熵呈正相关,点云信息熵的高低能够反映噪音强度的大小,可用于点云模型质量评价。但影响信息熵变化的因素较多,直接使用信息熵预测噪音强度,会造成结果偏差。因此,需要分析环境中其他因素对点云信息熵的影响。
在实验室环境下对煤堆进行多次激光扫描,开展多因素方差试验分析[19],充分考虑激光的扫描角度、光照强度、输送机速度、粉尘浓度、煤流量等变量,探究多种因素对点云信息熵的影响。扫描角度特指激光雷达扫描中线与输送机平面所成的入射角。
本实验的因变量为点云模型xoy面的信息熵,将扫描角度、光照强度、输送机速度、粉尘浓度以及煤流量等变量分为A、B、C、D、E这5组,为五因素四水平,选用的正交表为L16(45),显著性水平为0.05。按照表3给出的五因素四水平进行正交实验设计,按正交表L16(45)筛选出16个具有代表性的实验组合见表4,分别进行信息熵的测定,每个组合重复测量3次。
表3 水平因素

水平扫描角度(A)/(°)光照强度(B)/lux输送机速度(C)/(m·s-1)粉尘浓度(D)/(mg·m-3)煤流量(E)/(m3·s-1)122.50.10.50.50245.010.01.02.50.1372.550.01.55.00.5490.0150.02.07.51.0
表4 正交实验
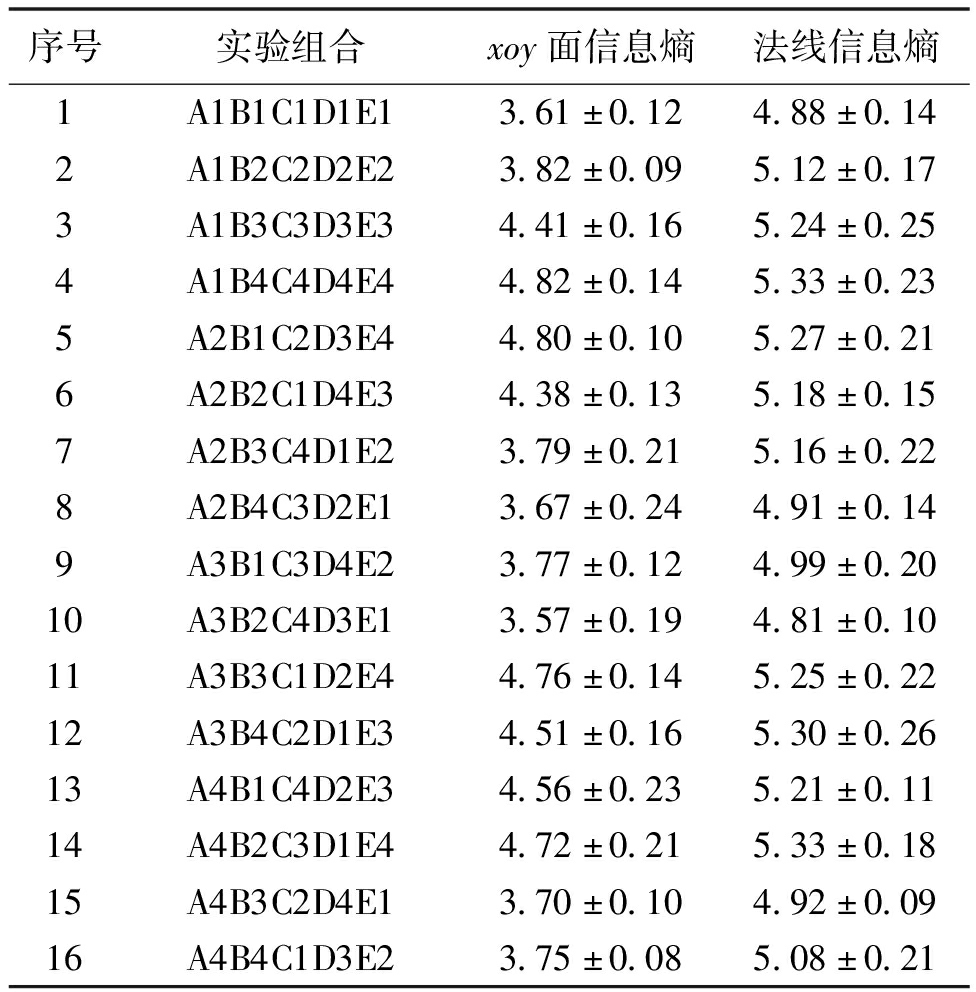
序号实验组合xoy面信息熵法线信息熵1A1B1C1D1E13.61±0.124.88±0.142A1B2C2D2E23.82±0.095.12±0.173A1B3C3D3E34.41±0.165.24±0.254A1B4C4D4E44.82±0.145.33±0.235A2B1C2D3E44.80±0.105.27±0.216A2B2C1D4E34.38±0.135.18±0.157A2B3C4D1E23.79±0.215.16±0.228A2B4C3D2E13.67±0.244.91±0.149A3B1C3D4E23.77±0.124.99±0.2010A3B2C4D3E13.57±0.194.81±0.1011A3B3C1D2E44.76±0.145.25±0.2212A3B4C2D1E34.51±0.165.30±0.2613A4B1C4D2E34.56±0.235.21±0.1114A4B2C3D1E44.72±0.215.33±0.1815A4B3C2D4E13.70±0.104.92±0.0916A4B4C1D3E23.75±0.085.08±0.21
在进行多因素方差分析前,设原假设为各因素均对xoy面信息熵、法线信息熵没有显著性影响,显著性水平为0.05,df为自由度,当P值低于显著性水平时,将会拒绝原假设。表5、表6为多因素方差的分析结果,其中扫描角度、光照强度、输送机速度以及粉尘浓度的p值均大于0.05,而煤流量p值小于0.05,表明了扫描角度、光照角度、输送机速度以及粉尘浓度对xoy面信息熵、法线信息熵没有显著性影响,而煤流量对xoy面信息熵、法线信息熵有显著性影响。
表5 xoy面信息熵的效应检验
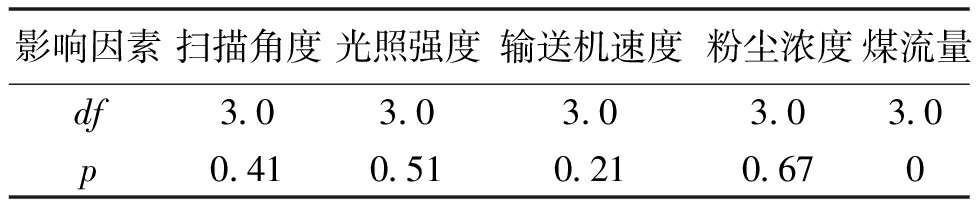
影响因素扫描角度光照强度输送机速度粉尘浓度煤流量df3.03.03.03.03.0p0.410.510.210.670
表6 法线信息熵的效应检验
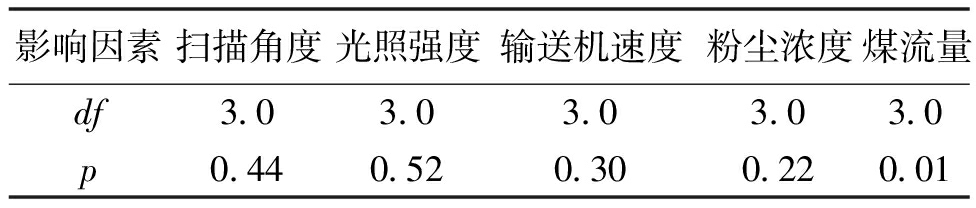
影响因素扫描角度光照强度输送机速度粉尘浓度煤流量df3.03.03.03.03.0p0.440.520.300.220.01
目前可见,煤流点云信息熵的变化主要与煤流量、噪音强度有关,点云信息熵与噪音强度呈正相关的,而与煤流量之间的变化情况尚不明确。
3.2 噪音强度预测模型
煤流点云信息熵与噪音强度呈正相关,但与煤流量之间变化情况尚不明确。为了进一步获得三者之间的关系,引入混合高斯噪声模拟矿井环境,对不同煤流量、噪音强度的点云调和信息熵进行统计,构建了煤流点云的调和信息熵等高线投影如图6所示。
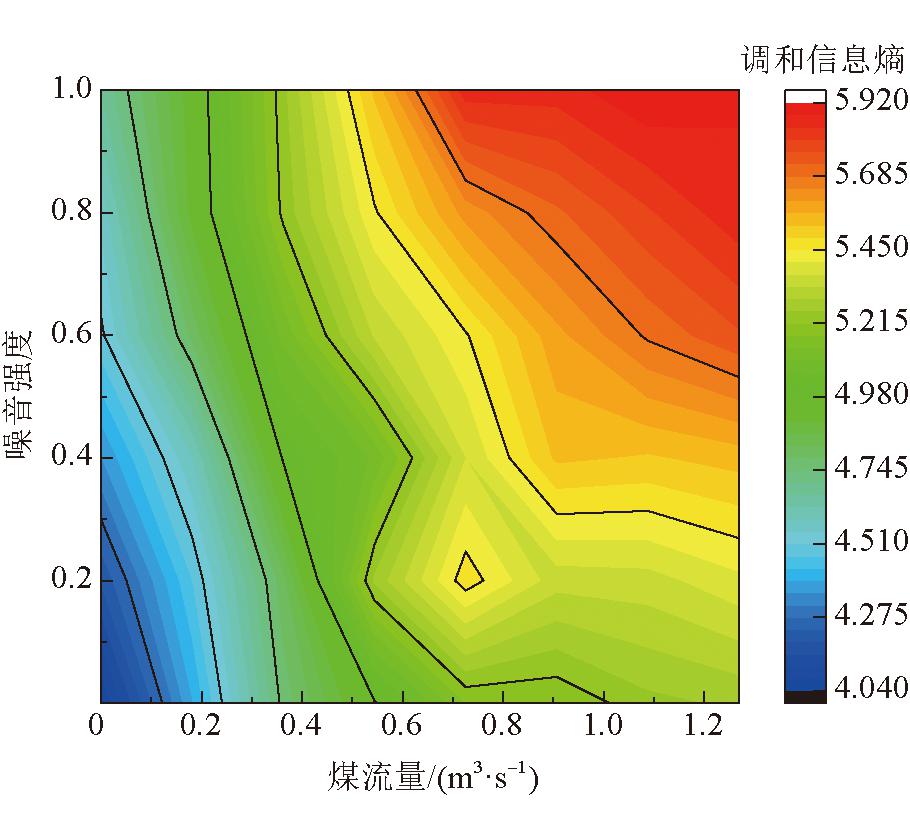
图6 调和信息熵等高线投影
式(8)为调和信息熵Hharmonic,代表xoy面信息熵与法线信息熵的调和平均数[20],反映了点云分布的整体趋势、细节变化,可同时自适应均分两种信息熵的权重。
(8)
式中:Hharmonic——调和信息熵;
![]() 测量点云xoy面信息熵;
测量点云xoy面信息熵;
H(N)——点云法线信息熵。
通过计算可得,煤流量、噪音强度与信息熵均呈现正相关,当煤流量越大、噪音越强时,信息熵越大。
根据点云信息熵变化情况,建立了一个点云噪音强度预测模型,参考了不同的曲面方程进行拟合,通过高斯-牛顿法[21]进行迭代优化。
各曲面方程的拟合情况见表7,其中R2反映了曲面的拟合效果,该值越接近1,拟合效果越好。表7中的各曲面函数光滑且参数量小,便于求解二阶导数,高斯-牛顿法不需要调整学习率,就可在有限的迭代次数逼近最优解。
表7 曲面方程拟合程度

拟合方程平面方程二次曲面多项式曲面二维高斯函数logistic函数拟合状态收敛收敛收敛不收敛收敛R20.6610.8790.883<00.334
多项式曲面拟合效果最佳,但其参数过多不易于表达,选用了拟合效果相近的二次曲面作为噪音强度![]() 的预测模型。噪音强度
的预测模型。噪音强度![]() 预测方程见式(9):
预测方程见式(9):
(9)
式中:![]() 预测噪音强度;
预测噪音强度;
A1,A2,A3,A4,A5,A0——待预测参数;
x——调和信息熵;
y——煤流量。
二次曲面参数计算见式(10):
(10)
式中:ω——二次曲面方程参数。
迭代优化的残差函数计算见式(11):
(11)
式中:L——残差函数;
![]() 第i个样本的噪音强度;
第i个样本的噪音强度;
xi——第i个样本的调和信息熵;
yi——第i个样本的煤流量。
高斯牛顿迭代的参数计算见式(12):
ωk+1≈ωk-(∇LT∇L)-1∇L
(12)
式中:ωk+1——第k+1次曲面方程参数;
ωk——第k次曲面方程参数;
▽L——残差函数L的梯度,也可视为雅可比矩阵。
曲面方程初始参数见式(13):
ω0~N(0,1)
(13)
式中:ω0——曲面方程初始参数;
N(0,1)——标准高斯分布。
噪音强度预测模型如图7所示,经高斯牛顿法的有限次迭代后,二次曲面噪音预测方程已收敛,A1、A2、A3、A4、A5、A0参数分别为1.49、0.05、-2.61、1.50、-0.16、-6.11。噪音预测模型表征了噪音强度、调和信息熵与煤流量之间的变化关系,通过调和信息熵与煤流量可以预测出煤流点云模型的噪音强度。需要注意的是,当预测的噪音强度小于0时,表明点云存在过度平滑的失真现象;预测的噪音强度大于0,表明点云数据中混有环境噪声。
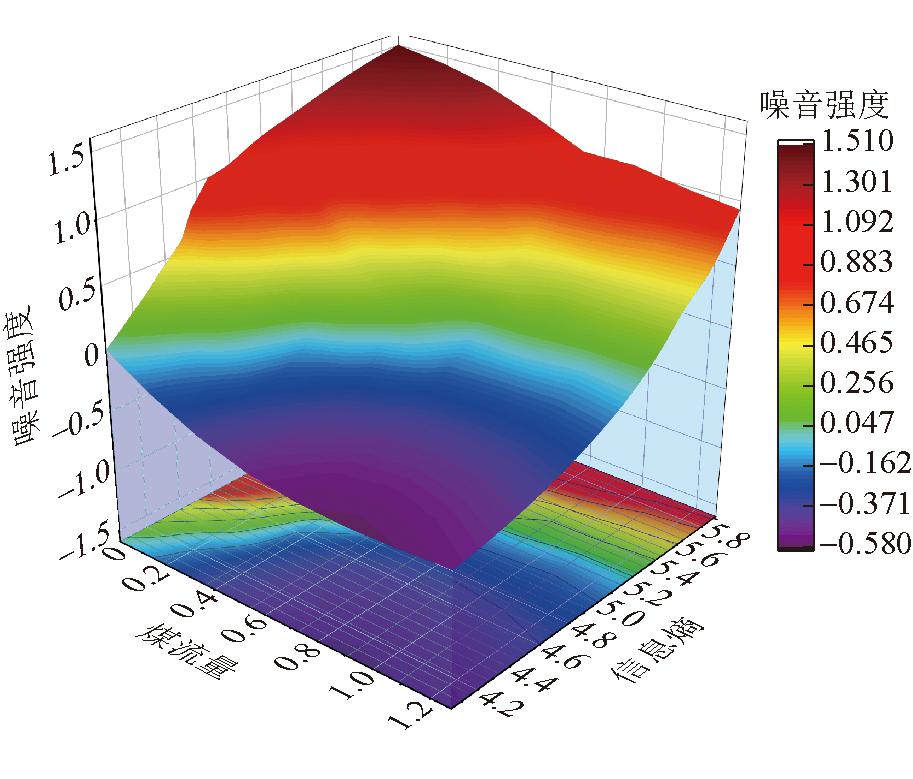
图7 噪音强度预测模型
3.3 基于噪音强度和模糊理论的点云滤波
构建噪音强度预测模型的根本目的是建立煤流点云质量优化滤波的可靠指标,利用噪音强度等反推出合适的点云滤波参数,进而得到高保真、高可靠以及高精度的煤流点云模型。
然而,噪音强度和点云滤波之间的关系,是非线性、难量化且不确定的。以高斯点云滤波为例,高斯滤波[22]的方差(sigma)参数是根据同分布的先验假设和中心极限定理确定的,而噪音强度是基于多因素方差分析和曲面方程预测出的,理论依据的差异导致两者之间的关系难以论证。由此可见,通过建立噪音强度、高斯滤波间的理论模型,进一步推理出滤波参数是明显不可行的。
尽管噪音强度、点云滤波间的理论模型是不明确的,但原则上,预测出的噪音强度越大,就需要更大的sigma参数进行平滑。为了防止分歧,噪音强度相同但分布不同的煤流点云,需要使用参数相同的高斯滤波。因此,对于所有的煤流点云,噪音强度和sigma参数应该是满映射的单一对应关系。
按照模糊数学基本理论[23],可以进行大量的模糊统计试验,建立噪音强度、sigma的隶属度函数,结合单一对应关系构建规则,量化推理噪音强度、点云滤波间的模糊关系R,最终计算噪音强度的模糊向量与模糊关系矩阵的内积,输出sigma参数的推理向量。构建和推理模糊关系图8所示。
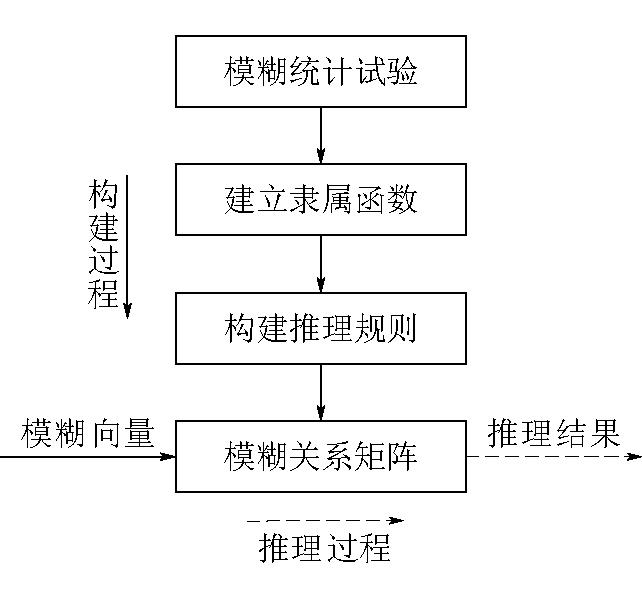
图8 构建和推理模糊关系
推理向量计算见式(14):
u=a∘R
(14)
式中:u——推理向量;
a——噪音强度的模糊向量;
R——模糊关系矩阵。
模糊统计试验主要是统计噪音强度关于高斯滤波sigma参数的成功试验频率,该试验需要至少一位专家参与。根据成功试验频率,建立噪音强度σn对S的隶属度μs(σn),其中S为代表sigma参数的模糊集合,可分为S1、S2、S3这3个模糊子集。
成功试验是指当煤流点云噪音强度为σn时,点云经sigma参数为Si的高斯滤波处理后,专家认为滤波效果可接受,计入次数;反之,则为失败试验,不计入。Nσn,Si指噪音强度为σn、sigma参数为Si试验的总次数。
成功试验频率计算见式(15):
(15)
式中:μsi(σn)——模糊子集Si的隶属度;
Nσn,Si——试验的总次数;
Vσn,Si——成功试验次数。
在构建过程中,进行了噪音强度σn为[0,1]、点云滤波sigma参数为{1,3,5}的模糊统计试验。该试验旨在统计成功试验频率,构建模糊子集隶属度μsi(σn),其中S1、S2、S3的sigma参数分别为1、3、5。可以看出,S1参数的滤波可以很好地处理噪音强度较低的点云,但是无法适应噪音强度较高的点云。而S2、S3能有效应对噪音强度较高、高的点云,却不能解决噪音强度较低的点云,侧面证明了噪音强度和sigma参数应该是单一对应的关系。隶属函数如图9所示。
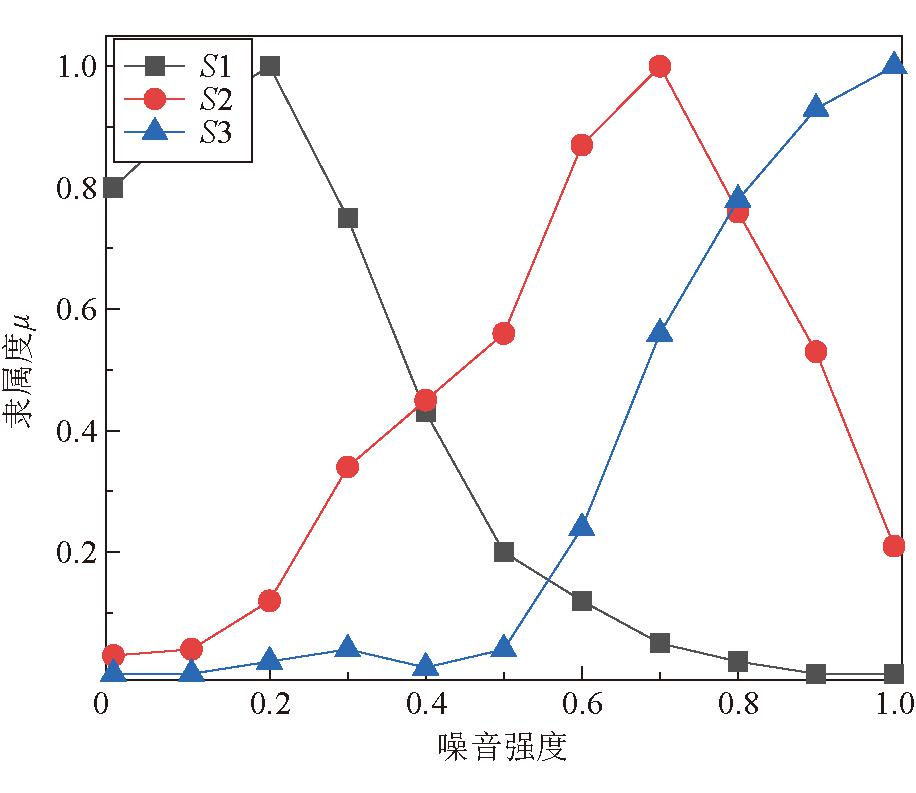
图9 隶属函数
对模糊子集隶属度函数离散化处理,拼接后构建模糊矩阵S见式(16):
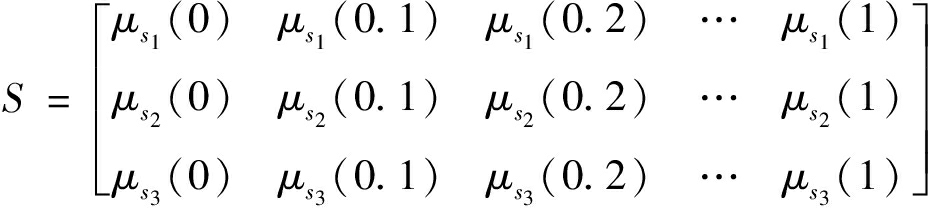
(16)
式中:μsi——模糊子集隶属度。
按照单一对应关系,给出推理规则:如果原始点云的噪音强度隶属于Si,就应当使用参数为Si的高斯滤波,其中i=1,2,3。因此,得到推理矩阵F见式(17):
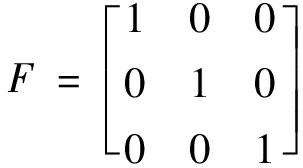
(17)
更进一步,计算模糊矩阵S的转置与推理矩阵F内积,得到模糊关系矩阵R见式(18):
R=ST∘F=ST
(18)
式中:R——模糊关系矩阵;
F——推理矩阵;
ST——模糊矩阵。
模糊数学中的内积是先交运算再并运算,本质上就是寻找共性,再放大共性的过程。由于推理矩阵F为单位矩阵,利用内积求取关系矩阵R,将不会损失信息。
在推理过程中,将输入的噪音强度σn离散化为模糊向量a,其中a=(a0,a1,a2,…a10),见式(19):
(19)
式中:ai——模糊向量中第i个分量;
σn——噪音强度。
按式(14)求取模糊向量a与模糊关系矩阵R的内积,得到推理向量u,其中u=(u1,u2,u 3),最终按平均值法,输出高斯滤波参数sigma,见式(20):
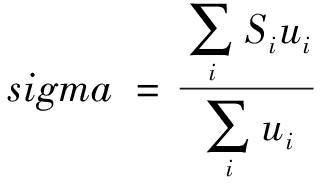
(20)
式中:sigma——高斯滤波参数;
ui——推理向量中第i个分量。
4 实验与分析
为了验证噪音预测模型的效果优劣,开展了煤矿井下激光扫描数据的实验研究。在晋能控股集团塔山煤矿8222综放工作面实地采集了大量的刮板输送机煤流点云样本。点云集中共有205组样本。实验人员对测试集中点云的噪音强度进行主观评价,组成带有噪音主观分数的测试集,见表8。
表8 噪音主观分数

序号模型品质主观噪音分数1无法观看模型0.92点云模型存在剧烈噪音,妨碍观看0.73点云模型存在一定噪音,对观看稍有妨碍0.54点云模型存在较小噪音,但不妨碍观看0.35点云模型清晰0.1
由表8可以看出,点云的模型品质分为5个档次,由人工划定点云的模型噪音强度,并给出合理的主观分数,主观分数σ的取值范围为(0,1),用于表征点云模型的噪音强度。测试集点云评分效果如图10所示。

图10 测试集点云评分效果
为测试集的稠密煤流点云,由实验人员根据表8的评分标准进行打分,其中黑色点云为煤流,绿色点云为刮板机底部背景。
以峰值信噪比(PSNR)及局部结构相似性(Mean Structural SIMilarity,MSSIM)为对照组,本文模型为实验组,均对测试集点云噪音进行打分,选取了皮尔逊相关系数(PLCC)、斯皮尔曼相关系数(SROCC)、均方误差(MSE)作为量化指标[24-25],对比算法与其他算法之间性能差距,确定算法的模型评价效果。其中皮尔逊相关系数(PLCC)、斯皮尔曼相关系数(SROCC)、均方误差(MSE)能够准确描述主观分数、客观分数之间的相关程度,反映评价模型的准确性、单调性以及一致性,可以作为衡量本文评价模型的量化指标。
在实验之前,将测试集点云均分为4个小组,1组用作评价模型性能,其余3组用于回归,重复4次作交叉验证,使每组样本都参与评价[26]。按照噪音强度预测模型原理,实验组以噪音强度(噪音分数)为因变量,煤流量、调和信息熵为自变量,进行二次曲面拟合。对照组则直接进行线性回归,将指标h(PSNR、MSSIM)线性映射到主观分数σ,wT、b为线性回归模型的参数,线性回归使用的损失函数为均方误差,见式(21):
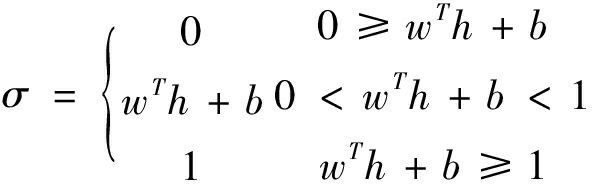
(21)
式中:σ——主观分数;
h——图像质量指标;
wT、b——线性回归模型参数;
对照实验结果如图11所示。
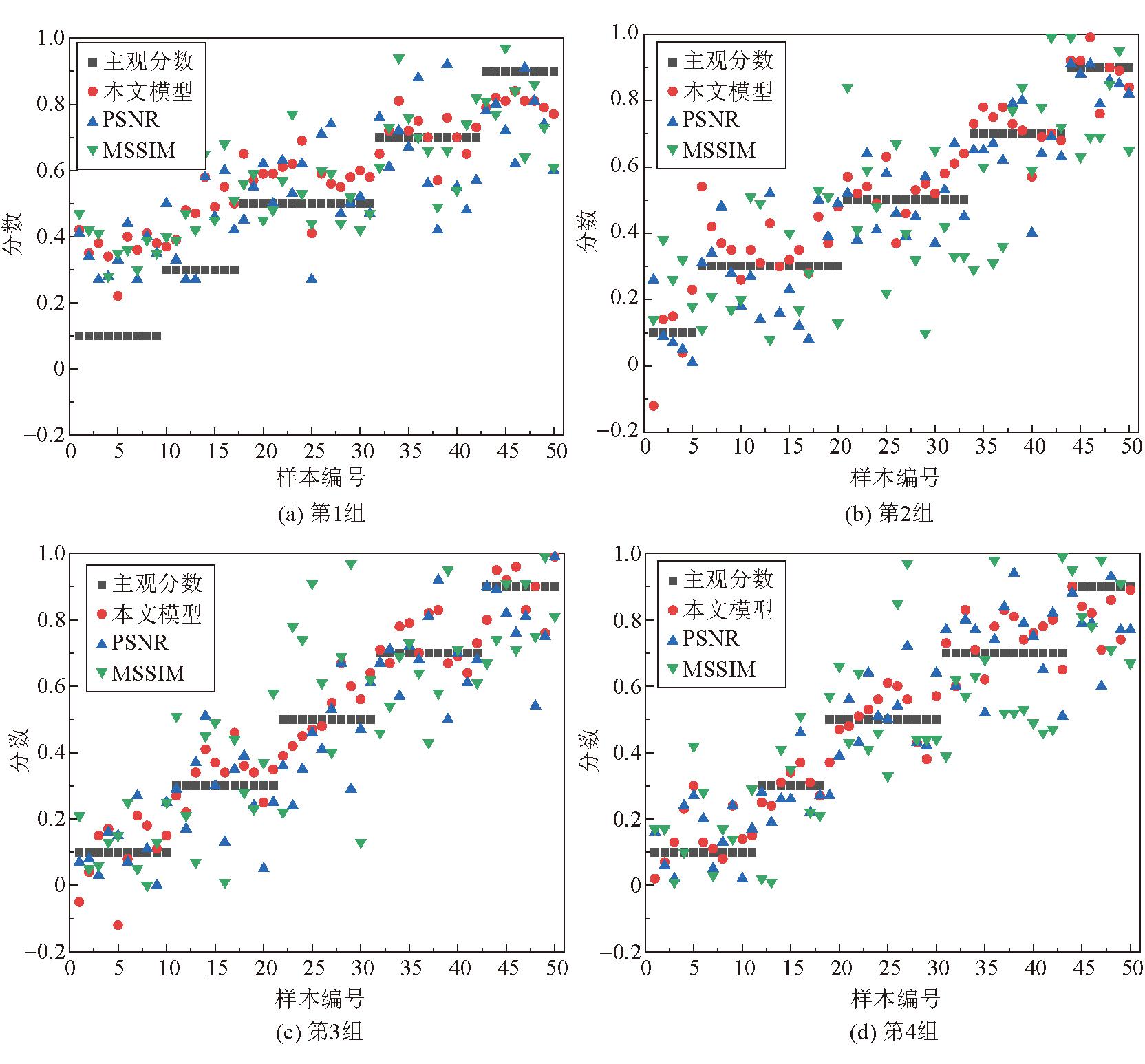
图11 对照实验结果
由图11可以看出,模型得到的分数越贴近主观分数,表明模型的量化能力越强,越能够准确描述出图像的失真程度。模型性能对比见表9。
表9 模型性能对比
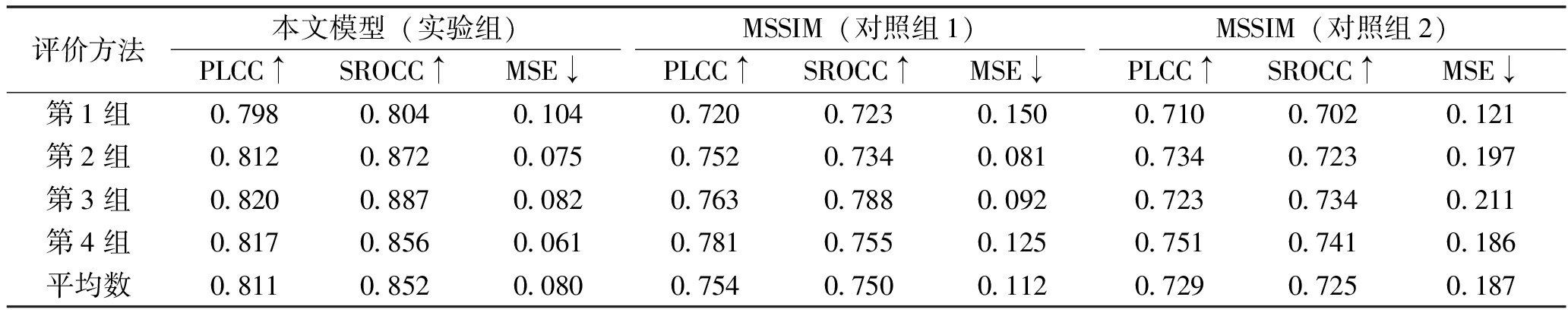
评价方法本文模型(实验组)PLCC↑SROCC↑MSE↓MSSIM(对照组1)PLCC↑SROCC↑MSE↓MSSIM(对照组2)PLCC↑SROCC↑MSE↓第1组0.7980.8040.1040.7200.7230.1500.7100.7020.121第2组0.8120.8720.0750.7520.7340.0810.7340.7230.197第3组0.8200.8870.0820.7630.7880.0920.7230.7340.211第4组0.8170.8560.0610.7810.7550.1250.7510.7410.186平均数0.8110.8520.0800.7540.7500.1120.7290.7250.187
其中PLCC、SROCC描述了模型分数与主观分数的相关程度,该值越高越好,MSE反映了模型分数与主观分数的直接差距,该值越低越好。实验组的PLCC、SROCC均值为0.811、0.852,高于PSNR、MSSIM等对照组,表明实验组算法具有比PSNR、MSSIM更好的一致性、单调性;实验组算法的MSE均值为0.080,低于对照组算法,说明实验组算法与结果有较小的偏差,比PSNR、MSSIM更加准确。
另一方面,需要探究基于噪音强度和模糊理论的点云滤波的降噪效果,验证利用噪音预测模型优化点云的可行性。噪音强度对比、PSNR对比如图12和图13所示。
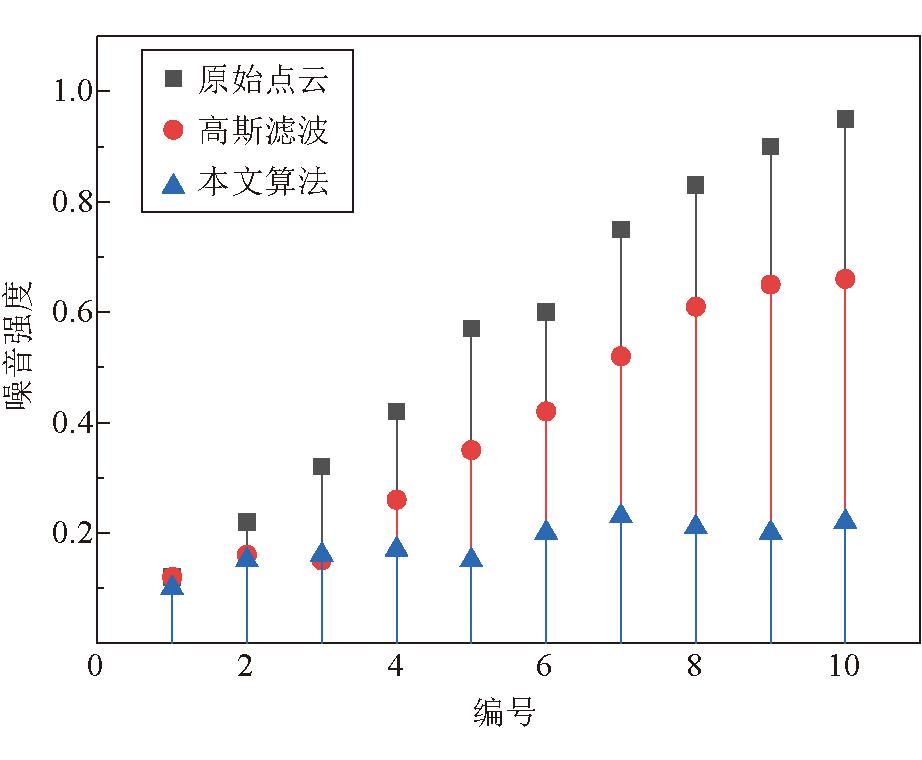
图12 噪音强度对比
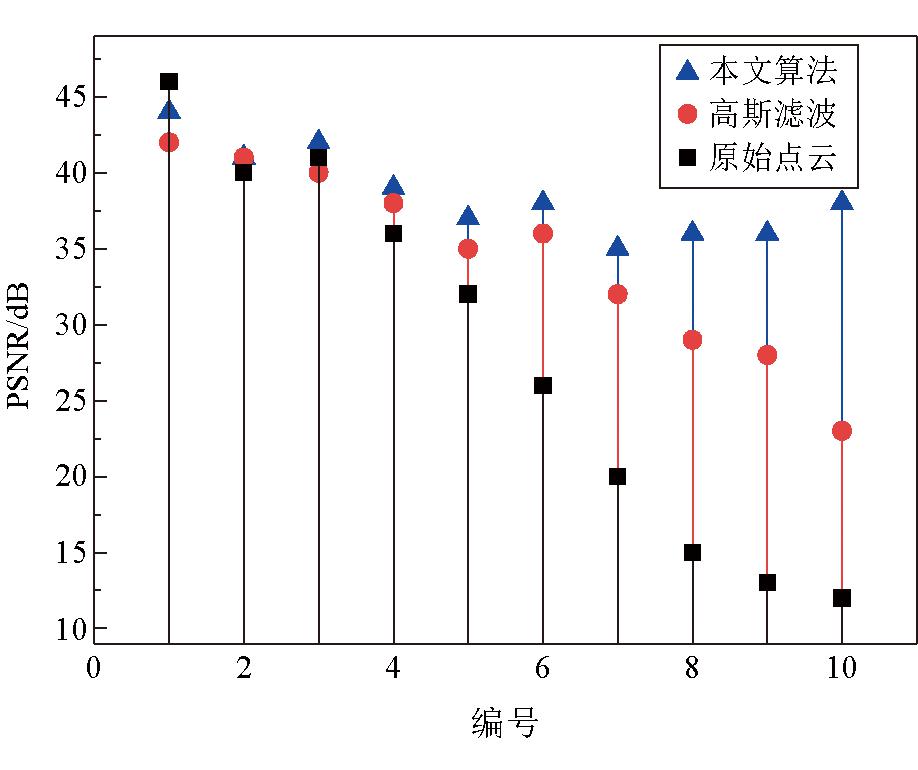
图13 PSNR对比
从点云集中随机选出10种不同质量水平的煤流点云,经本文滤波、高斯滤波处理,结合噪音强度、PSNR等指标进行图像质量评价,高斯滤波的sigma参数为1。噪音强度指标越低,点云质量越好,而峰值信噪比(PSNR)越低,点云质量越差。可以看出,本文滤波算法能够有效改善原始点云质量,对比高斯滤波,更适用于不同质量的煤流点云。
5 结论
(1)通过对煤流点云信息熵进行分析,确立了信息熵与噪音强度的相关关系,实验表明煤流点云中的噪音强度越大,煤流点云几何参数的分布就越离散,信息熵也就越大,可作为建立激光扫描数字孪生煤流点云模型质量评价方法的实验依据。
(2)实验分析了扫描角度、粉尘浓度以及煤流量等因素对信息熵的影响,根据煤流量、噪音强度以及信息熵间的关系,建立了点云模型的噪音强度二次曲面预测模型,利用高斯牛顿迭代法进行拟合优化,通过构建模糊关系矩阵,实现对点云滤波参数的模糊推理,进而得到高保真、高可靠以及高精度的煤流点云模型。
(3)验证了点云质量评价算法的实际效果,以MSSIM、PSNR作为对比算法,使用综放工作面煤流点云样本作测试数据集,并探究基于噪音强度和模糊理论的点云滤波效果,实验结果表明本文提出的算法具有更好的一致性、稳定性和单调性,更适用于煤矿井下复杂工况环境。
[1] 田臣,覃杰,王强,等.煤矿智能掘进装备发展现状与关键技术探讨[J].中国煤炭,2023,49(7):102-108.
[2] 张帆,葛世荣,李闯.智慧矿山数字孪生技术研究综述[J].煤炭科学技术,2020,48(7):168-176.
[3] 葛世荣,张帆,王世博,等.数字孪生智采工作面技术架构研究[J].煤炭学报,2020,45(6):1925-1936.
[4] 刘飞,张乐群,潘红光,等.带式输送机煤量检测技术及其发展趋势[J].中国煤炭,2023,49(9):77-83.
[5] 胡而已.融合激光扫描与机器视觉的煤流量测量研究[J].煤炭工程,2021,53(11):146-151.
[6] 胡而已,叶兰,孙益壮,等.综放工作面放煤量激光扫描自适应监测技术研究[J].中国煤炭,2022,48(11):57-66.
[7] 方玉明,眭相杰,鄢杰斌,等.无参考图像质量评价研究进展[J].中国图象图形学报,2021,26(2):265-286.
[8] 王志明.无参考图像质量评价综述[J].自动化学报,2015,41(6):1062-1079.
[9] 张淑芳,张聪,张涛,等.通用型无参考图像质量评价算法综述[J].计算机工程与应用,2015,51(19):13-23,151.
[10] 靳鑫,蒋刚毅,陈芬,等.基于结构相似度的自适应图像质量评价[J].光电子.激光,2014,25(2):378-385.
[11] ZHOU W,BOVIK A C,SHEIKH H R,et al.Image quality assessment:from error visibility to structural similarity[J].IEEE transactions on image processing:a publication of the IEEE Signal Processing Society,2004,13(4):600-612.
[12] SAXENA S,SINGH Y,AGARWAL B,et al.Comparative analysis between different edge detection techniques on mammogram images using PSNR and MSE[J].Journal of information and optimization sciences,2022(2):43.
[13] MITTAL A,MOORTHY A K,BOVIK A C.No-reference image quality assessment in the spatial domain[J].IEEE transactions on image processing:a publication of the IEEE Signal Processing Society,2012,21(12):4695-4708.
[14] WANG T H,ZHANG L,JIA H Z.An effective general-purpose NR-IQA model using natural scene statistics (NSS) of the luminance relative order[J].Signal Processing:Image Communication,2019,71:100-109.
[15] 李庆玲,翟凯,郭鸿锐,等.一种基于NDT和ICP融合的点云配准算法[J].实验技术与管理,2022,39(11):23-28.
[16] 杨光耀,毛开江,胡而已,等.过煤量激光图像智能监测技术研究[J].中国煤炭,2021,47(10):49-55.
[17] 袁礼海,李钊,宋建社.利用高斯混合模型实现概率密度函数逼近[J].无线电通信技术,2007(2):23-25.
[18] 虞鸿,吴哲夫,刘恺,等.一种从物体表面法线估计高度信息的算法[J].计算机科学,2013,40(5):311-314.
[19] 戴孟莲,周凡炜,许建开.SPSS在化学试验双因素方差分析中的应用[J].中国科技信息,2017(17):80-82.
[20] 宋辉武,刘博.例析“比值定义法”背景下的调和平均数在物理学中的应用[J].物理教学,2018,40(11):12-15.
[21] 赵淑波,李立伟.关于高斯牛顿法的注记[J].哈尔滨师范大学自然科学学报,2016,32(3):6-10.
[22] ZHAN Q,LIANG Y,CAI Y,et al.Pattern detection in airborne LiDAR data using Laplacian of Gaussian filter[J].Geo-spatial Information Science,2011,14(3):6.
[23] 张博侃.模糊数学[M].北京:北京大学出版社,2021.
[24] 王洪姣.图像质量评价方法的研究及实现[D].西安:西安电子科技大学,2014.
[25] 洪新鸽.全参考图像质量评价算法研究[D].西安:西安电子科技大学,2014.
[26] SHAN G.Monte Carlo cross-validation for a study with binary outcome and limited sample size[J].BMC Medical Informatics and Decision Making,2022,22(1):1-15.
Research on the quality evaluation method for digital twin laser scanning of mine coal flow

移动扫码阅读
LI Xiaoya,LI Menggang,HU Eryi,et al.Research on the quality evaluation method for digital twin laser scanning of mine coal flow[J].China Coal,2024,50(2):57-69.DOI:10.19880/j.cnki.ccm.2024.02.008
- 相关推荐
