巷道围岩破坏理论的模糊聚类分析研究
时间:2023-07-27 来源:中国煤炭杂志官网 分享:★ 煤矿安全 ★
巷道围岩破坏理论的模糊聚类分析研究
0 引言
在煤炭资源回采过程中,开掘巷道是不可逾越和无法避免的一道工序,巷道围岩稳定成为制约煤矿安全高效生产的一道壁垒。巷道围岩机理研究是围岩控制的基础,随弹性、塑性和流变理论[1]等基础理论在巷道围岩机理研究方面的应用,巷道围岩破坏机理呈现出多样化的趋势。在中国知网查询关键词“巷道围岩机理”相关搜索结果如图1所示,可知最近5年内,巷道围岩机理的研究学术关注度非常高。
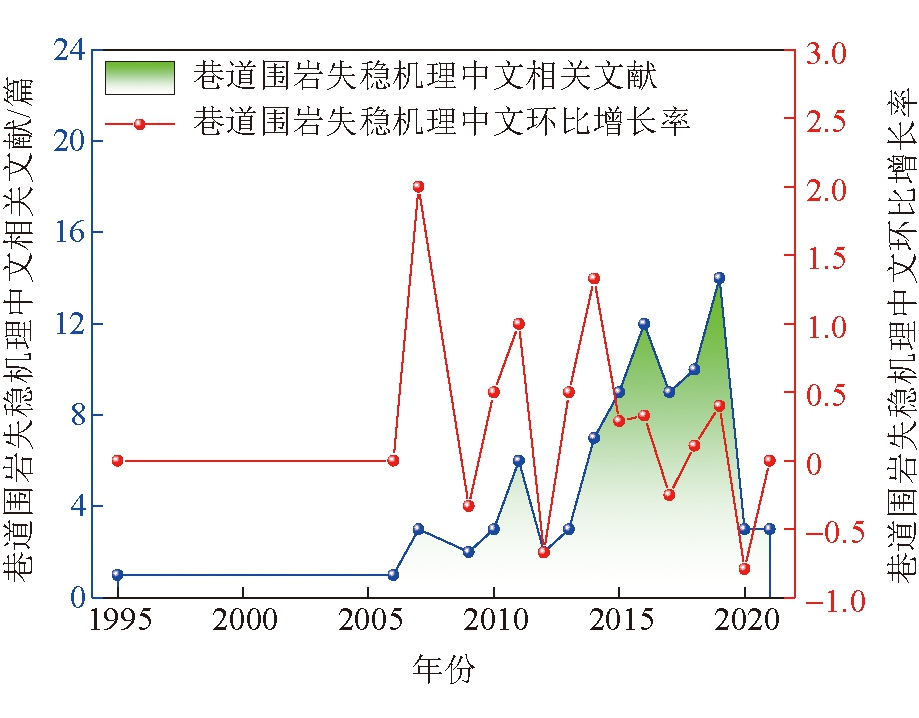
图1 巷道围岩破坏机理学术关注度
在搜索过程中,与“机理”研究高度相关的5个关键词中,“机理”研究占比最高,如图2所示。在学术界已经形成共识,只有将巷道围岩破坏的机理研究透彻,才能在巷道围岩治理方面有所突破,但是巷道所处的围岩环境变化较大,褶皱、断层、陷落柱等地质构造会加剧围岩应力环境的不确定性,也造成了巷道围岩破坏机理研究的多样性和复杂性。
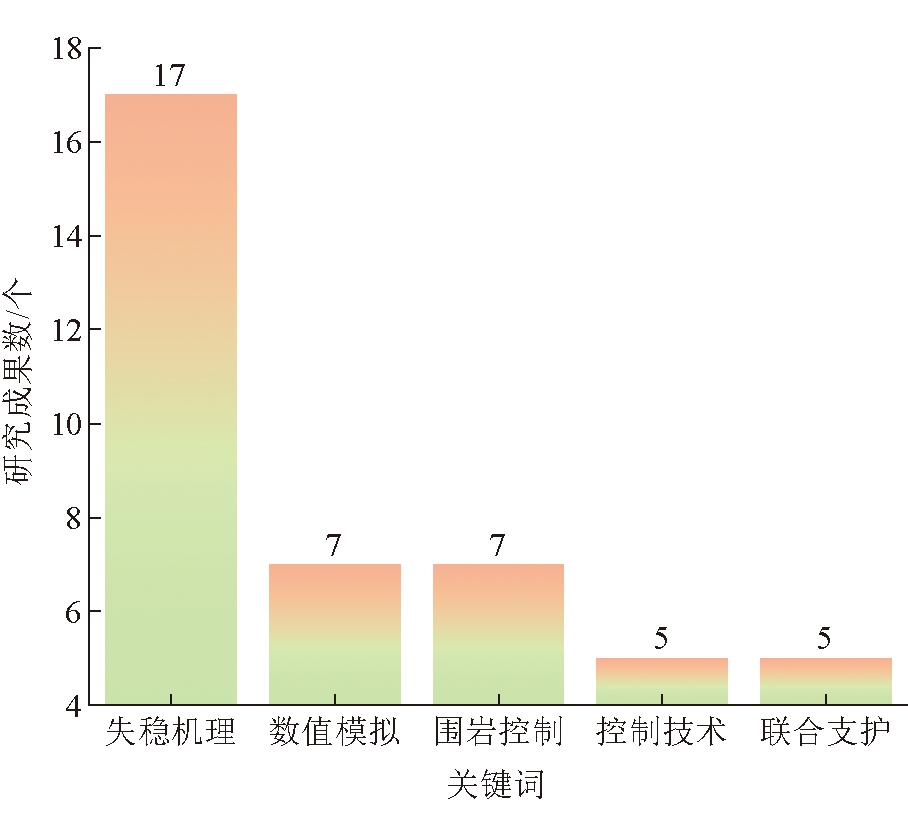
图2 巷道围岩破坏机理相关关键词
在对巷道围岩破坏情况的认识过程中,逐渐形成了4种基本理论:普式理论、轴变理论、塑性形变理论和蝶形破坏理论。但是在实际应用过程中,如何选取适应现场地质条件的巷道围岩破坏理论成为难点,笔者借助巷道破坏高度指标以模糊聚类分析方法对4种典型巷道破坏理论进行分类,经工程验证,与现场一致性较好。
1 巷道围岩破坏理论
1.1 普式冒落拱理论
以泰沙基[2](TERZAGHI)和普罗托齐雅科诺夫[3](М.М.Протодьяконов)为代表的研究人员经过长期观测发现,深埋巷道开挖后,由于节理切割,巷道顶部会产生塌落,当塌落发展到一定程度后,会自然形成一个拱形结构,支护结构所承受的压力不是上覆岩层的全部重量,只是自然平衡拱内岩体的自重,这就是最为常用的普式冒落拱理论,其计算如图3所示。
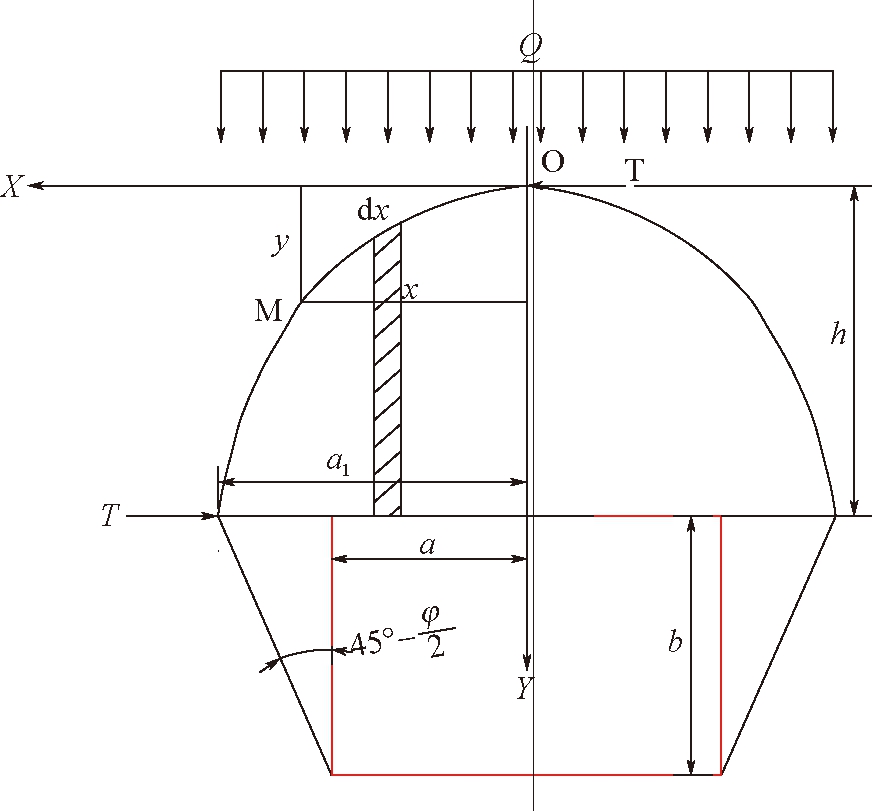
图3 普式理论巷道围岩压力计算
普式冒落拱理论假设:
(1)岩体受节理面切割,巷道围岩形成松散岩体,但仍有一定粘结性;
(2)巷道围岩顶部承受的压力仅为自然平衡拱内岩体自重;
(3)巷道侧壁产生的破裂面与侧壁的夹角为(45°-φ/2),并在巷道顶板水平面与自然平衡拱相交,形成可能塌落的扇形最大岩体;
(4)巷道顶板岩体只能承受压应力不能承受拉应力。
巷道顶板所承受的最大围岩压力[4]:
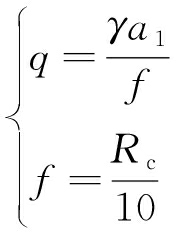
(1)
式中:q——顶板所承受的最大围压,kN;
a1——冒落拱最大可能半跨,m;
Rc——巷道围岩的单轴抗压强度,MPa;
f——岩体的坚固性系数,kN/m3;
γ——岩层的容重。
普式自然冒落拱的高度:
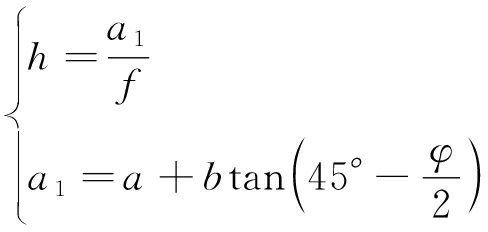
(2)
式中:h——冒落拱高度,m;
a——巷道半跨,m;
b——巷道高度,m;
φ——岩层内摩擦角,(°)。
普式理论公式简单,计算方便,在20世纪50-60年代我国隧道建设中常用[5],但在应用该理论分析围岩受力破坏过程中需要注意2个问题:巷道上部岩体厚度不大,一般巷道埋深小于2~3倍的最大平衡拱高度时,巷道不会形成平衡拱结构,因此在应用该理论分析时,巷道应具有一定的埋深;岩体的坚固性系数f为实验室岩块的计算值,在实际使用时,应根据现场施工、地下水渗漏、岩体完整性等,修正该值以全面反映岩体的力学性能。
1.2 轴变理论
20世纪50年代末,于学馥教授[6-7]研究巷道顶板冒落拱形状的过程中提出了轴变理论,该理论认为:巷道塌落又自行稳定可以用弹性理论进行分析,围岩的破坏是由于应力超过了岩体强度极限引起的,塌落改变巷道轴比,导致应力重新分布。应力重新分布的特点是高应力下降、低应力上升,并向无拉应力和均匀分布发展,直到围岩稳定而停止。围岩保持稳定的最佳自然平衡拱的形态是具有一定轴比的椭圆。
轴变理论的基本假设:
(1)在垂直均布载荷q=γH(H为巷道距地表埋深)及水平均布载荷λq作用下的压力曲线为椭圆形冒落拱的形状;
(2)椭圆平衡拱拱脚的移动决定了拱的破坏形态。
椭圆平衡拱拱脚处的水平切力:
(3)
式中:F——椭圆平衡拱拱脚处的水平切力,kN;
K——椭圆自然平衡拱拱脚处稳定状态的安全系数,K≥1;
f——顶板岩石坚固性系数,取1.5~2.0;
λ——围岩侧压力系数,当埋深小于500 m时,λ=0.5~3.5,松散软弱地层中,λ=0.5~1.0。
轴变理论椭圆形冒落平衡拱计算模型如图4所示。
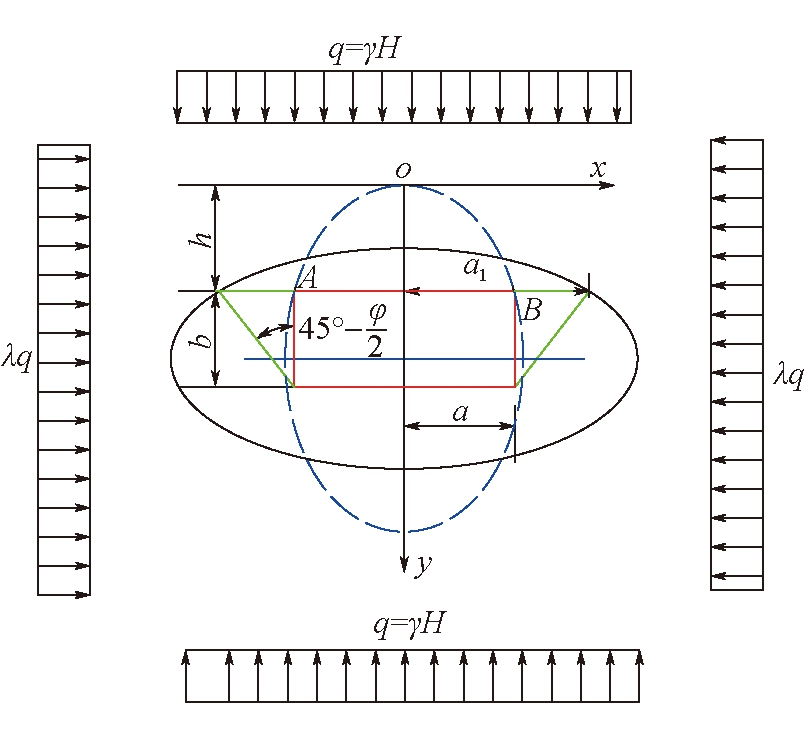
图4 轴变理论椭圆形冒落平衡拱计算模型
轴变理论冒落拱内每延米巷道顶板重量Q为:
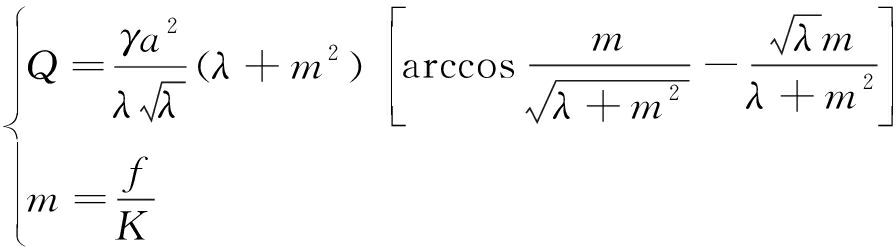
(4)
轴变理论自然冒落平衡拱的高度:
(5)
当式(5)符号为“-”时,椭圆的长轴方向水平,当符合为“+”时,椭圆的长轴方向垂直。将式(5)用泰勒级数展开,略去高阶项,当K=2,λ→0时,公式计算结果为普式冒落拱的计算公式。在实际应用过程中,轴变理论对于受结构面控制的弹性体围岩的破坏规律指导意义不明显。
1.3 塑性形变理论
塑性形变压力[8-9]是指巷道开挖后,巷道围岩应力状态重新分配,破碎岩体给支护体造成形变压力,其应力水平超过围岩自身的强度,围岩进入塑性状态,产生塑性形变,支护结构阻止围岩塑性变形产生作用在支护结构上的力,压力计算如图5所示。
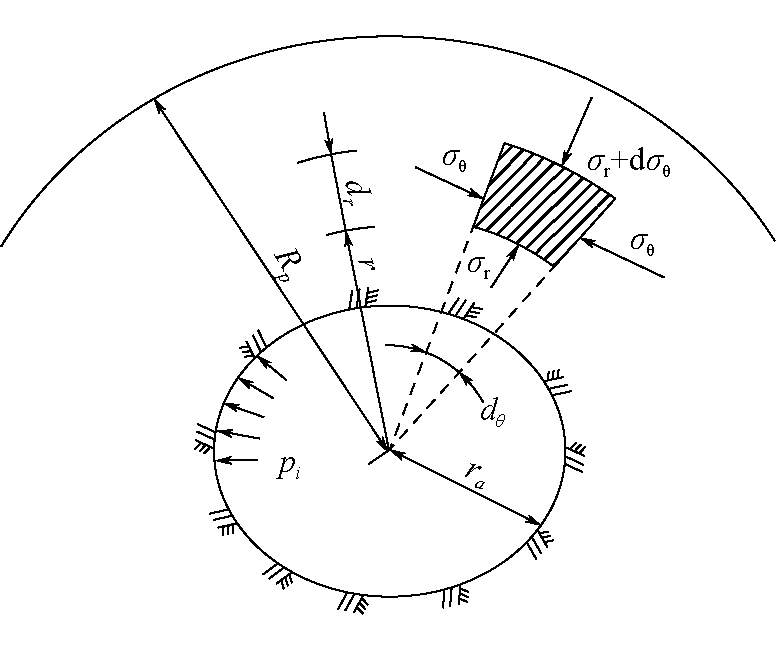
图5 塑性区形变压力计算
以芬纳(FENNER)和卡斯特奈尔(KASTNER)[10]为代表的研究人员,计算巷道围岩形变压力时,假设如下:
(1)巷道为圆形巷道,侧压力系数λ=1;
(2)弹塑性边界上,巷道围岩粘结力为零,即
r=Rp,C=0(r表示图5中以圆形巷道为圆心的半径);
(3)巷道表面围岩有支护结构,支护结构对围岩的作用力为pi,根据力的相互作用原理,该力就是所求的塑形形变压力。
经过推理,巷道塑性形变压力为:
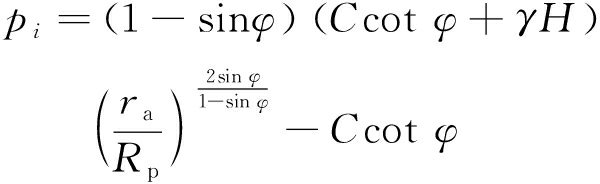
(6)
式中:Rp——巷道围岩塑性区半径,m;
pi——支护阻力,MPa;
H——巷道埋深,m;
ra——圆形巷道半径,m;
C——围岩的粘聚力,MPa;
φ——围岩的内摩擦角,(°)。
当r=Rp时,芬纳-卡斯特奈尔公式塑性区半径的表达式[11]为
(7)
从式(6)、(7)可以看出塑性区形变压力与塑性区半径呈反比,即随着塑性区半径的增大,形变压力随之减小,这是巷道卸压的原理。塑形区的大小,与已经产生的塑性变形呈正比,产生的塑性变形越大,表明岩体释放的能量越多,反之释放的能量越小。因此,塑性区半径越小,则塑性区形变压力越大。但芬纳-卡斯特奈尔公式假设塑性区边界上的粘结力为零,与实际情况有一定差别。
1.4 巷道蝶形破坏理论
马念杰教授团队以弹性力学理论为指导提出了非等压均质条件下圆形巷道围岩塑性区破坏理论,即“巷道蝶形破坏理论”[12-14],并建立了围岩蝶形破坏理论塑性区边界范围隐性方程,如方程(8)所示。
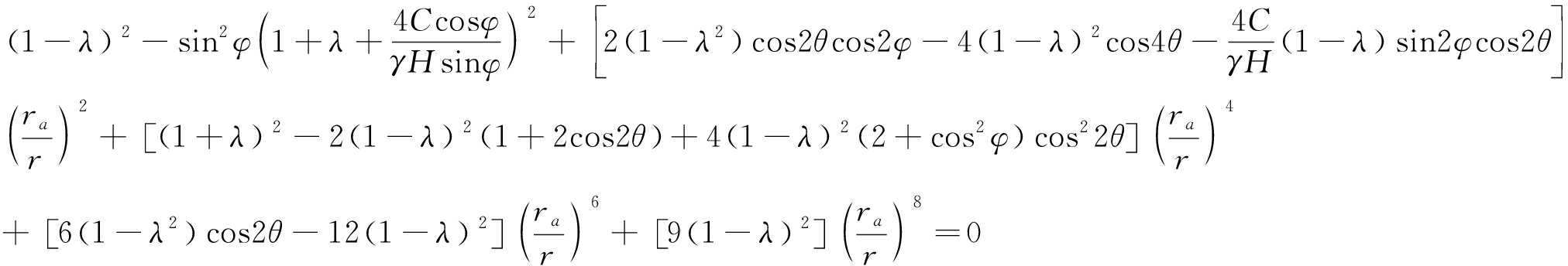
(8)
该理论认为巷道围岩破坏形态主要有圆形、椭圆形和蝶形3种形态[15],当塑性区形态在圆形和椭圆形态下,巷道围岩塑性区范围受采动及地质情况影响变化较小;当巷道塑性区呈现蝶形状态时,巷道围岩应力的细微变化都会引起巷道塑性区的急剧扩展,产生这样问题的主要原因是“蝶形”的存在,“蝶形”的存在主要是由高偏应力场引起的。不同侧压力系数下巷道围岩蝶形塑性区边界如图6所示。该理论在冒顶、片帮[16]、底鼓、深部岩层分区劣化、冲击地压[17]、煤与瓦斯突出[18-19]、地震[20]等地质力学显现方面都能给出合理的解释,并以此提出巷道围岩稳定的支护理论,进行了大量的现场试验和测试,取得了较丰富的研究成果。
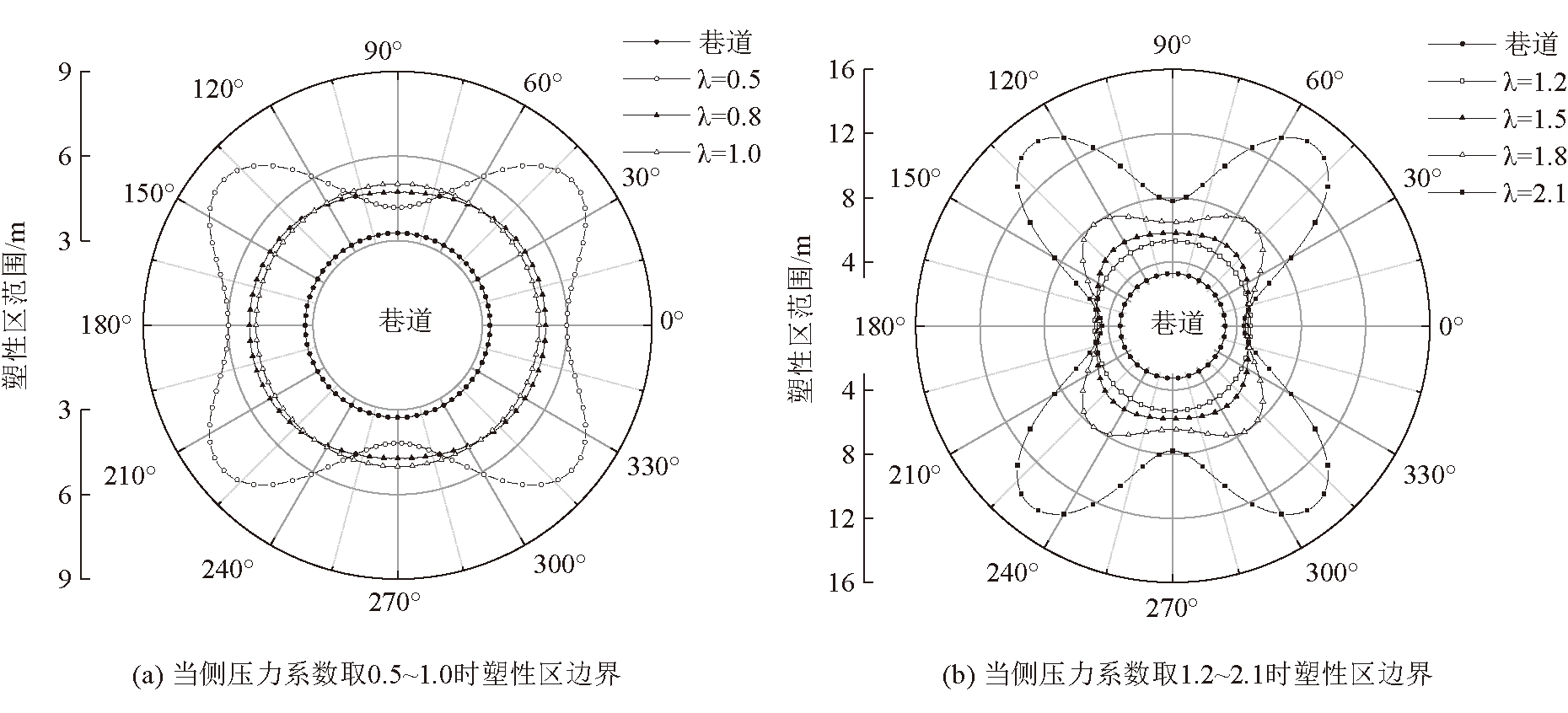
图6 不同侧压力系数下巷道围岩蝶形塑性区边界
2 巷道围岩破坏理论参数分析
各种巷道围岩破坏理论涉及的指标不尽相同,各有差异,巷道破坏理论涉及的参数越多越能细致地反映真实的围岩变形破坏情况,但是同时也提高了计算量、分析和应用难度。围岩破坏理论参数对比见表1。由表1可以看出,普式理论有3个指标,轴变理论有7个指标,塑性形变压力理论有6个指标,蝶形破坏理论有6个指标。这些指标可以分为4类:客观的应力条件(γ,H,λ)、岩石力学性质(C,φ,R)、巷道断面及支护设计(a,b,ra,pi)和冗余度(K)。
表1 围岩破坏理论参数对比
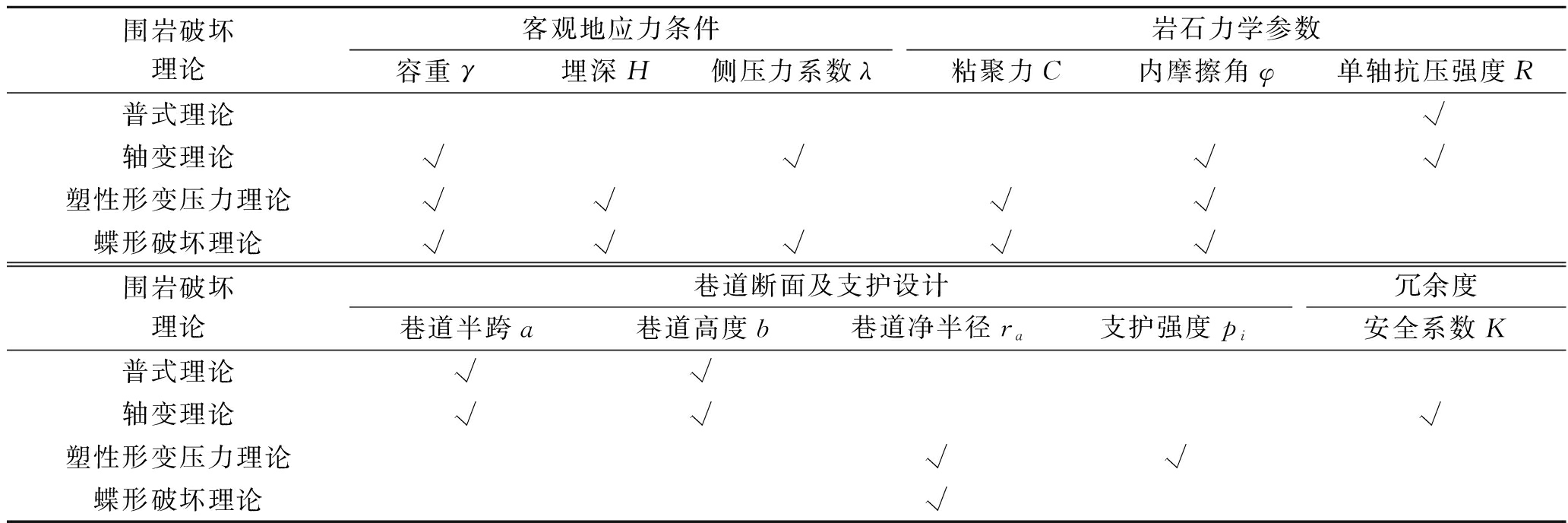
围岩破坏理论客观地应力条件容重γ埋深H侧压力系数λ岩石力学参数粘聚力C内摩擦角φ单轴抗压强度R普式理论√轴变理论√√√√塑性形变压力理论√√√√蝶形破坏理论√√√√√围岩破坏理论巷道断面及支护设计巷道半跨a巷道高度b巷道净半径ra支护强度pi冗余度安全系数K普式理论√√轴变理论√√√塑性形变压力理论√√蝶形破坏理论√
经过对比可知,各个巷道围岩破坏理论选取的指标不尽相同,在应用过程中都存在局限性,如何选择合适的计算方法进行支护设计制约着巷道支护设计的优劣。为定量研究各个巷道围岩破坏理论的优劣需要借助统计学中模糊聚类分析方法,对各个理论进行总结、归类,计算各理论巷道围岩破坏的范围,根据煤矿已有的开采经验和数据,选取合适巷道围岩破坏理论进行应用。
3 巷道破坏理论的模糊聚类分析
利用统计学中模糊聚类分析方法进行聚类分析,首先需要定量计算在特定地质条件下巷道围岩破坏范围,将其作为模糊分类的基础数据;其次将数据进行归一化处理;最后将标准化数据列成矩阵,将分析结果进行定量模糊数据计算,并根据模糊聚类分析结果进行分类。
3.1 模糊聚类分析流程
(1)用X(i)表示各个巷道围岩破坏理论计算的最大破坏深度,并将数据离差标准化处理:
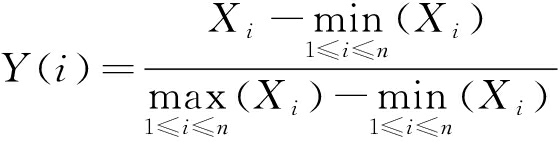
(9)
(2)计算Y(i)两两之间的距离,得到距离阵D(0)初始每个理论计算结果自成一类,此时:
Dij=(dij)n×n
(10)
式中:dij——Y(i)与Y(j)之间差值的绝对值。
(3)构建模糊矩阵:
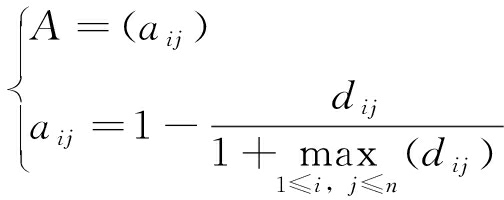
(11)
式中:aij——模糊矩阵A中的各个元素数值。
(4)将模糊矩阵A进行褶积,转化为模糊等价矩阵:
(12)
(5)聚类分析:首先将![]() 由大到小排列,依次取
由大到小排列,依次取![]() 求出对应k截距阵
求出对应k截距阵![]() 其中元素为1的两个样品归为一类,随着k的变小,合并的类越来越多,当
其中元素为1的两个样品归为一类,随着k的变小,合并的类越来越多,当![]() 将全部样品归为一类。
将全部样品归为一类。
(6)绘制聚类图。根据模糊聚类分析结果,绘制聚类图,分析结果。
3.2 不同岩性条件下围岩破坏理论聚类分析
客观地质条件与巷道断面设计参数相同情况下,利用模糊聚类分析方法,计算不同岩性条件下围岩破坏理论的聚类分析。不同岩石力学参数见表2。
表2 不同岩石力学参数

岩性粘聚力C/MPa内摩擦角φ/(°)单轴抗压强度R/MPa软岩1.02215中硬岩2.52520硬岩4.22656
岩体客观地质条件:容重γ=25 kN/m3,埋深H=300 m,侧压力系数λ=1.2。
巷道断面及支护设计参数条件:巷道半跨a=2.5 m,巷道高度b=3.3 m,支护强度pi=0,安全系数K=2。
根据表1中4种基本巷道围岩破坏理论的排列方式,各个理论计算的巷道围岩破坏最大深度见表3。
表3 各围岩破坏理论计算最大深度
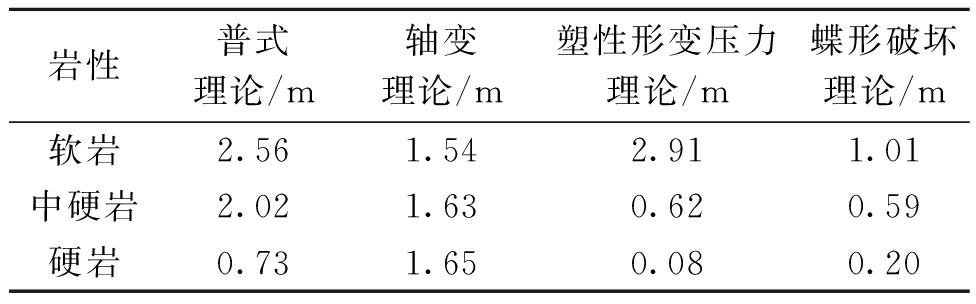
岩性普式理论/m轴变理论/m塑性形变压力理论/m蝶形破坏理论/m软岩2.561.542.911.01中硬岩2.021.630.620.59硬岩0.731.650.080.20
以中硬岩参数为代表,演示模糊聚类分析过程,以最大破坏深度为矩阵,记为X,则:
X(i)={2.02,1.63,0.62,0.59}
(13)
将以上数据做离差标准化处理,得:
Y(i)={1.000,0.727,0.021,0}
(14)
生成距离矩阵D(0):

(15)
构建模糊矩阵A:

(16)
利用褶积算法求解模糊矩阵A的模糊等价矩阵![]()

(17)
根据模糊等价矩阵![]() 的定义:
的定义:![]()
将模糊等价矩阵对应分类的数据由大到小排列为:1.000→0.727→0.021→0。
根据k值由大到小取不同数值进行分类。
(1)取k=1.000,得其k截距阵:
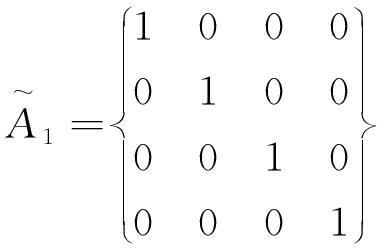
(18)
显然4个样品各成一类,即各个巷道围岩破坏理论独立成体系。
(2)取k=0.727,得其k截距阵:
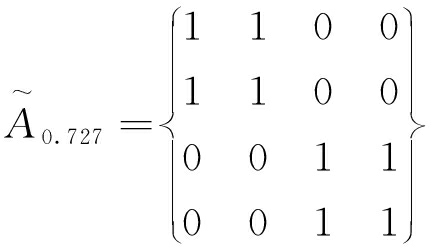
(19)
说明k=0.727时,普式理论和轴变理论归为一类,塑性形变理论和蝶形破坏理论归为一类。
(3)取k=0.021或0时,得其k截距阵:
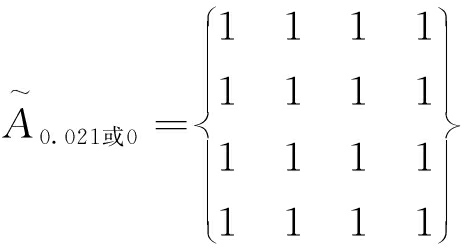
(20)
说明k=0.021或0时4种理论可以归为一类。
中硬岩、软岩、硬岩模糊聚类分析结果如图7所示。从图7可知,当巷道围岩为软岩时,普式理论与塑性形变压力理论划归一类,轴变理论与蝶形破坏理论划归一类;当巷道围岩为中硬岩时,普式理论与轴变理论划归一类,塑性形变压力理论与蝶形破坏理论划归一类;当巷道围岩为硬岩时,4种理论计算的结果相差较大,各个巷道围岩破坏理论自成体系,无法聚类。
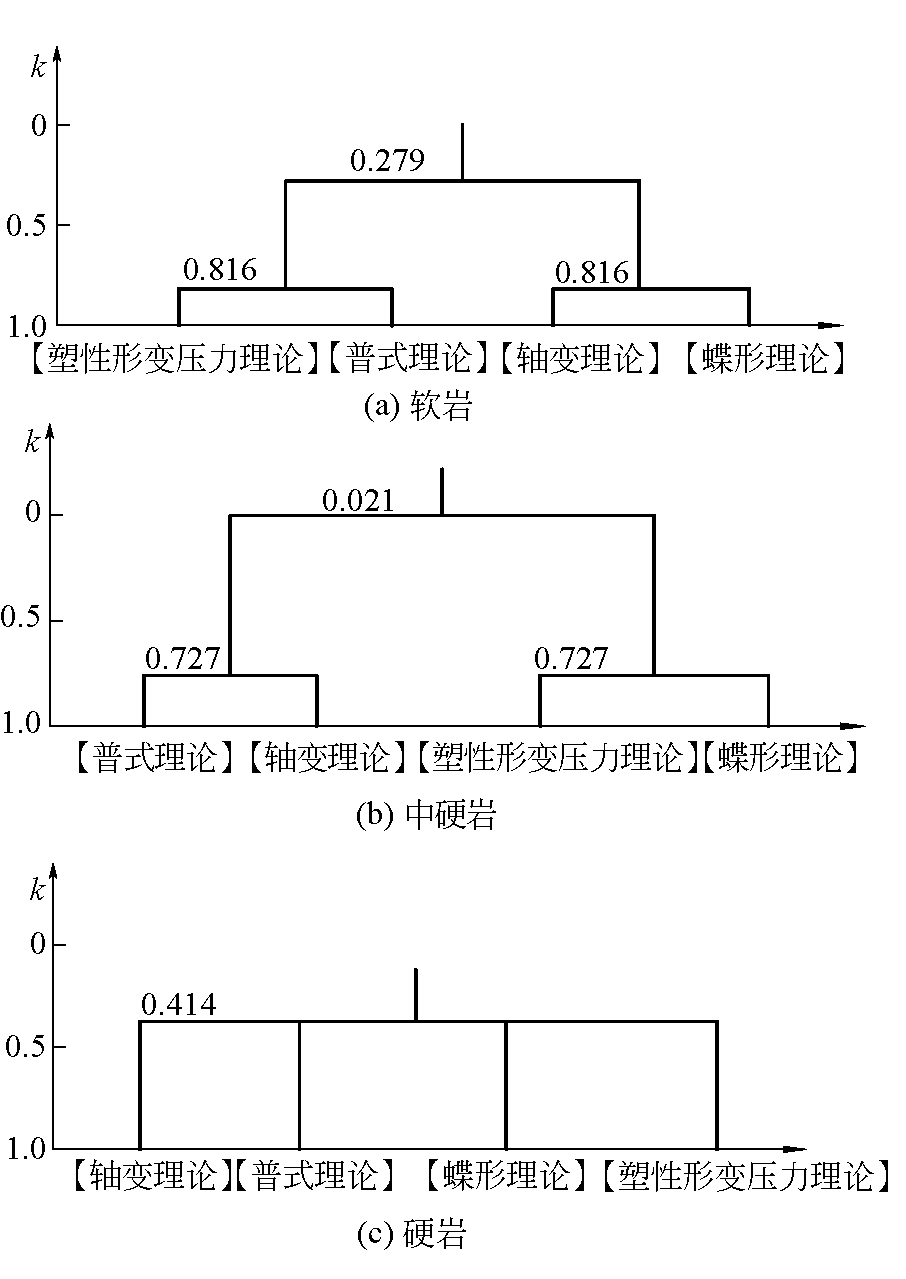
图7 软岩、中硬岩、硬岩模糊聚类分析结果
3.3 模糊聚类分析结果在支护设计中的应用
各种巷道围岩破坏理论均有其局限性,模糊聚类分析表明,针对不同岩性各个围岩破坏理论计算结果不统一,给支护设计造成巨大的困扰。因此,建议在巷道支护设计过程中,对巷道围岩进行聚类分析,找出相同类型,同类之间取加权平均值,异类之间取最大值。将最大值标记为巷道围岩破坏范围。
巷道初步支护设计时可依据巷道围岩破坏范围选取锚杆及锚索等支护材料及参数。巷道补强支护设计时,若经过计算,当巷道破坏范围在锚杆控制范围内时,采用锚杆补强;当巷道破坏范围超过锚杆长度,但未超过锚索长度时,应采用锚杆、锚索联合支护方式补强。当巷道破坏范围超过锚索支护长度时,应采用木垛、架棚等被动支护方式控制围岩,防止围岩发生冒顶事故。
4 工程应用实例
为验证模糊聚类分析支护设计方法的可行性,以五家沟煤矿巷道围岩地质条件为工程背景,验证该方法的可行性。五家沟煤矿巷道沿底板掘进,煤层平均厚度10.5 m,巷道直接顶板是7 m以上的煤层,煤层本身强度较低,抗拉、抗压和抗剪能力弱,可视为软岩。经调研,巷道冒顶统计情况如图8所示,煤巷最大冒顶高度6.0 m。
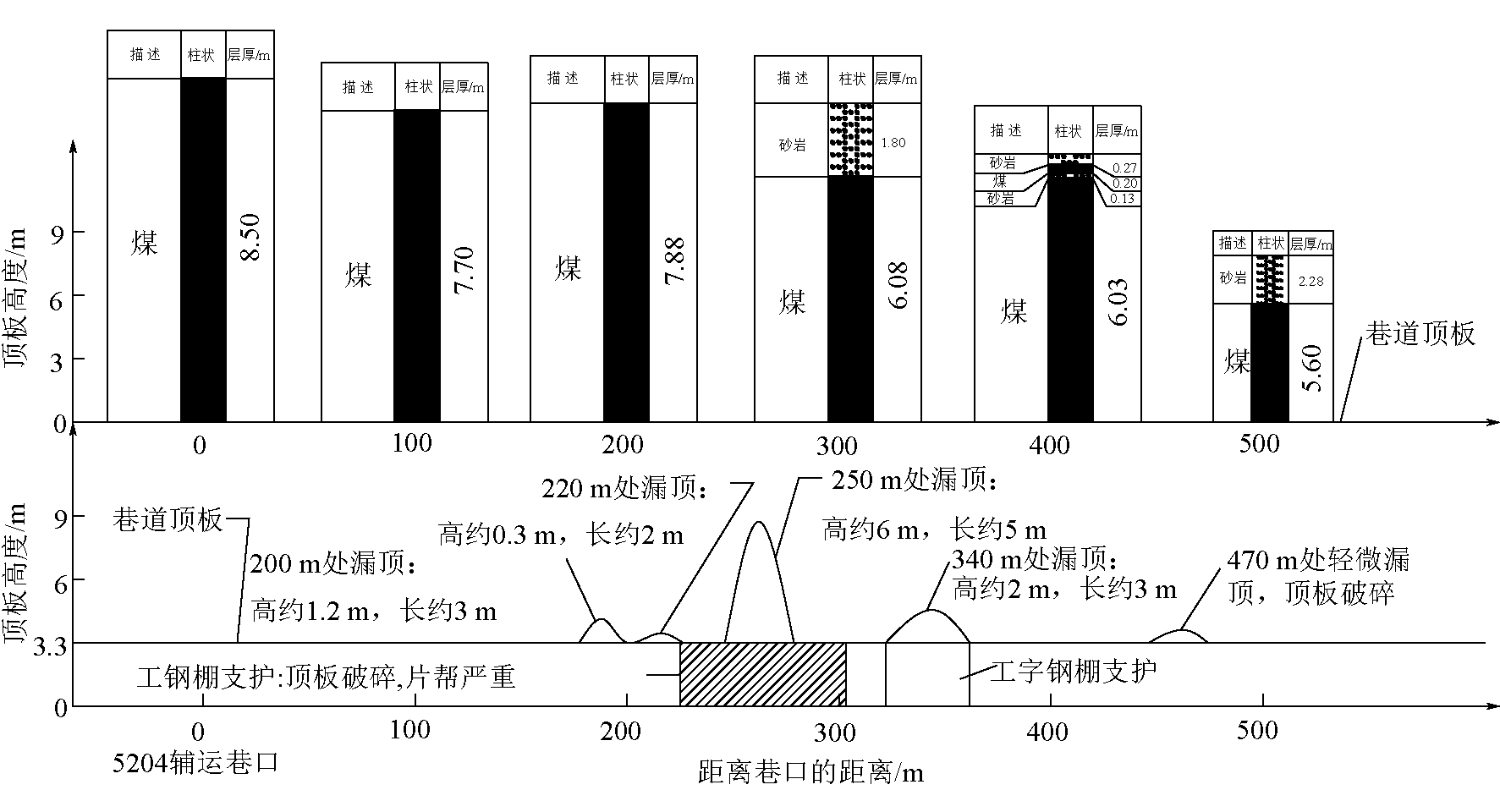
图8 巷道围岩结构及冒顶素描
(1)岩体客观地质条件:容重γ=25 kN/m3,埋深H=240 m,侧压力系数λ=1.5。
(2)岩石力学参数:粘聚力C=0.5 MPa,内摩擦角φ=23 °,单轴抗压强度R=5.93 MPa。
(3)巷道断面及支护设计参数:巷道半跨a=2.5 m,巷道高度b=3.3 m,支护强度pi=0,安全系数K=2。
经过计算,普式理论巷道破坏范围6.58 m,轴变理论巷道破坏范围1.51 m,塑性形变压力理论巷道破坏范围5.56 m,蝶形破坏理论巷道破坏范围1.42 m。
煤巷模糊聚类分析结果如图9所示,普式理论与塑性形变压力理论划归一类,轴变理论与蝶形破坏理论划归一类,与软岩分析结论一致。
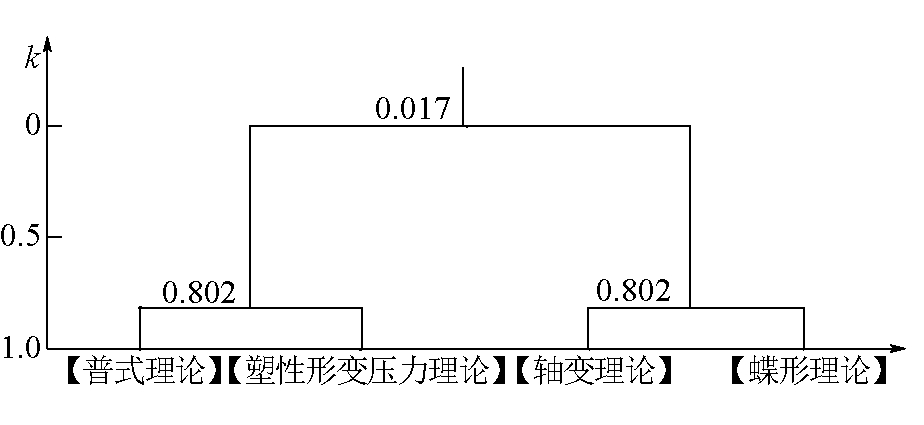
图9 煤巷模糊聚类分析结果
根据模糊聚类分析方法,计算巷道围岩破坏理论最大破坏范围:
(21)
经计算煤层巷道最大破坏深度6.07 m,与实际调研煤巷冒顶情况一致,该矿实际采用锚杆、锚索协同支护,与模糊聚类分析支护设计方法设计原则一致。因此,模糊聚类分析支护设计方法具有实际可行性。
5 结论
(1)普式理论、轴变理论、塑性形变压力理论和蝶形理论4种巷道围岩破坏理论均有其适用性,依据软岩、中硬岩、硬岩3种典型岩性的巷道围岩破坏高度聚类分析结果表明,当岩性不同时,巷道围岩破坏理论聚类分析存在差异性。
(2)以巷道围岩破坏高度为指标,借助模糊聚类分析方法将各巷道围岩破坏理论进行了分类,解决了巷道围岩破坏理论选取的难题。
(3)模糊聚类分析结果可为巷道支护设计提供参考,优化巷道支护设计过程,使得计算结果能更接近现场实际情况。
[1] 经纬,郭瑞,杨仁树,等.考虑岩石流变及应变软化的深部巷道围岩变形理论分析[J].采矿与安全工程学报,2021,38(3):538-546.
[2] 张钦喜,李继红.地基承载力的新计算方法[J].岩土工程学报,2010,32(S2):37-41.
[3] 谷拴成,史向东,王恩波.层状岩体中矩形巷道顶板破坏高度[J].煤矿安全,2014,45(12):61-63,67.
[4] GUPTA D, NATARAJAN N. Prediction of uniaxial compressive strength of rock samples using density weighted least squares twin support vector regression[J].Neural Computing and Applications,2021,33:15843-15850.
[5] YUAN Q, ZHANG Z, XIONG Q, et al.Analysis on deformation and stability of tunnel anchor excavation under broken rock mass[J].IOP Conference Series: Earth and Environmental Science,2021,783(1):1-6.
[6] 于学馥.轴变论与围岩变形破坏的基本规律[J].铀矿冶,1982(1):8-17,7.
[7] 于学馥,乔端.轴变论和围岩稳定轴比三规律[J].有色金属,1981(3):8-15.
[8] 王建宇.对形变压力的认识——隧道围岩挤压性变形问题探讨[J].现代隧道技术,2020,57(4):1-11.
[9] 任青文,张宏朝.关于芬纳公式的修正[J].河海大学学报(自然科学版),2001(6):109-111.
[10] 李永恩,郭晓菲,马念杰,等.孔洞围岩塑性区边界计算的理论研究现状与分析评价[J].煤炭科学技术,2021,49(5):141-150.
[11] 赵志强,马念杰,刘洪涛,等.巷道蝶形破坏理论及其应用前景[J].中国矿业大学学报,2018,47(5):969-978.
[12] 郭晓菲,郭林峰,马念杰,等.巷道围岩蝶形破坏理论的适用性分析[J].中国矿业大学学报,2020,49(4):646-653,660.
[13] 马念杰,郭晓菲,赵志强,等.均质圆形巷道蝶型冲击地压发生机理及其判定准则[J].煤炭学报,2016,41(11):2679-2688.
[14] 郭晓菲,马念杰,赵希栋,等.圆形巷道围岩塑性区的一般形态及其判定准则[J].煤炭学报,2016,41(8):1871-1877.
[15] 杨真,连小勇.超前支承压力对巷道顶板和两帮影响的差异化研究[J].煤炭技术,2020,39(4):33-36.
[16] 吕华新,连小勇.松动爆破技术在综采工作面压架处理中的应用[J].煤炭科学技术,2017,45(8):164-169.
[17] 马念杰,张文龙,李军,等.冲击地压机理要素分析与评价[J].矿业科学学报,2021,6(6):651-658.
[18] 张勇,连小勇,李军.煤矿瓦斯爆炸事故隐患及风险的表征方法[J].工业安全与环保,2022,48(1):42-45,59.
[19] 赵希栋. 掘进巷道蝶型煤与瓦斯突出启动的力学机理研究[D].北京:中国矿业大学(北京),2017.
[20] 马骥,赵志强,师皓宇,等.基于蝶形破坏理论的地震能量来源[J].煤炭学报,2019,44(6):1654-1665.
Study on fuzzy cluster analysis of roadway surrounding rock failure theory
LIAN Xiaoyong, LI Jun, WU Zheng, et al. Study on fuzzy cluster analysis of roadway surrounding rock fail-ure theory [J]. China Coal,2023,49(6): 37-45..DOI:10.19880/j.cnki.ccm.2023.06.006
- 相关推荐

