基于DBN的掘进工作面煤尘爆炸事故风险预测
时间:2023-03-04 来源:中国煤炭杂志官网 分享:★ 煤矿安全 ★
基于DBN的掘进工作面煤尘爆炸事故风险预测
0 引言
在煤矿掘进工作面生产施工过程中,往往会产生大量的煤尘。这些煤尘是煤矿掘进工作面作业的严重灾害源之一,具有不可忽视的潜在爆炸风险,严重威胁煤矿掘进工作面的安全生产[1]。因此,研究煤矿掘进工作面煤尘爆炸事故,寻找造成其煤尘爆炸事故的根本因素,具有重要意义。景国勋等[2]通过研究煤质指标对煤尘爆炸的影响,利用20 L球形爆炸容器对具有不同工业成分的煤尘爆炸最大压力上升速率进行测定,建立煤质指标与爆炸最大压力上升速率的计算模型;裴蓓等[3]通过对煤尘爆炸初期与瓦斯的耦合爆炸灾害强化的产生机制探究,认为初始爆炸强度对瓦斯/煤尘复合体系有重要影响;ZHANG Leilin等[4]通过建立不同弯曲角度的管道爆炸系统,研究了管道弯曲角度对煤尘爆炸传播规律的影响,认为爆炸后冲击波的峰值超压急剧增大,拐角后又缓慢减小。
目前随着人工智能技术的发展,动态贝叶斯网络(DBN)被大量运用到事故风险分析和预测方面。王文和等[5]利用DBN对城镇燃气管网进行动态分析,认为该方法克服了传统风险分析方法的不足,可动态反映燃气管网失效和事故后果发生概率随时间变化的特征。同时,DBN还可用于水下连接器故障诊断、煤矿安全态势感知[6-8]等诸多方面。
由于前人对煤尘爆炸的相关分析多集中于煤尘爆炸机理实验探究或单一因素对煤尘爆炸的影响[1-4],而对于造成煤尘爆炸事故风险分析及预测的相关研究较少,因此其分析结果具有一定局限性。DBN作为目前被广泛应用于事故风险分析和预测的手段之一,通过运用条件概率和时间序列能够很好反映造成事故的各个风险因素概率随时间变化的情况,因此笔者将通过DBN对掘进工作面煤尘爆炸事故进行分析,寻找掘进工作面煤尘爆炸事故中应重点关注的基本风险因素,为预防掘进工作面煤尘爆炸事故提供客观科学的依据。
1 事故风险分析方法
1.1 动态贝叶斯网络
DBN是静态贝叶斯网络(BN)的扩展,可以容纳时间序列数据,适用于对动态系统进行建模[9]。DBN主要由初始网络U0和状态转移网络Ut构成[10],初始网络为BN,而状态转移网络则是2个相邻时间片上网络模型。
由于掘进工作面煤尘爆炸事故的发生是一个动态过程,且掘进工作面煤尘爆炸事故具有不确定性、不完整性和时间相关性的特点,因此选用DBN作为掘进工作面煤尘爆炸事故风险分析方法。对于DBN事故分析方法,通常有以下2条假设[11]:
(1)稳定性。对于所有时间切片t,其转移概率PU(t)(Xt|Xt-1)总是相同的。
(2)马尔科夫性。对于t+1时间切片中的节点,其节点状态仅与t时间切片中节点状态有关,与t-1时间切片中节点状态无关。
对于满足上述2个条件所构建的用于掘进工作面煤尘爆炸事故分析的DBN中,任意风险因素概率分布公式为:
(1)
式中:P(Xi(t))——t时刻风险因素的概率;
P(Ut|Xi(t))——任意风险因素在转移网络中的条件概率。
DBN推理的依据与BN推理依据相同,均依据贝叶斯公式进行推理:
(2)
1.2 DBN模型要素
由于影响掘进工作面煤尘爆炸事故的风险因素有很多,在结合国家矿山安全监察局(原国家煤矿安全监察局)关于山东能源肥城矿业集团梁宝寺能源有限责任公司“8·20”煤尘爆炸事故通报[12]与前人相关分析的基础上[13],从煤尘性质、环境因素影响、管理缺陷、通风时间与通风设计不合理这4个方面对掘进工作面煤尘爆炸事故基本风险因素进行选取,共选取15个造成掘进工作面煤尘爆炸事故的基本风险因素,分别为:煤尘粒径分布X0、煤尘挥发分X1、煤尘爆炸性指数X2、煤尘水分及灰分X3、煤尘浓度在爆炸范围X4、瓦斯浓度X5、工作面风速不合理X6、氧气浓度X7、环境火源X8、通风时间不合理X9、局部通风方案设计不合理X10、整体通风方案设计不合理X11、除尘措施未落实X12、无相关安全培训X13、规章制度不健全X14,并根据事故因果关系建立初始贝叶斯网络。将掘进工作面煤尘爆炸事故作为初始贝叶斯网络叶节点,二级风险因素作为初始贝叶斯网络中间节点,15种基本风险因素作为初始贝叶斯网络根节点。
初始贝叶斯网络中的中间节点与根节点的设置状态如下:
(3)
将中间节点与根节点设置为2种状态,用于简化网络和减少中间节点数量以及优化网络计算。
将叶节点T按发生事故可能造成的后果严重程度设置状态如下:

(4)
将叶节点T按事故后果的5个等级设置为3种状态,贴近于实际情况,同时可简化计算过程,减小样本所需数据量,以实现DBN在有限信息条件下的定量推理。
1.3 基于D-S证据理论与G1法确定专家权重
在应用DBN对掘进工作面煤尘爆炸事故进行推理时,需要大量事故演变过程的数据或专家综合评价结果作为推理的先验依据。由于缺乏大量的掘进工作面煤尘爆炸事故演变过程数据,且直接运用专家综合评价结果作为推理的先验依据主观性太强,因此将基于专家综合评价结果,应用D-S证据理论预处理专家综合评价结果,再通过应用G1算法将预处理结果转化为专家权重,根据相应的专家权重确定掘进工作面煤尘爆炸事故DBN先验依据。
对D-S证据理论简要描述如下[14-15]:
设Ω为一个识别框架,在识别框架上的基本概率赋值2Ω→[0,1]的函数m,成为mass函数,并且满足:
(5)
对于任意B∈Ω,其识别框架内的有限个mass函数m1…mn的合成规则为:
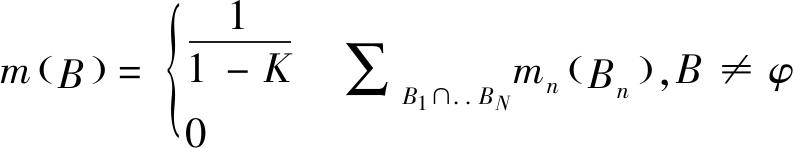
(6)
式中:K——归一化常数。
利用D-S证据理论处理后,应用G1算法确定专家权重步骤如下[16]:
(1)确定评价指标重要性排序Cn;
(2)确定评价指标相对重要程度Ri,其中Ri为Cn-1与Cn之比;
(3)计算专家权重Vj:
(7)
上述过程均由煤矿安全领域相关专家进行确定和评价,式(7)中n取15。3类不同专家的权重结果计算见表1。
表1 专家权重说明

分类说明权重人数Ⅰ矿山安全领域知名专家0.502Ⅱ副高级工程师或教授0.255Ⅲ初级职称科研人员0.158
2 动态风险分析
2.1 节点初始先验概率
在掘进工作面煤尘爆炸事故DBN中,其各节点的条件概率用来描述各节点之间的关联程度。根节点先验概率是将专家综合评价所得分数转化为专家权重并依据式(8)根节点先验概率计算公式计算得出:
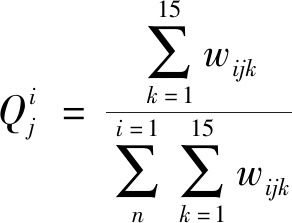
(8)
式中:![]() 风险因素j状态为i时概率,即根节点先验概率;
风险因素j状态为i时概率,即根节点先验概率;
i——风险因素的第i个状态;
n——风险因素的状态个数;
j——风险因素个数;
wijk——风险因素j的状态i发生的第k个专家对应的权值系数。
中间节点先验概率由专家综合评价结果转化为专家权重后,结合式(9)联合概率公式计算得出:
(9)
式中:P(Y)——中间节点先验概率;
P(Y|An)——An条件下发生Y的概率。
对于掘进工作面煤尘爆炸事故DBN,其各节点在初始网络的先验概率称为初始先验概率。掘进工作面煤尘爆炸事故DBN初始先验概率如图1所示。
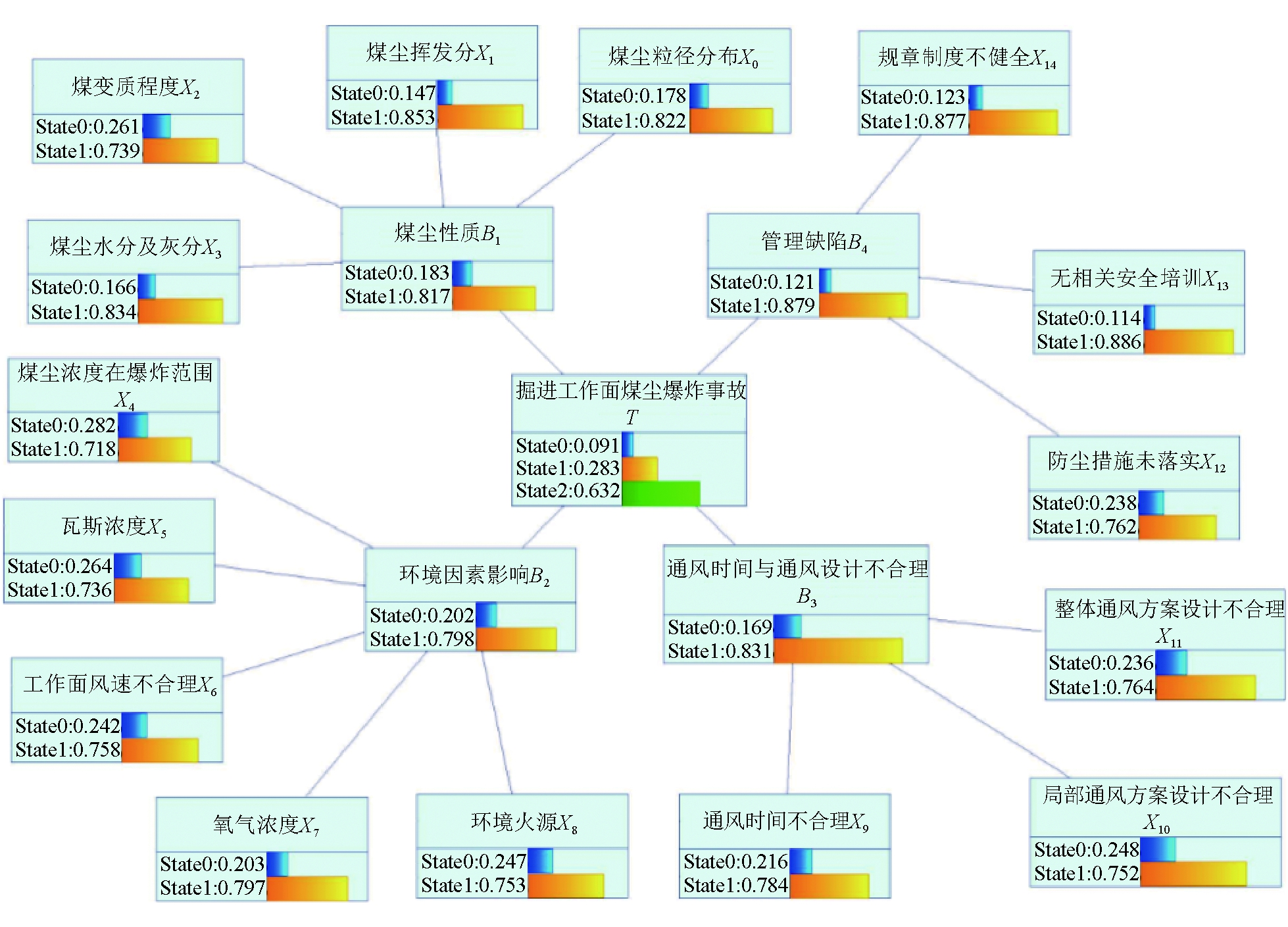
图1 掘进工作面煤尘爆炸事故DBN初始先验概率
由图1可知,掘进工作面煤尘爆炸事故造成严重后果的初始先验概率为0.090,造成较轻微后果的先验概率为0.280,后果可忽略不计的先验概率为0.630。对于各根节点先验概率,最大的为煤尘浓度在爆炸范围X4(0.282),最小的为无相关安全培训X13(0.114)。对图1中各节点先验概率数据进行分析可知,掘进工作面煤尘爆炸事故严重后果,轻微后果与后果忽略不计的概率分布与海因里希安全法则——即大量后果忽略不计和轻微后果的意外事件必将导致重大伤亡事故发生相符合。同时,依据先验概率初步判断影响掘进工作面煤尘爆炸事故发生的最大二级节点为环境因素影响B2,最小为管理缺陷B4。在4个不同二级风险因素下,对影响各个二级风险因素发生的最大的基本风险因素分别为煤尘爆炸性指数、煤尘浓度在爆炸范围、局部通风方案设计不合理、防尘措施未落实。
从初始先验概率角度对这4个基本风险因素进行分析,煤尘爆炸性指数越高,煤尘爆炸的风险越大。而掘进工作面煤尘浓度如果在爆炸范围,往往是导致掘进工作面发生煤尘爆炸事故的直接原因之一。局部通风方案设计一般是在掘进工作面施工之前就已经完成,但由于掘进工作面施工是一个动态过程,因此局部通风方案设计与掘进工作面实际生产施工之间存在滞后性,进而导致局部通风方案设计不合理,从而可能导致掘进工作面煤尘爆炸事故的发生。防尘措施未落实会进一步导致掘进工作面附近煤尘积聚,在一定条件下可引发煤尘爆炸事故。
2.2 节点先验概率预测
由于掘进工作面煤尘爆炸事故DBN中的各节点概率会随时间发生变化,且各节点的转移过程符合马尔科夫过程[17],因此对于掘进工作面煤尘爆炸事故的先验概率预测结果,可将专家经验转化为时间权重结合马尔科夫过程进行判定[18-19]。掘进工作面煤尘爆炸事故DBN转移概率公式为:
(10)
式中:t——时间片;
Si——节点X处于状态i的个数;
Si,k——节点X有状态i到状态k的个数。
时间权重计算公式为:
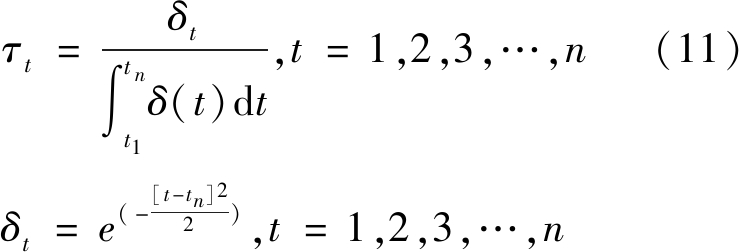
(12)
式中:τt——第t个时刻时间权重;
δt——时间折现系数。
将节点的转移过程设置为6个时间片(t=0~5),叶节点T即掘进工作面煤尘爆炸事故的3种状态在6个时间片内概率变化过程,如图2所示。
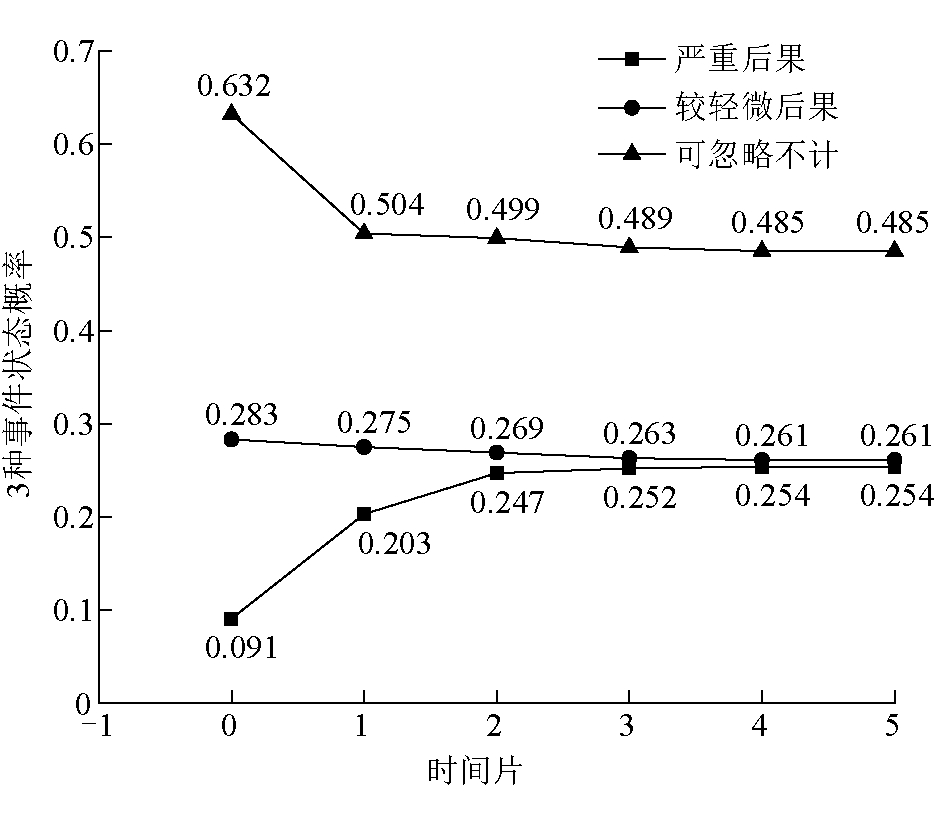
图2 叶节点T的3种状态概率变化
由图2可以看出,在6个时间片内,事故造成可忽略不计后果和较轻微后果的状态概率均有所下降。其中造成可忽略不计后果的状态概率在t=0~1时间片内显著下降,下降了0.128;在t=1~5时间片内下降缓慢,下降了0.019,并最终趋于0.485这一定值。造成较轻微后果的状态概率在t=0~1时间片内下降了0.008;在t=1~5时间片内下降了0.014,并最终趋于0.261这一定值。造成严重后果的状态概率则在t=0~1时间片内显著上升,上升了0.112;在t=1~5时间片内上升缓慢,上升了0.050,并最终趋于0.254这一定值。同时,与不同状态的初始先验概率进行对比,可知掘进工作面煤尘爆炸事故发生严重后果的状态概率相较于初始先验概率上升了0.160,发生较轻微后果的状态概率相较于初始先验概率下降0.022,事故后果忽略不计的状态概率相较于初始先验概率下降了0.147,这与图2中所示变化趋势相对应。
利用DBN正向预测各根节点事件(X0~X14)发生先验概率在6个时间片后的结果分别为0.221、0.181、0.268、0.259、0.293、0.304、0.352、0.301、0.350、0.323、0.329、0.285、0.274、0.170、0.154。预测对掘进工作面煤尘爆炸事故造成严重后果和较轻微后果的状态概率影响最大的2个基本风险因素是工作面风速不合理(0.352)和环境火源(0.350),影响最小的基本风险因素是规章制度不健全(0.154)。在4个不同二级风险因素下,对各个二级风险因素事件发生概率影响最大的基本风险因素分别是煤尘爆炸性指数(0.268)、工作面风速不合理(0.352)、局部通风方案设计不合理(0.329)、防尘措施未落实(0.274)。
通过对图2与根节点先验概率结果的分析,综合考虑各基本风险因素预测结果与掘进工作面煤尘爆炸事故3种状态概率变化情况,初步确定对掘进工作面煤尘爆炸事故造成严重后果影响最大的6个基本风险因素分别为煤尘爆炸性指数、工作面风速不合理、瓦斯浓度、环境火源、局部通风方案设计不合理、防尘措施未落实。
3 事故预防决策分析
3.1 根节点后验概率预测
直接由初始先验概率经转移网络预测所得出的各个风险因素的事件发生概率结果仍具有一定的主观性,为进一步减小主观性和对预测结果进行验证,利用后验概率公式并结合DBN进行逆推理,得出各根节点后验概率并对预测结果进行修正。DBN根节点后验概率计算公式为:
(13)
根据图2所示,在未采取任何预防措施前提下,掘进工作面煤尘爆炸事故后果忽略不计状态概率与较轻微概率均有所下降,而造成严重后果状态概率将上升。因此后验概率主要讨论掘进工作面煤尘爆炸事故造成严重后果状态时各节点后验概率。
将叶节点即掘进工作面煤尘爆炸事故T造成严重后果状态概率值设置为1.000,结合式(10)~式(13),预测各根节点(X0~X14)在6个时间片(t=0~5)后在煤尘爆炸事故T造成严重后果的状态下,事件发生的后验概率结果分别为0.231、0.183、0.272、0.260、0.289、0.302、0.348、0.304、0.353、0.318、0.332、0.288、0.271、0.173、0.154。
由节点后验概率结果可知,根节点煤尘粒径分布X0与整体通风方案设计不合理X11后验概率相较于先验概率上升了0.010,局部通风方案设计不合理X10与环境火源X8后验概率相较于先验概率提升了0.003。各根节点后验概率预测值与先验概率预测结果基本一致,验证了先验概率对于各根节点预测结果的准确性。
综合对各根节点先验概率与后验概率预测结果分析,对初步选取的6个基本风险因素进行修正,最终确定对掘进工作面煤尘爆炸事故造成严重后果的5种基本风险因素分别为瓦斯浓度、环境火源、通风时间不合理、局部通风方案设计不合理与防尘措施未落实。
3.2 单因素作用分析
由于DBN后验概率公式具有双向性,因此通过DBN后验概率公式的双向性可知,叶节点T在单个基本风险因素发生条件下的后验概率计算公式为:
(14)
由DBN推理双向性,可通过已获得的最终确定的5种基本风险因素先验概率、后验概率,结合式(10)~式(12)和式(14),对在单因素发生条件下导致掘进工作面煤尘爆炸事故造成严重后果的后验概率(P(T=0|Xi=0))结果进行计算和预测,6个时间片内预测结果:X5为0.252、X8为0.251、X9为0.254、X10为0.255、X12为0.253。不同单因素作用条件下在6个时间片内造成掘进工作面煤尘爆炸事故严重后果的概率变化过程如图3所示。
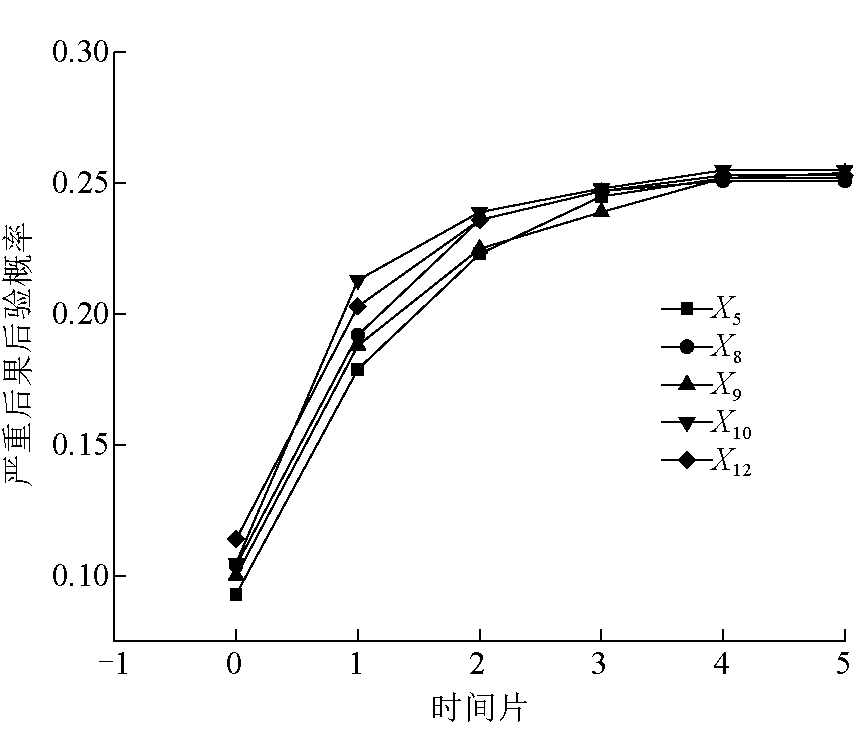
图3 单因素发生条件下严重后果后验概率变化情况
综合图3和6个时间片内预测结果可知,对所选取的5种基本风险因素,在单个风险因素发生的条件下,预测在6个时间片后,掘进工作面煤尘爆炸严重后果后验概率最大为0.255,最小为0.251。且掘进工作面煤尘爆炸事故造成严重后果的后验概率变化趋势均是初期先急剧上升(t=0~2),后缓慢上升(t=2~4),最后趋于某一定值(t=4~5)。局部通风方案设计不合理的发生对于掘进工作面煤尘爆炸事故造成严重后果的影响最大,使其后验概率预测结果相对先验概率预测结果提升了0.005。通过DBN双向综合分析,最终确定对掘进工作面煤尘爆炸事故造成严重后果状态影响最大的基本风险因素为局部通风方案设计不合理。
3.3 多因素耦合作用分析
不同组合条件下多个基本风险因素耦合作用结果计算公式:
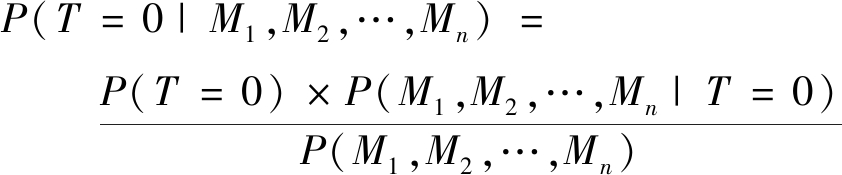
(15)
由于掘进工作面煤尘爆炸事故造成严重后果往往是多个基本风险因素耦合作用的结果,且每个基本风险因素是否发生都是相互独立的。因此将所选取的5种基本风险因素进行组合,结合DBN双向推理性,通过已获得的最终确定的5种基本风险因素的先验概率、后验概率,并结合式(10)~式(12)与式(15),对多因素耦合作用条件下掘进工作面煤尘爆炸事故造成严重后果状态的后验概率进行计算与预测,6个时间片内不同组合条件下的多种基本风险因素耦合作用导致掘进工作面煤尘爆炸事故造成严重后果的预测结果的最大值见表2,基本风险因素耦合作用结果最大值的概率变化过程如图4所示。
表2 不同组合条件下基本风险因素耦合作用结果最大值

因素组合P(T=0|M1..Mn)因素组合P(T=0|M1..Mn)(X9X10)0.256(X8X9X10X12)0.264(X9X10X12)0.259(X5X8X9X10X12)0.266
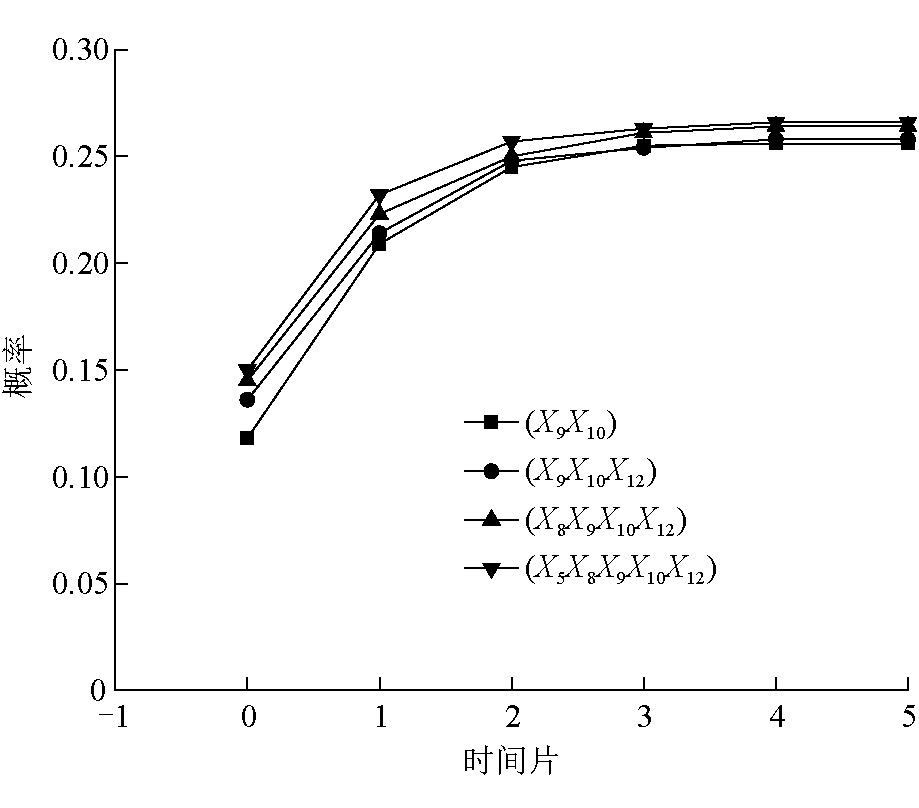
图4 基本风险因素耦合作用结果最大值的概率变化
由表2可知,预测在6个时间片内,2种因素组合条件下通过基本风险因素耦合作用,导致掘进工作面煤尘爆炸事故发生严重后果后验概率最小,为0.256;在5种因素组合条件下通过基本风险因素耦合作用,导致掘进工作面煤尘爆炸事故发生严重后果后验概率最大,为0.266。由图4可知,不同组合条件下基本风险因素耦合作用导致掘进工作面煤尘爆炸事故发生严重后果的初始后验概率也略有不同,其中5种因素组合条件下初始后验概率最大,而2种因素组合条件下初始后验概率最小。
由表2和图4综合分析可知,掘进工作面煤尘爆炸事故发生严重后果的后验概率变化情况均是初期先急剧上升(t=0~2),后缓慢上升(t=2~4),最后趋于某一定值(t=4~5)。因此对掘进工作面煤尘爆炸事故,其事故预防重点应是在事故发展初期对瓦斯浓度、环境火源、通风时间不合理、局部通风方案设计不合理与防尘措施未落实这5种基本风险因素采取相关措施,防止这5种基本风险因素同时发生。若在事故初期无法采取相关措施防止这5种基本风险因素同时发生,则应在事故发展初期采取相关措施防止表2中所列出的其他3种因素组合中的基本风险因素同时发生,以降低掘进工作面煤尘爆炸事故最终发展成严重后果的风险。
4 结论
(1)结合实际生产事故案例,建立掘进工作面煤尘爆炸DBN事故分析模型,并利用DBN进行正向推理,得出掘进工作面煤尘爆炸事故3种不同状态的初始先验概率分别为0.090、0.280、0.630;由初始先验概率结果结合式(10)~式(12)计算可知,在6个时间片后3种状态概率分别为0.254、0.261、0.485。
(2)利用DBN进行逆向推理,最终确定对掘进工作面煤尘爆炸事故造成严重后果影响最大的5种基本风险因素分别为瓦斯浓度、环境火源、通风时间不合理、局部通风方案设计不合理与防尘措施未落实。由计算可知,其后验概率预测结果与先验概率预测结果基本一致,分别为0.302、0.353、0.318、0.332、0.271。同时,在单因素作用条件下,最终确定对掘进工作面煤尘爆炸事故造成严重后果影响最大的基本风险因素为局部通风方案设计不合理。
(3)通过多因素耦合作用分析,预测掘进工作面煤尘爆炸事故造成严重后果状态概率变化情况为先急剧上升,后缓慢上升,最后趋于某一定值;在5种因素组合条件下耦合作用结果导致掘进工作面事故造成严重后果的后验概率最大,为0.266;掘进工作面煤尘爆炸事故造成严重后果的预防重点是在事故发展初期对所选取的5种因素采取相关措施防止这5种基本风险因素同时发生。
[1] 王可.受限空间内煤尘爆炸及抑爆特性研究[D].徐州:中国矿业大学,2016.
[2] 景国勋,彭乐,班涛.煤质指标对煤尘爆炸最大压力上升速率的影响[J].煤矿安全,2020,51(1):42-46.
[3] 裴蓓,朱知印,余明高,等.瓦斯/煤尘爆炸初期复合火焰加速及灾害强化机制分析[J].工程热物理学报,2021,42(7):1879-1886.
[4] ZHANG Leilin,YANG Qianyi,SHI Biming,et al.Influences of a Pipeline's Bending Angle on the Propagation Law of Coal Dust Explosion Induced by Gas Explosion[J].Combustion Science and Technology,2021,193(5).
[5] 王文和,董传富,刘林精,等.基于贝叶斯网络的城市地下燃气管网动态风险分析[J].中国安全生产科学技术,2019,137(5):55-62.
[6] 李爽,李丁炜,犹梦洁.煤矿安全态势感知预测系统设计及关键技术[J].煤矿安全,2020,51(5):244-248.
[7] 高涵,多依丽,孙铁,等.基于DBT-DBN模型的气化炉超温动态风险分析[J].中国安全科学学报,2021,31(3):73-81.
[8] 谢小良,褚琦,张淑君,等.基于DBN的疫苗运输质量安全风险监测方法[J].中国安全科学学报,2020,30(7):19-26.
[9] WU S,ZHANG L,ZHENG W,et al.A DBN-based risk assessment model for prediction and diagnosis of off-shore drilling incidents[J].Journal of Natural Gas Science and Engineering,2016,34:139-158.
[10] XIANG W,ZHOU W.Integrated pipeline corrosion growth modeling and reliability analysis using dynamic Bayesian network and parameter learning technique[J].Structure and infrastructure engineering,2020,16(8):1161-1176.
[11] WANG Y F,QIN T,LI B,et al.Fire probability prediction of offshore platform based on dynamic Bayesian network[J].Ocean Engineering,2017,145:112-123.
[12] 国家煤矿安全监察局办公室.国家煤矿安全监察局关于山东能源肥城矿业集团梁宝寺能源有限责任公司“8·20”煤尘炸事故的通报[R].北京:国家煤矿安全监察局,2020.
[13] 陈慧慧,施书磊,郑明亮.基于模糊事故树的煤尘爆炸事故分析[J].煤炭技术,2018,37(8):180-182.
[14] JIANG W,XIE C,ZHUANG M Y,et al.Failure mode and effects analysis based on novel fuzzy evidential method[J].Applied Soft Computing,2017,57:672-683.
[15] 陈军,兀亚伟,李垣志,等.基于动态贝叶斯网络的燃气管网燃爆风险分析[J].北京理工大学学报,2021,41(7):696-705.
[16] 郭平,任康飞,高明,等.基于WSR-云模型的保障性住房PPP项目建设风险评价[J].西安建筑科技大学学报(社会科学版),2021,40(5):85-92.
[17] RIDI A,HENNEBERT J.Hidden Markov models for ILM appliance identification[J].Procedia Computer Science,2014,32:1010-1015.
[18] 丁保军,吴贤国,张立茂,等.基于DBN的盾构隧道施工参数优化方法研究[J].岩石力学与工程学报,2015,34(S1):3215-3222.
[19] WU X G,LIU H T,ZHANG L M,et al.A dynamic Bayesian network based approach to safety decision support in tunnel construction[J].Reliability Engineering &System Safety,2015,134:157-168.
Risk prediction of coal dust explosion accident in heading face based on dynamic Bayesian network

- 相关推荐
