基于多传感器信息融合的煤与瓦斯突出预警模型研究
时间:2024-08-20 来源:中国煤炭杂志官网 分享:★ 煤矿安全 ★
基于多传感器信息融合的煤与瓦斯突出预警模型研究
0 引言
煤与瓦斯突出是煤矿井下采掘过程中的一种复杂的动力现象,是我国最严重的煤矿灾害之一[1-2]。矿井瓦斯安全监测与灾害预警是有效防治煤与瓦斯突出、减少人员伤亡的重要措施。近年来,随着我国煤矿监测预警技术的迅猛发展,单一传感器监测预警已无法适应煤矿井下复杂的环境[3-4],集成化、智能化、数字化已成为瓦斯突出预警系统发展的新方向[5-6]。通过多传感器数据融合技术对不同种类(如瓦斯、温度、风速等)的信息进行综合分析,为提高煤矿瓦斯安全监测与灾害预警系统的可靠性和智能化水平提供了新途径[7]。
目前,我国的专家学者在煤矿安全监测预警领域已开始研究与应用多传感器数据融合技术。潘泉等[8]通过结合多传感器的算术平均值和分批估算法得到了比传统预测方法更准确的结果;张保东[9]通过多类传感器采集瓦斯浓度、通风、煤岩动力等瓦斯灾害信息参数,设计了一种基于模糊专家系统的瓦斯突出预测决策级融合方法;宁小亮[10]采用关联规则算法和证据理论算法相结合的方法,建立了煤与瓦斯突出动态预警模型。现阶段构建的预警模型融合度不高、相对固化、自分析与优化能力不足,预警的智能化水平还有待提高。本文结合实际矿井瓦斯抽采环境,利用多传感器数据融合理论,构建了一种煤与瓦斯突出预警模型,并且调用合适的信息融合算法在预警模型的各个层次实现煤与瓦斯突出预警,从而提高煤矿瓦斯预警水平,保障煤矿井下的安全生产。
1 煤与瓦斯突出指标与因素分析
1.1 煤与瓦斯突出预测指标确定
目前,国内外的专家们从不同的角度对煤与瓦斯突出的影响因素进行了深入的研究,并提出了各种影响指标和突出敏感指标的临界值。这些影响因素被分类为静态指标和动态指标,静态指标法包括单项指标法、综合指标D和K法;动态指标法包括温度指标、弹性波速指标及瓦斯涌出动态指标等[11-12]。
本文将动态指标和静态指标相结合,根据煤与瓦斯突出影响因素及其指标,选择合适的测量传感器,准确地获取指标参数值。煤与瓦斯突出指标确定过程如图1所示。通过将权重较大的指标,如综合指标D/K、瓦斯涌出初速度q、最大钻屑量S,作为特征层的不同特征进行数据处理融合,而将权重较小的指标,如巷道类型、垂深(开采深度)、煤层厚度、倾角、地质构造、作业方式等,作为神经网络预测法的输入参数,利用神经网络的高度非线性映射关系建立煤与瓦斯突出预测模型。
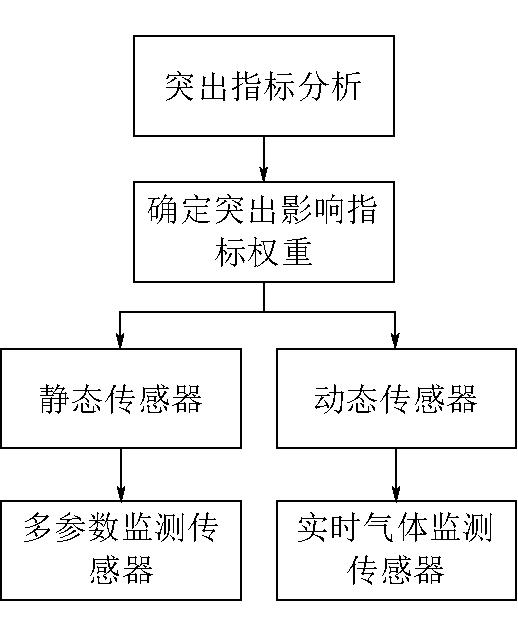
图1 煤与瓦斯突出指标确定过程
1.2 煤与瓦斯突出影响因素权重分析
通过分析影响煤与瓦斯突出的因素,构建了层次分析模型并计算了权重排序向量。权重排序向量可以清楚地显示各因素的权重大小,量化影响煤与瓦斯突出的定性指标。
(1)影响因素选择。本研究选择了具有代表性的因素来分析煤与瓦斯突出的风险,包括煤层的垂直深度H、煤层厚度M、煤层倾角α、地质构造T、巷道类型Y、钻孔瓦斯涌出的初始速度q、综合指标D/K、最大钻屑量S、作业方式Z等9种指标。
(2)建立判断矩阵。试验地点为贵州省新田煤矿,由具有相关经验的技术人员和专家确定上述影响因素的标度,通过比较各因素的重要程度,构建了煤与瓦斯突出各影响因素的判断矩阵,见表1。
表1 煤与瓦斯突出影响因素判断矩阵
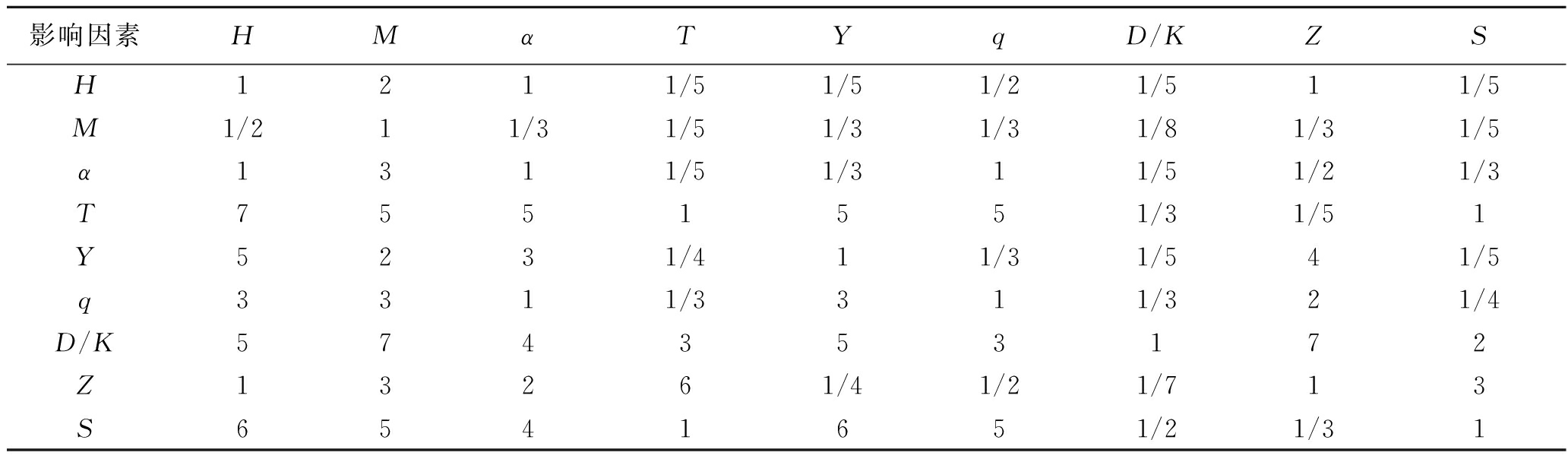
影响因素HMαTYqD/KZSH1211/51/51/21/511/5M1/211/31/51/31/31/81/31/5α1311/51/311/51/21/3T7551551/31/51Y5231/411/31/541/5q3311/3311/321/4D/K574353172Z13261/41/21/713S6541651/21/31
(3)求判断矩阵的特征值和特征向量。采用层次分析法计算特征值λmax和特征向量Wi。计算判断矩阵每一行元素的乘积Mi,见式(1);计算Mi的n次方根并对向量![]() 正规化,见式(2):
正规化,见式(2):
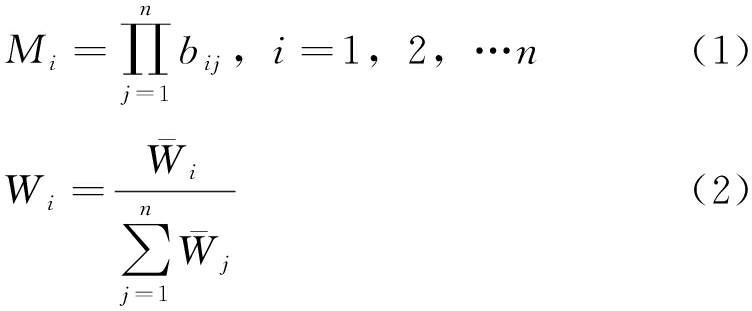
式中:Mi——元素的乘积;
bij——元素矩阵中单个元素值;
![]() 各行向量均值;
各行向量均值;
![]() 各行单个元素向量均值;
各行单个元素向量均值;
Wi——正规化后向量值。
由式(1)和式(2)计算判断矩阵的最大特征值λmax=7.783 5。
(4)一致性检验。依据层次分析法的随机一致性指标RI值选取并结合表1影响因素对比值计算一致性指标RI,可以得出一致性指标CI=0.153,RI=1.42,CR=0.091 8≤0.1,满足一致性要求,因此可以用特征向量Wi作为权重向量。
(5)权重向量排序。根据上述的步骤求出特征向量Wi,可以得出各指标因素的权重大小不同,即对煤与瓦斯突出危险性的影响程度有明显的差异。
为了明确表征各特征因素对煤与瓦斯突出影响大小,经计算后对特征向量Wi进行权重系数排序,影响煤与瓦斯突出因素的权重及其权重系数由大到小依次为:综合指标D/K(0.352)、地质构造T(0.368)、最大钻屑指标S(0.320)、钻孔瓦斯涌出初速度q(0.112)、煤层垂直深度H(0.096)、煤层倾角α(0.082)、作业方式Z(0.075)、巷道类型Y(0.070)和煤层厚度M(0.041)。预测煤与瓦斯突出时,需要参考选取因素的权重系数进行判断。
2 多传感器信息融合煤与瓦斯突出预测模型
2.1 模型建立
基于多传感器信息融合的煤与瓦斯突出预测模型如图2所示。预测模型由监测传感器子系统、特征级信息融合处理子系统、信息管理及决策支持子系统、传感器管理系统4部分构成。在广域的矿井瓦斯监测环境系统中,利用计算机按照时序采集不同类别、不同传感器的监测信息,并在一定的准则下自动分析和综合处理相关信息数据,实现对煤与瓦斯突出状况的信息处理,然后依据处理后的信息做出相关决策。在模型构建的系统中监测的不同多传感器及信息广域网络环境系统是数据融合的硬件基础,而多源信息则成为数据融合的加工对象,协调管理和综合处理是数据融合的核心。
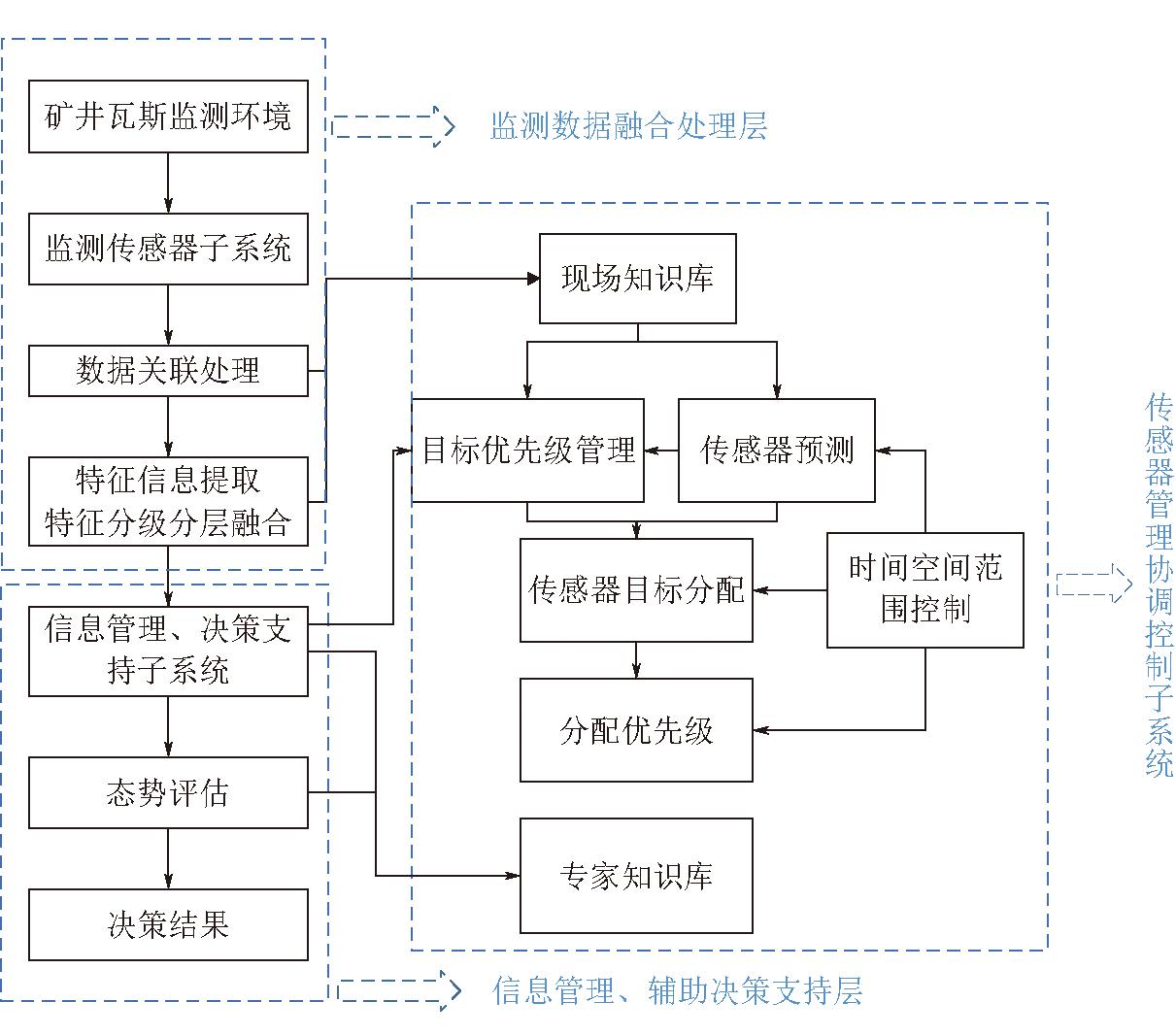
图2 基于多传感器信息融合的煤与瓦斯突出预测模型
2.2 分层多传感器信息融合方法
在研究和分析各种多传感器信息融合算法以及各个层次的融合方法时,通常选用深度神经网络作为特征层的多传感器融合方法。本模型采用了无监督学习的反向传播算法,改进了传统的BP神经网络算法,利用深度自动编码器进行信息识别,多信息融合方法如图3所示。考虑到神经网络本身的局限性,本研究提出了以D-S证据理论作为决策级的融合方法,构成了特征级和决策级的分层融合结构,以提高决策的可靠性。
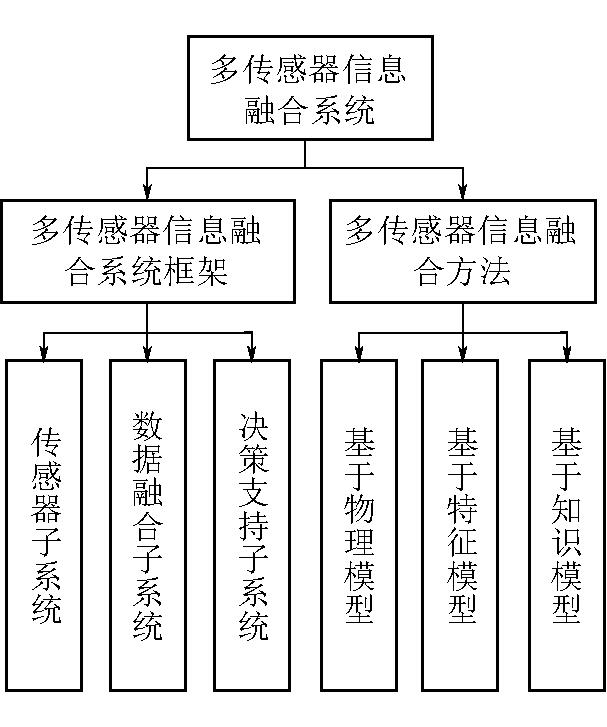
图3 多信息融合方法
3 工作面突出预测指标应用
3.1 矿井工作面突出预测数据
本文以永贵能源开发有限责任公司新田煤矿(以下简称“新田煤矿”)某一掘进工作面预测孔的钻屑瓦斯解析指标Δh2、钻孔瓦斯涌出初速度q和钻屑量S进行预测分析。选取3月1-30日内的突出预测指标跟踪考察值进行分析,见表2。
表2 工作面突出预测指标监测
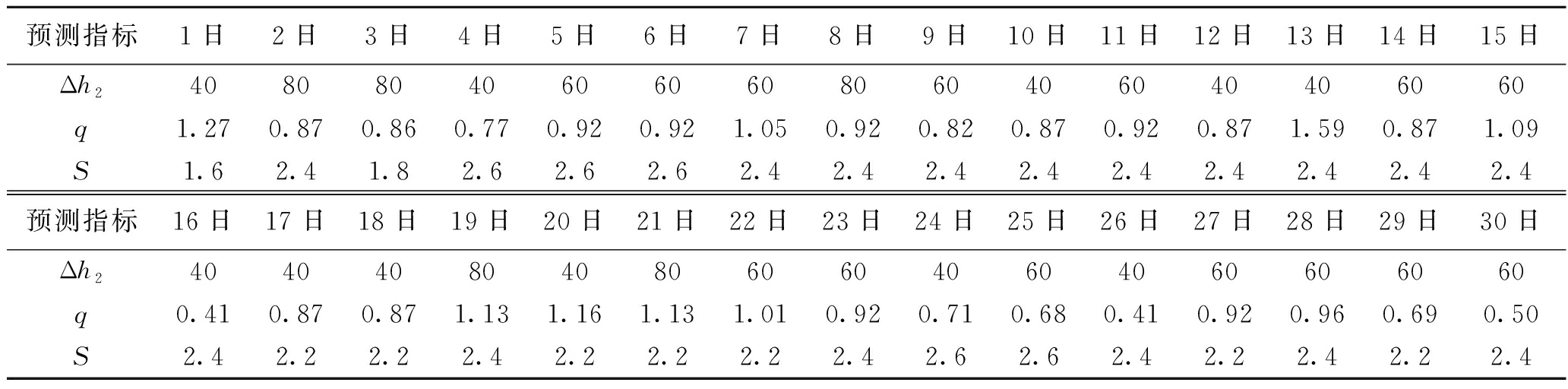
预测指标1日2日3日4日5日6日7日8日9日10日11日12日13日14日15日Δh2408080406060608060406040406060q1.270.870.860.770.920.921.050.920.820.870.920.871.590.871.09S1.62.41.82.62.62.62.42.42.42.42.42.42.42.42.4预测指标16日17日18日19日20日21日22日23日24日25日26日27日28日29日30日Δh2404040804080606040604060606060q0.410.870.871.131.161.131.010.920.710.680.410.920.960.690.50S2.42.22.22.42.22.22.22.42.62.62.42.22.42.22.4
3.2 突出指标预测分析
自回归移动平均模型ARMA(p,q)是目前应用最为广泛的平稳序列拟合模型,具体分为AR(p)、MA(q)、ARMA(p,q)3种类型。自回归模型AR(p)模型是简化的ARMA模型,模型表达见式(3):
Yt=φ1Yt-1+φ2Yt-2+…+φpYt-p+et
(3)
式中:φ1,φ2,…,φp——回归系数;
et——误差值,其均值为0;
Yt——不同阶段观测值;
p——回归阶数,即模型中解释变量的个数。
式(1)称为p阶自回归模型。
采用最小二乘法对AR(p)模型进行参数估计,已知样本序列X1,X2,…,Xn,将式(3)构建成矩阵形式见式(4)和式(5):
y=-Xϑ+e
(4)
其中
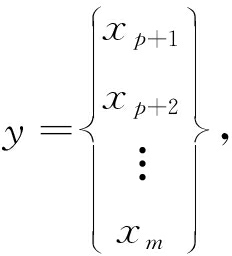 ϑ
ϑ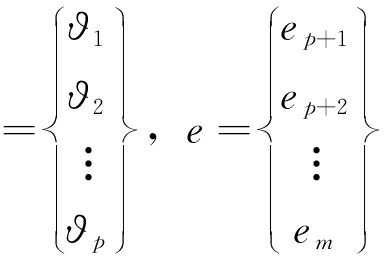
(5)
式中:ϑ——估计系数;
e——误差值;
y——估计值;
xm——样本值。
使估计系数统计值S(ϑ)=min{S(ϑ)},此时ϑ为最小二乘估计,由最小二乘估计的运算方法可得ϑ的最小二乘估计见式(6)和式(7):
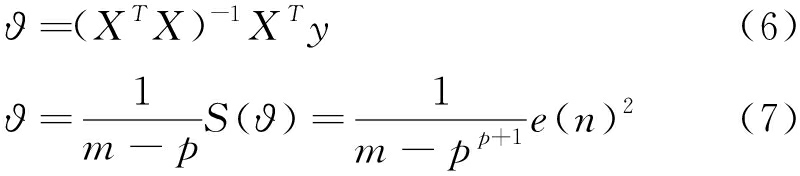
式中:S(ϑ)——估计系数统计值;
e(n)——误差向量值;
m——样本序列个数。
对未来的数据进行预测,计算出相对误差及平均误差率:
(8)
式中:q——相对误差,其平均值即为误差平均率;
qs——统计值;
qr——统计预测值。
依据表2的预测指标,利用SPSS软件中时间序列模型对其前27 d的数据进行模型构建,并预测之后3 d的数据,同实际数据进行对比,验证模型的准确性。
通过对AR模型进行仿真,使阶数p=0开始依次递增,分析模型的残差自相关图与残差偏自相关图的截尾与拖尾状态,当构建的工作面突出预测指标AR(p)模型与原始序列较为一致时,即满足仿真要求,确定p的值。
突出预测指标模型残差自相关与偏自相关系数如图4所示。由图4可知,当p=3时,仿真序列与原始序列较一致,即AR(3)模型参数比较准确。
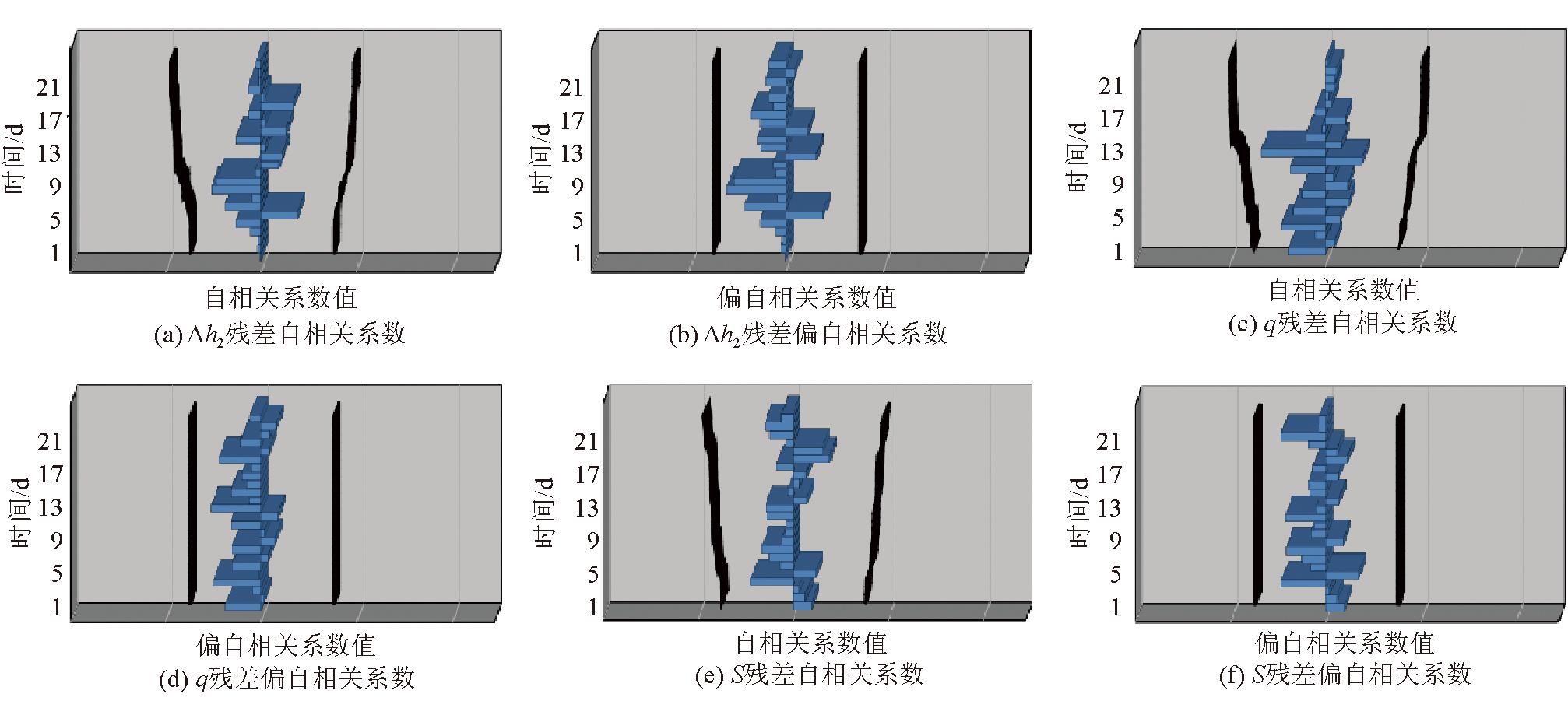
图4 突出预测指标模型残差自相关与偏自相关系数
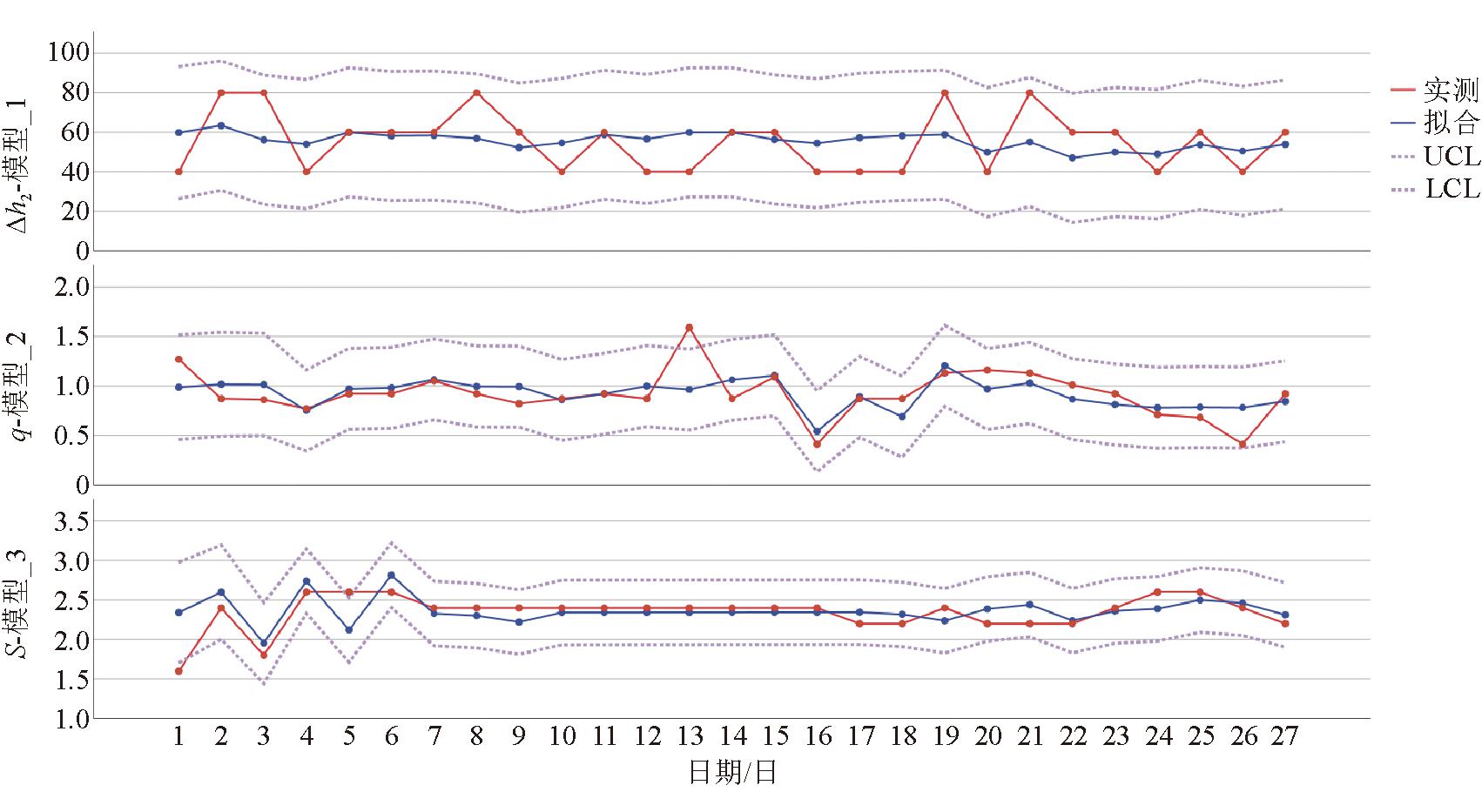
图5 AR模型预测对比
指标的自回归模型AR(3)模型实测值与预测值拟合曲线如图 5 所示。由图 5 可以看出,指标预测值曲线与实测值曲线的拟合度较高,可以准确地反映钻屑瓦斯解析指标Δh2、钻孔瓦斯涌出初速度q和钻屑量S的变化趋势,效果良好且预测值均处在置信区间内。指标预测值与实际值对比见表3。结合表 3 中的预测结果可知,Δh2预测的最大绝对误差为2,最大相对误差为 3.0%,最小绝对误差为 0,最小相对误差为0;q预测的最大绝对误差为0.04,最大相对误差为 8.0%,最小绝对误差为 0.02,最小相对误差为2.1%;S预测的最大绝对误差为0.1,最大相对误差为 4.5%,最小绝对误差为 0,最小相对误差为0,实测值与预测值的绝对误差与相对误差较小,由此说明,AR(3)模型可以用于突出指标的预测,且预测精度较高。
表3 指标预测值与实际值对比

日期Δh2实际值/Pa预测值/Pa绝对误差/%相对误差q实际值/(L·min-1)预测值/(L·min-1)绝对误差相对误差/%S实际值/(L·min-1)预测值/(L·min-1)绝对误差相对误差/%28日605823.00.960.940.022.12.42.40029日6060000.690.720.034.22.22.30.14.530日606223.00.500.540.048.02.42.400
4 结论
(1)以煤矿监控系统的数据流动特点为基础,结合多传感器信息融合技术,研究了多传感器信息融合下的煤与瓦斯突出预警,构建一种基于数据融合的瓦斯突出指标预警模型。
(2)基于动态和静态传感器多参数监测分析,采用层次分析法计算突出影响因素权重,依据权重系数大小确定突出预测指标。
(3)依据选取的突出指标构建了由监测传感器子系统、特征级信息融合处理子系统、信息管理及决策支持子系统和传感器管理系统组成的传感器信息融合煤与瓦斯突出预测模型。
(4)依据新田煤矿某工作面突出预测指标构建了自回归移动平均模型AR(3),并对指标数据进行了预测分析,结果表明,模型准确性较高,预测值与实际值误差较小,能够用于实际的突出指标预测。
[1] 袁亮.深部采动响应与灾害防控研究进展[J].煤炭学报,2021,46(3):716-725.
[2] 王恩元,张国锐,张超林,等.我国煤与瓦斯突出防治理论技术研究进展与展望[J].煤炭学报,2022,47(1):297-322.
[3] 袁亮.我国煤矿安全发展战略研究[J].中国煤炭,2021,47(6):1-6.
[4] 王恩元,李忠辉,何学秋,等.煤与瓦斯突出电磁辐射预警技术及应用[J].煤炭科学技术,2014,(6):53-57,91.
[5] 孔祥国,王恩元,胡少斌,等.含瓦斯型煤破坏临界慢化前兆特征研究[J].中国矿业大学学报,2017(1):1-7.
[6] 黄凯峰,刘泽功,王其军,等.基于ASGSO-SVR模型的瓦斯传感器故障诊断[J].煤炭学报,2013,38(S2):518-523.
[7] 姜福兴,尹永明,朱权洁,等.基于掘进面应力和瓦斯浓度动态变化的煤与瓦斯突出预警试验研究[J].岩石力学与工程学报,2014,33(S2):3581-3588.
[8] 潘泉,王增福,梁彦,等.信息融合理论的基本方法与进展[J].控制理论与应用,2012,29(10):1233-1244.
[9] 张保东.多源信息融合在煤矿瓦斯监测中的应用[J].煤矿安全,2017,48(5):137-139,143.
[10] 宁小亮.基于多源信息融合的煤与瓦斯突出动态预警模型[J].矿业安全与环保,2020,47(3):1-5,16.
[11] 李忠辉,马云波,郑安琪,等.掘进工作面突出危险性预测及危险区可视化研究[J].中国安全科学学报,2020,30(11):53-59.
[12] 卢新明,张天宇,王永,等.基于瓦斯涌出时序序列的煤与瓦斯突出离散模态预警方法[J].煤矿安全,2020,51(11):175-179.
Research on early warning model of coal and gas outburst based on multi-sensor information fusion

移动扫码阅读
CHEN Zuguo,ZHANG Ningbo,GAO Yuanyuan,et al. Research on early warning model of coal and gas outburst based on multi-sensor information fusion[J].China Coal,2024,50(6)∶67-73.DOI:10.19880/j.cnki.ccm.2024.06.009
- 相关推荐
