考虑管内压力损失及地层渗透扩散效应的顺层孔压力分布规律研究
时间:2023-07-27 来源:中国煤炭杂志官网 分享:★ 煤矿安全 ★
考虑管内压力损失及地层渗透扩散效应的顺层孔压力分布规律研究
0 引言
煤炭资源是我国的主要能源,随着开采深度的不断增加,矿井的水文地质条件越来越复杂[1-3]。矿井在受到高地应力以及复杂地质条件等因素影响下,水害突出危险性呈现出增加趋势,矿井突水事故的发生不仅造成人员的大量伤亡和巨大的财产损失,而且还会严重威胁矿井安全生产[4-9]。依据《煤矿防治水细则》中规定“对水文地质类型为复杂及以上煤矿的新水平、新采区掘进时,应当同时采用物探、钻探等方法循环探查工作面前方及顶(底)板富水情况”,而以往在煤矿井下开展的“钻探+物探”超前探查工作无法保证巷道的连续掘进,给矿井的正常生产接替造成了阻碍。基于此,采用地面定向钻进技术,在探查区域合理布孔的基础上进行地质构造异常体与工作面顶(底)板富水性的探查[10-11]。压水试验结果显示,若压水水压不小于受注段所在位置奥灰静水压力的1.5倍,稳定时间不少于30 min,且计算单位吸水率大于0.01 L/(min·m2),则表明目的层富水性较强、存在断层裂隙或陷落柱等地质异常体的可能,因此受注段所在位置实际水压值的大小是进行对比分析的前提条件,据此,开展煤矿地面区域治理探查孔压力分布规律研究,在掌握受注段实际水压的基础上,准确评价地质构造异常体存在的可能性,以实现巷道安全掘进、工作面安全回采。
近年来,国内外众多学者采用不同的研究手段对水平钻孔的孔内压力分布规律等方面进行了深入的研究。李华锋等[12]根据质量守恒及动量守恒定理推导得到了考虑压损的水平井压力计算公式;孙恩慧等[13]建立了低渗透油藏水平井流动力学分析模型,并编制了相应的求解程序;白方方等[14]基于水平井与直井流动的差异性,建立了水平井井控多相流理论分析模型,并根据现场实例参数进行了有限差分数值分析;李松泉等[15]在综合考虑井筒压降、各向异性等因素的影响下,推导得出了气藏耦合效应影响下的水平井井筒压力求解模型。笔者以上述研究成果为基础,采用理论分析结合数值分析的综合研究手段,基于伯努利方程的管路流模块与多孔介质中流体渗流的广义达西定律等模块,建立地面定向钻孔顺层压水试验模型,综合考虑各入口压力、地层渗透率以及质量流率等因素影响,在理论结果与数值结论取得相互印证的基础上,探讨了不同顺层段位置处压力的分布规律,并对不同因素影响下顺层裸孔段的压力分布规律进行了系统分析,所得结果可为顺层压水探测煤层底板构造异常体提供基础理论依据。
1 地面定向钻孔顺层压水试验数值模型
在顺层压水试验中,一开和二开为管内流动的管路流,而进入三开裸孔段之后,可将地层视为各项同性均质的地质体,其渗流问题可运用水在多孔介质中渗流的达西定律进行描述,据此采用COMSOL数值模拟软件建立顺层压水试验模型,在给定压力与流量情况下计算分析不同顺层段位置处压力的分布规律。
1.1 模型几何尺寸
顺层压水试验数值模型如图1所示,模型中包括2根不同的管路(直线段为管路1,圆弧段为管路2)和地层基体以及其内部的一条渗流通道(管路3),可分别模拟顺层压水试验中的路管1、路管2及路管3(顺层裸孔段)。
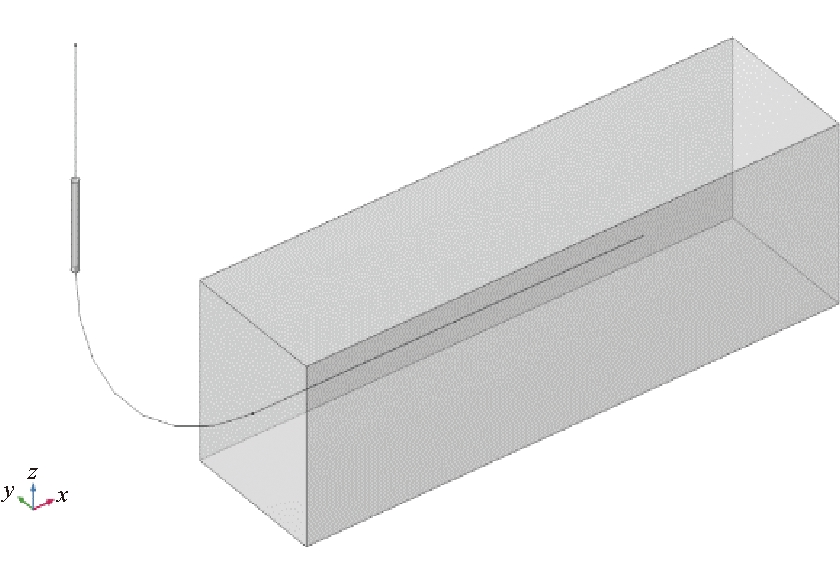
图1 顺层压水试验数值模型
数值模型中,地层孔隙率0.08,地层渗透率4.5×10-15 m2,管路1内径为0.226 2 m,长为250 m,摩擦模型采用Churchill模型,表面粗糙度为0.001 5 mm;管路2内径为0.161 7 m,长为353.55 m,表面粗糙度为0.001 5 mm;管路3为裸孔,其中地层基体尺寸为200 m×200 m×750 m,内部含有1条圆柱渗流管路,其半径为0.152 4 m,长为550 m,孔隙率1。
1.2 数值模型网格划分
为了使得出的解更容易收敛、结果更加准确,各单元之间的边和角的尺寸应当尽量接近。除此之外,网格生成器还应能在短距离内实现分级。因此在此模型中的网格选择四面体网格,单元大小使用超细化单元,单元个数为163 947个,平均单元质量为0.82,划分网格后的数值模型如图2所示。

图2 顺层压水试验数值模型网格划分
1.3 边界条件
模型中,管路1上端为压力边界条件,入口压力设置为2.5 MPa,下端与管路2的连接处使用收缩扩张的突变条件;管路2上端与管路1相连,下端与基体连接,连接处设置为出口边界条件,质量流率为2.5 kg/s;基体四周为出口边界,压力随重力变化,内部渗流通道与管路2的连接处为入口边界条件,压力为7.35 MPa。
2 数值结果分析
在如上所述的边界条件及计算参数条件下,采用Comsol Multiphysics数值模拟软件对不同管路内压力分布特征进行数值模拟分析。管路1、管路2压力分布如图3所示,管路1、管路2压力随管路长度变化关系如图4所示。
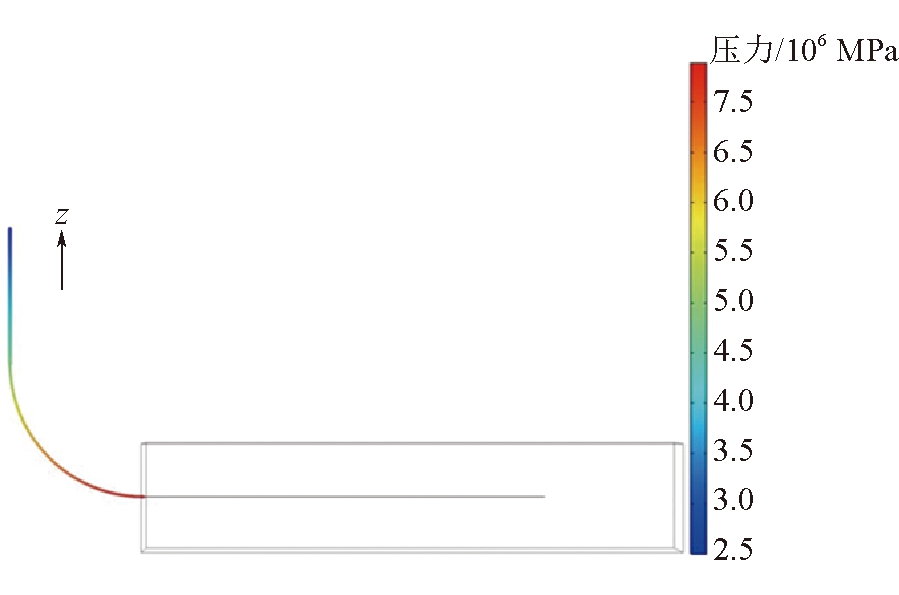
图3 管路1、管路2压力分布
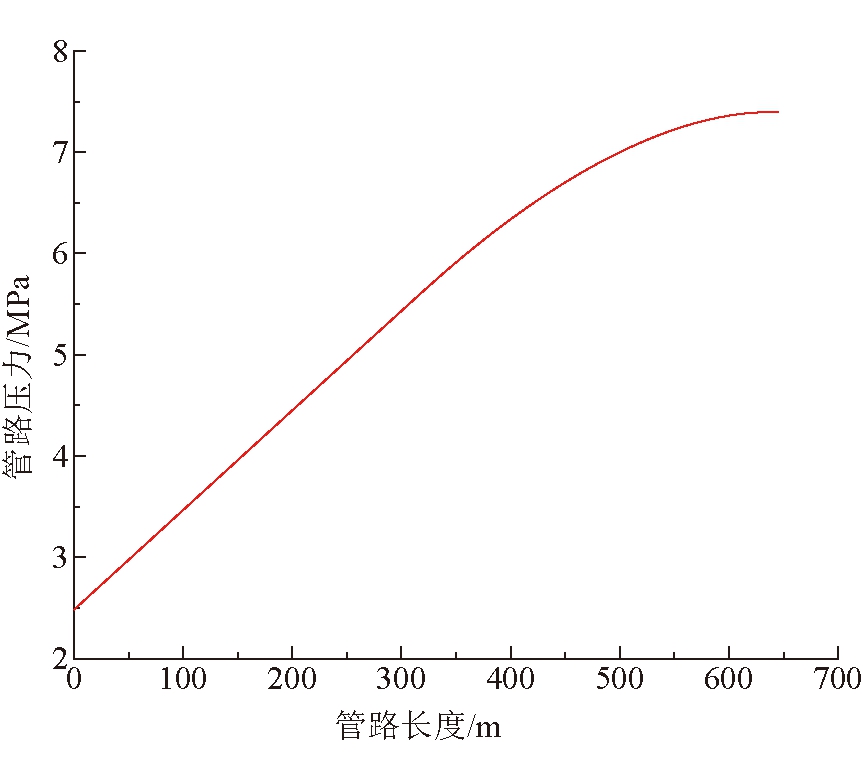
图4 管路1、管路2压力随管路长度变化关系
由图3和图4可以看出,在重力势能的影响下,管路内压力随着深度增加而增大,在管路1上端压力存在最小值2.5 MPa,而在管路2的出口端存在压力的最大值7.35 MPa。压力在竖直的管路1内受重力因素的影响沿着z轴负方向呈现线性增加趋势;在弧线状的管路2内压力增加速度变缓,呈现幂指数变化。前两段管路,重力的影响远大于管路自身因素造成的压力损失,所以压力保持增长的趋势。而管路1由于是垂直段,仅有沿程压力损失;管路2为弧线段,除沿程压力损失外,弧线段及管路接口处的局部压力损失都将对管路2的压力造成影响。
管路3压力分布如图5所示,管路3压力随管路长度变化关系如图6所示。
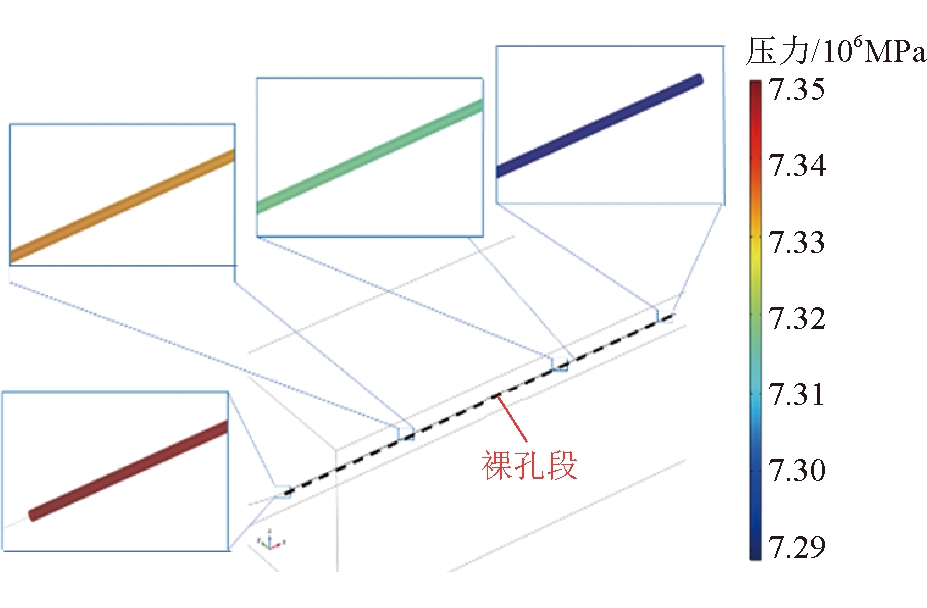
图5 管路3压力分布
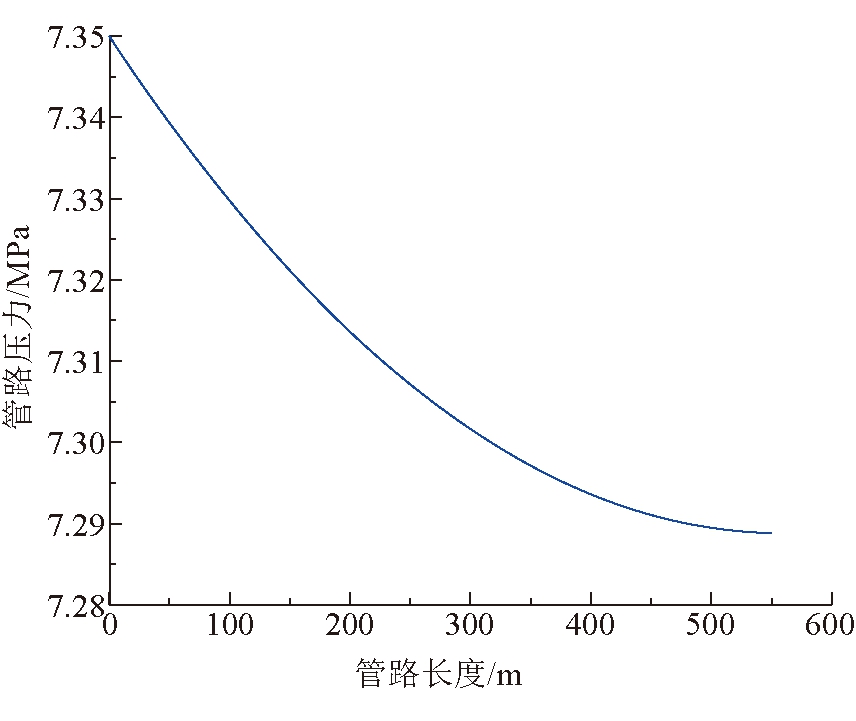
图6 管路3压力随管路长度变化关系
由图5和图6可以看出,水压在沿着管路3方向的一定范围内近似线性降低,其趋势基本符合达西线性渗流定律。管路3入口压力与管路2的出口端压力相同,为7.35 MPa,管路3末端压力为7.29 MPa。在0~275 m段内,压力降呈线性变化,在275~550 m段内变化逐渐舒缓,整体呈负幂指数变化。
压力水进入管路3后,一方面在裸孔段内进行流动,另一方面渗入地层之中。地层裸孔段压力分布如图7所示。
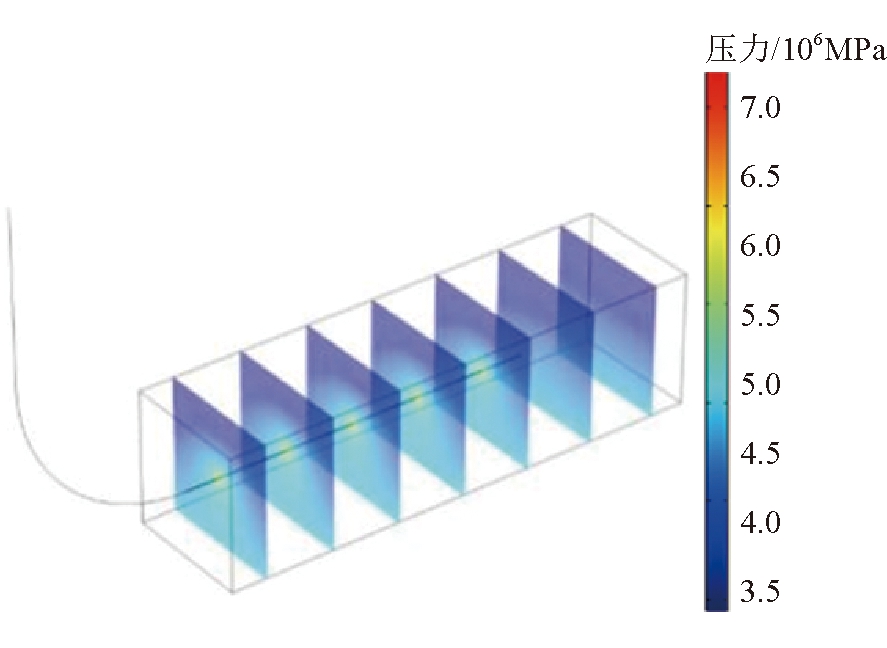
图7 地层裸孔段压力分布
由图7可以看出,流体在管路3流动的过程中,管路3内压力始终高于地层压力,在压力梯度作用下,压力水不断向地层扩散。由于沿程压力损失及向地层进行渗透的影响,管路3的入口端压力要高于出口端压力,这会导致流体在入口端附近的扩散半径要大于后半段,即随着进入管路3长度的不断增大,压力水在向地层渗流的过程中扩散半径不断减小。
由数值模拟结果可知,压力水自着陆点进入管路3后,一方面沿着裸孔段继续向前推进,另外一方面则会沿着裸露的地层进行径向扩散,且扩散半径不断减小。以该结论为概念基础采用理论分析的手段,对管路3内的压力分布特征进行理论分析。
3 三段压力分布理论分析
在将地层视为均质各向同性的基础上,径向扩散主要呈现出圆形扩散的形态,据此在充分考虑裸孔段内压力损耗的基础上,建立力学概念模型,三开段压力水渗透扩散示意如图8所示。

图8 三开段压力水渗透扩散示意
水由着陆点进入管路3之后,流量不仅分配到管路3,且在径向压力梯度的作用下会沿着地层进行径向的渗透扩散,在不考虑重力的作用下其扩散形态类似于圆形,且管内相邻部分由于径向剖面的压力梯度大体相同,可视为扩散半径相同。于此,当压水时间为t,在轴向管流与剖面径向流同时扩散后,沿着管路3切割厚度为△x的圆柱,为求出不同三开位置处的压力,以上述分析为基础,并进行如下假设:
(1)管路3周围地层为均质、各向同性介质;
(2)对于每段微元段△x的圆柱来说,其扩散过程中的流量q保持不变;
(3)不考虑顺层段的倾角影响,即忽略水在扩散过程中的重力影响。
首先以压水t时刻后,着陆点口处第1个厚度△x的圆柱微元体为研究对象,设其流量值为q1,圆柱体底界面的半径(t时间水的扩散半径)为 r,则可知:
![]() ∇p
∇p
(1)
式中:q1——流量;
k——地层渗透系数;
r——圆柱体底界面的半径(t时间水的扩散半径);
μ——水的动力黏度;
p——压力。
采用分离变量法求积分,并根据边界条件:当r=r0时,p=p1,p1为着陆点处的压力;当r=r1时,p=pc,pc为顺层裸孔段处的静水压力,将内外边界条件代入式(1)可得:
(2)
式中:p1——着陆点处的压力;
pc——顺层裸孔段处的静水压力。
对于恒定流量q1而言,t时刻后扩大的体积为:
q1t=△xφπr2
(3)
式中:φ——地层的孔隙度。
联立式(2)、式(3)可得t时刻后,第1个微元圆柱体对应截面的扩散半径r1的隐式表达式:
(4)
因此各微元段对应截面的扩散半径ri与流量qi表达式如(5)所示:
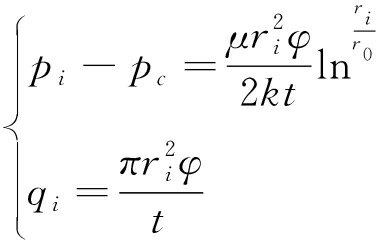
(5)
以微元段中第i段流动过程为研究对象,其流动示意如图9所示。
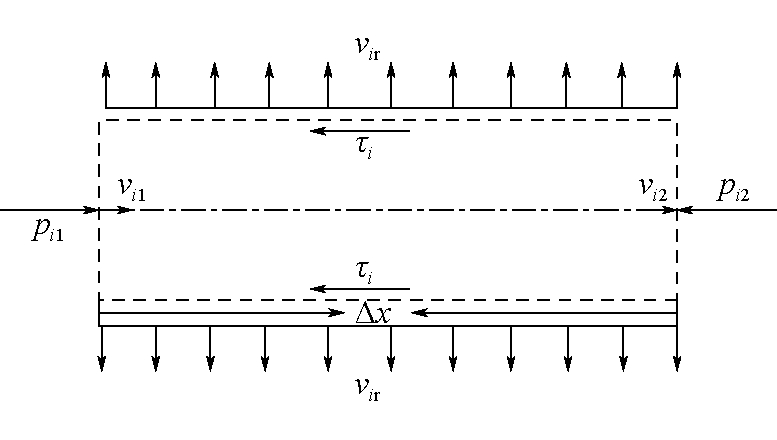
图9 第i微元段中流动示意
水在裸孔段内移动的过程由于地层渗漏的影响,是一个变质量的过程,因此其在移动过程中由质量守恒定律可知:
ρvi1A-ρvi2A-ρvirπD△x=0
(6)
式中:vi1——第i微元段轴向主流方向上游速度;
vi2——第i微元段轴向主流方向下游速度;
vir——第i微元段径向流流量值;
D——管路3的直径;
A——裸孔段截面积。
由微元段的动量守恒可知:
Pi1A-Pi2A-τiπD△x=ρvi2Avi2-ρvi1Avi1
(7)
式中:Pi1——第i微元段轴向主流方向上游压力;
Pi2——第i微元段轴向主流方向下游压力;
τi——第i微元段流动过程中流体与孔壁的剪切阻力。
对于水平圆管而言,流体与孔壁的剪切阻力τi可表示为:
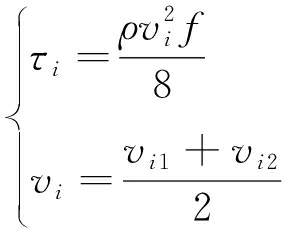
(8)
联立式(7)与(8)可得:
(9)
流量与流速的关系满足:
Q=VA
(10)
联立式(5)、式(6)、式(8)、式(10)可得:
(11)
第i段轴向主流方向上的流量Qi与径向流量qi及下一个微元段主流方向上的流量Qi+1之间的关系为:
Qi-qi=Qi+1, i=1,2…,n
(12)
联立式(4)、式(11)、式(12)即为求解三开裸孔段不同位置处压力的方程组。
由于式(4)为隐式表达式,且第i微元段内压降方程与该段内的径向流量Qi及轴向流量qi有关,因此求解该方程组应采用迭代的方法,其流程如图10所示。
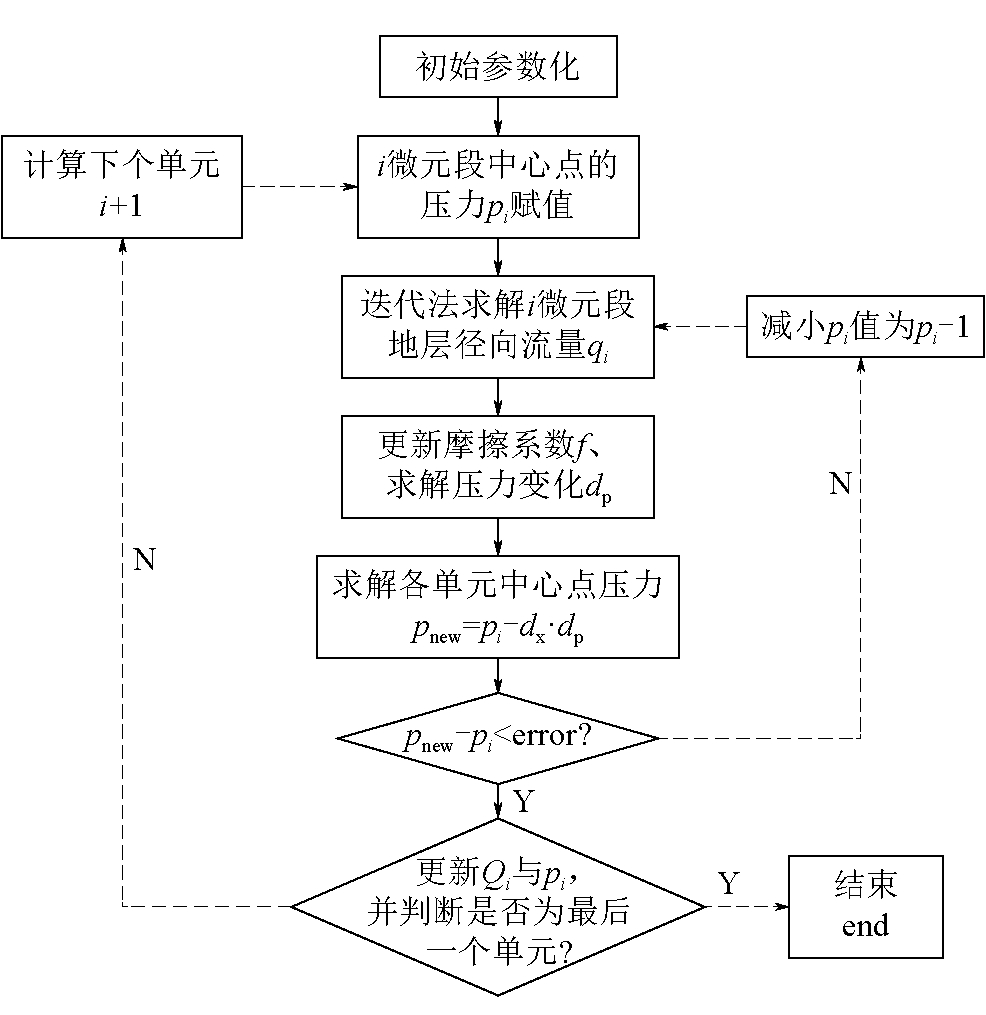
图10 计算流程
迭代法解决该问题的其核心思想为:在先假设第i段对应中心点处压力pi的基础上,求解出对应的径向流量qi,并将其代入第i段压降表达式(11)中,求出对应压降值,同时采用i单元中点压力Pi与Pi1、Pi2的关系,即:Pi-0.5(Pi1-Pi2),来验证所求的pn与假设的pn是否在预设误差范围之内。
以上即为理论研究手段分析顺层裸孔段压力的求解方法,采用相关参数对顺层段压力进行计算分析,经计算可得:p=7.278 MPa;结合图6可知,数值模拟所得顺层段压力p=7.286 MPa。2种研究手段所得压力误差为1.1%,即说明2种研究手段所得结果取得相互印证。
为进一步分析各因素对顺层段压力影响规律,采用数值模拟方法对不同因素影响下各管内的变化规律进行系统分析。
4 影响因素分析
4.1 孔口压力
在保持各管路长度、内径、粗糙度不变的前提下,改变管路1的入口压力大小分别为1.5、2.5、3.5 MPa,研究孔口压力大小对不同管内水压力分布特征的影响规律。不同注入压力下各路径范围内压力随管路长度变化关系如图11所示。

图11 不同注入压力下各路径范围内压力随管路长度变化关系
由图11可知,压力变化存在线性阶段和幂指数变化阶段,变化趋势同之前分析基本一致。当入口压力分别为1.5、2.5、3.5 MPa时,对应出口压力为6.39、7.39、8.39 MPa。入口压力与出口压力的相关性遵循良好的线性关系。这是由于在管路参数不变的情况下,沿程的压力损失不变,所以压力的变化趋势一致,不同注入压力的情况下,压力差值即为入口端压力的差值。
4.2 地层渗透率
在管路3入口压力、长度和地层尺寸等条件保持不变的前提下,等差改变地层内部的渗透率大小,分别为5×10-10、1×10-10、5×10-11、1×10-11、5×10-12 m2,研究地层渗透率对管路3内水压力分布特征的影响规律。不同地层渗透率下管路3压力随管路长度变化如图12所示。
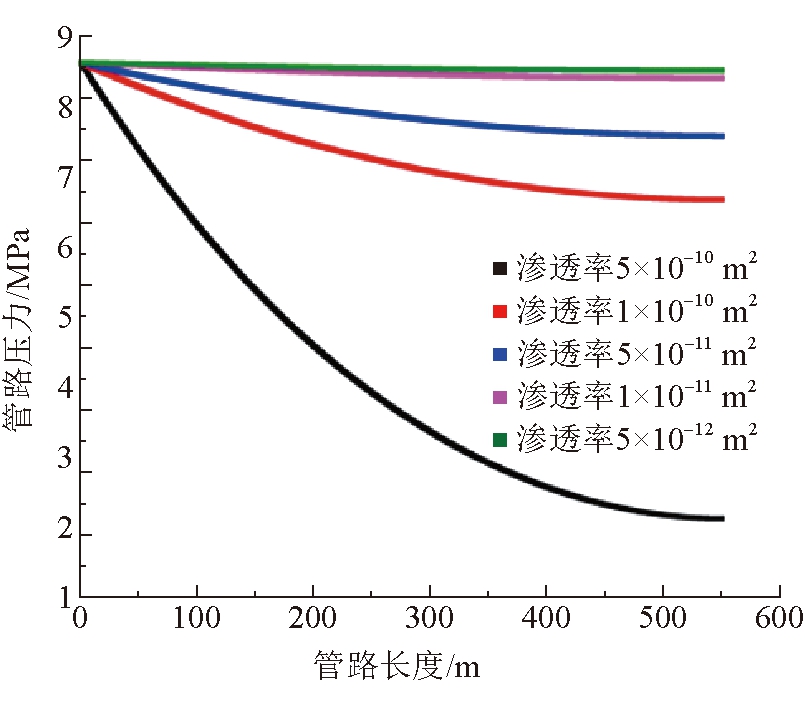
图12 不同地层渗透率下管路3压力随管路长度变化
由图12可知,随着地层渗透率的减小,沿管路3的压力降低逐渐减小。在地层渗透率为5×10-10 m2下,管路3末端压力为5.62 MPa;在地层渗透率为5×10-12 m2下,管路3末端压力为7.37 MPa。可以看出,在地层渗透率较高的情况下,管路3中的压力下降较为明显,随着地层渗透率的减小,压降逐渐减小,当地层渗透率足够低的情况下,管路内流体难以向地层中渗流,可以认为流体主要在管路内流动。
分析其原因,当地层渗透率较大时,管路3内的渗透率与地层渗透率相差较小,流体易从管路内向地层渗流,大量流体渗流到地层中是管路压力下降的主要因素,表现为管路3压力下降较快,末端压力较小;当地层渗透率减小时,流体不易从管路向地层渗透,更多的流体沿着管路3流动,表现为管路3压力下降较慢,末端压力较高;当地层渗透率远小于管路渗透率时,流体不向地层渗流而全部沿管路3流动,表现为压力基本恒定。
4.3 裸孔段管径的影响
在入口压力、地层渗透率等条件保持不变的前提下,改变进入地层后的裸孔段的管径大小(管径分别为0.10、0.15、0.20、0.25 m),研究管路3在不同半径情况下,不同位置处压力分布规律。不同管路半径情况下管路3压力变化如图13所示。
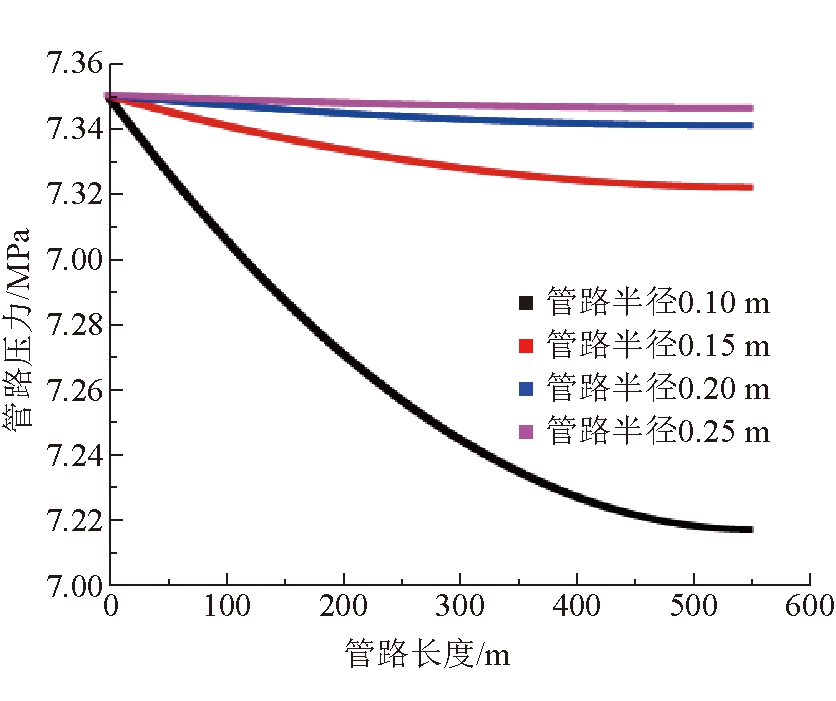
图13 不同管路半径情况下管路3压力变化
由图13可知:当管路3管径分别为0.10、0.15、0.20、0.25 m时,管路3末端压力分别为7.215、7.322、7.345、7.348 MPa,由此可知管路压力随着管径的增大而增加,且当管路管径在0.10~0.20 m区间内变化时,管路压力增长幅度较大;当管路管径在0.20~0.25 m变化时,管路压力基本保持不变,随着管路压力的增大,管路压力趋近于入口压力。
5 结论
(1)通过建立顺层段压水试验的压力求解理论模型,推导得出综合考虑沿程压力损失、局部压力损失及地层渗透扩散等因素影响的不同管路3位置处压力求解理论公式。
(2)建立顺层段各位置压力求解数值分析模型,在数值算例分析与理论算例分析取得相互印证的基础上,综合分析了各因素对压力分布特征的影响规律。
(3)地层裸孔段(管路3)中压力沿管路方向逐渐降低,且下降的幅度逐渐减小,在仅改变注入压力的情况下,管路内的压力分布趋势不变,不同注入压力下管路压力的差值即为入口端压力的差值;地层渗透系数对于裸孔段内压力的影响较大,在高渗透地层中,流体更易从管路中向地层中渗流,管路压力下降快;而对于低渗透地层,流体主要在管路中流动,管路压力下降幅度较小。
[1]陈铭岳.24 m采高条件下工作面底板破坏带发育特征及突水评价[D].徐州:中国矿业大学,2020.
[2]MENG Z P,LI G Q,XIE X T.A geological assessment method of floor water inrush risk and its application[J].Engineering Geology,2012,143-144:51-60.
[3]叶梅.杨庄矿深部采区6煤底板太灰突水危险性评价[D].淮南:安徽理工大学,2017.
[4]曹庆奎,赵斐.基于模糊-支持向量机的煤层底板突水危险性评价[J].煤炭学报,2011,36(4):633-637.
[5]陶真.羊东矿9#煤层底板奥灰突水危险性评价及地下水数值模拟[D].邯郸:河北工程大学,2021.
[6]QIAO W,LI W P,ZHANG X,et al.Prediction of floor water disasters based on fractal analysis of geologic structure and vulnerability index method for deep coal mining in the Yanzhou mining area[J].Geomatics,Natural Hazards and Risk,2019,10(1):1306-1326.
[7]SUI Wanghua,LIU Jinyuan,HU Wei,et al.Experimental investigation on sealing efficiency of chemical grouting in rock fracture with flowing water[J].Tunnelling and Underground Space Technology,2015,50:239-249.
[8]胡洋.煤矿裂隙含水层驱水注浆机制研究[D].徐州:中国矿业大学,2020.
[9]胡洋.承压水上断层活化突水采动效应及其影响因素研究[D].淮南:安徽理工大学,2017.
[10]孙晓宇,田乐,安许良,等.定向钻探注浆技术在煤矿水害防治中的应用[J].建井技术,2019,40(2):17-21.
[11]梁国胜.矿井水害防治中定向钻探注浆技术的应用研究[J].当代化工研究,2020(24):36-37.
[12]李华锋,王庆,冯详.考虑井筒压降的水平井流速及压力分布研究[J].断块油气田,2011,18(3):366-368.
[13]孙恩慧,李晓平.低渗透油藏水平井水平段井筒压力研究[J].油气藏评价与开发,2013,3(2):38-41.
[14]白方方,徐剑明,郑璐璐,等.水平井井控井筒压力分布规律研究[J].重庆科技学院学报,2013,15(4):47-50.
[15]李松泉,廉培庆,李秀生.水平井井筒和气藏耦合的非稳态模型[J].西南石油大学学报,2009,31(1):53-58.
Study on the pressure distribution law of bedding drilling considering the pressure loss in the pipeline and the formation seepage diffusion effect

TONG Shijie,WANG Daokun,HU Yang,et al.Study on the pressure distribution law of bedding drilling considering the pressure loss in the pipeline and the formation seepage diffusion effect[J].China Coal,2023,49(5):63-70.DOI:10.19880/j.cnki.ccm.2023.05.009
- 相关推荐
