大南湖二矿爆破振动影响分析及边坡稳定性研究
时间:2022-02-23 来源:中国煤炭杂志官网 分享:大南湖二矿爆破振动影响分析及边坡稳定性研究
露天矿边坡是采矿形成的人工边坡,部分露天矿 采用爆破作业,而边坡影响区域的爆破振动是边坡失稳破坏的重要外部因素。爆破振动对边坡的影响范围、爆破作用下边坡如何响应以及振动作用下边坡稳定性变化规律,是一系列复杂的工程问题。露天矿生产中单次爆破面积、爆源位置、装药结构、药量大小等变化,产生的爆破振动波强度不同。爆破振动波在不同介质中传递,由于传播介质的波阻抗特性,以及地形、地质条件等因素的不同,其振动强度将会发生改变。因此,输入边坡的爆破振动波强度,爆破对边坡岩体的影响范围,及爆破作用下边坡稳定性变化规律等是边坡安全评价关注内容。
1 大南湖二矿爆破工程简介
大南湖二矿采用延时爆破,矿区爆破振动速度经验公式:
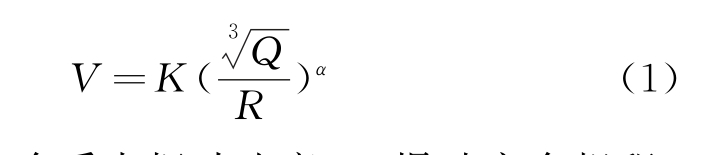
式中:V——安全质点振动速度,《爆破安全规程》对永久性岩石高边坡的安全允许质点振动速度规定其不应超过10.0 cm/s;
K、α——与爆破地点地形、地质条件有关的系数和衰减指数,根据《爆破安全规程》以及现场岩石属于中硬岩石,取K=300,α=2.0;
Q——装药量,t;
R——爆破中心至安全质点的距离,m。
爆破飞石是爆破的主要有害效应,也是爆破警戒距离确定的主要指标,采取合理的前排抵抗线,减小单孔药量,缩小孔排距,增加填塞长度,加强填塞质量是防止浅孔爆破飞石的有效手段。根据伦德伯格(Lundborg)统计规律,R计算如下:
式中:K′——与爆破方式、填塞长度、地质和地形条件有关的系数,取1600~2100;
q——钻孔平均装药量,kg/m3;
D——钻孔直径,mm。
2 现场监测目的与布设方案
在大南湖二矿南帮进行爆破振动监测,通过对监测数据的统计与分析,研究爆破振动对南帮边坡岩体的影响程度。选取典型采掘工作面,采用现场监测数据,模拟爆破振动作用下边坡变化规律,分析爆破振动对南帮边坡的影响程度。振动监测系统由MEMS三向检波器、振动信号采集仪以及软件系统构成。
(1)MEMS三向检波器。测量爆破震源激励下场地的三向加速度振动响应信号。其中,X向表示振动的来波方向(水平切向),Y向表示垂直于来波方向(水平径向),Z向表示竖直向上(垂直方向)。
(2)振动信号采集仪。在矿区南帮布设15个测点,分3组开展爆破振动试验,测点布置区如图1所示。
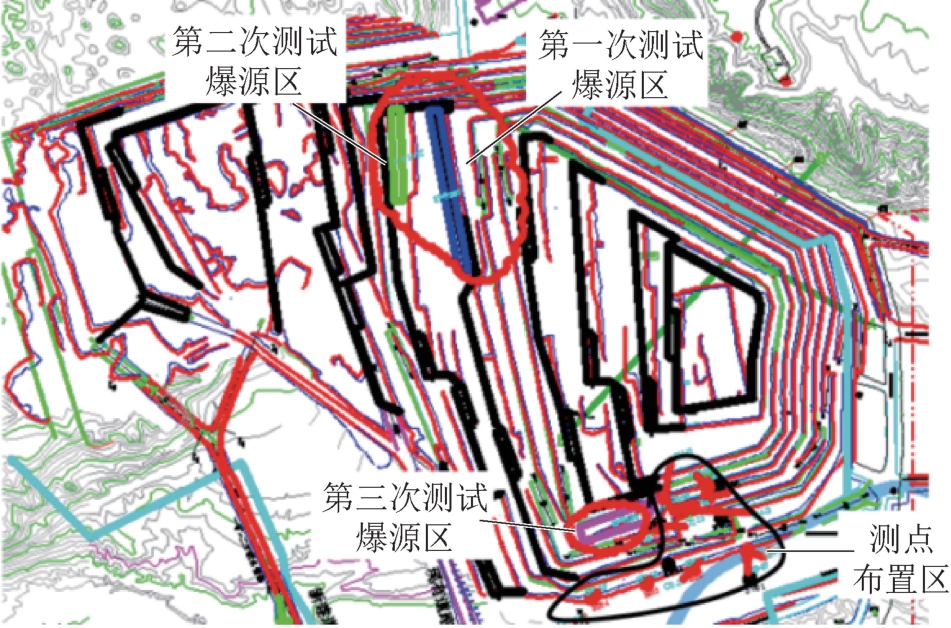
图1 爆破振动爆源点及测点布设图
3 边坡结构爆破振动响应影响研究
3.1 爆破振动分析内容
(1)时域分析。根据震速与时间曲线图,读取测点振动的典型特征数据;研究振动信号的振动幅值等参数、信号的稳态和交变分量随时间的变化情况。通过波形分析得出振动最大值V max,振动最大值对应的时刻t max和振动持续时间t。
(2)振动持续时间分析。指振动波初始到结束的时间,是反应爆破振动强弱的重要指标之一。
(3)主震频率分析。将频谱分析中最大谱值对应的频率称为主频率(又称为卓越频率),爆破分析中常用主频率、主频域来分析不同条件下爆破振动的频谱特征。从频谱图中,得出主频率F max和频率范围F c 2个特征值。
3.2 监测数据分析研究
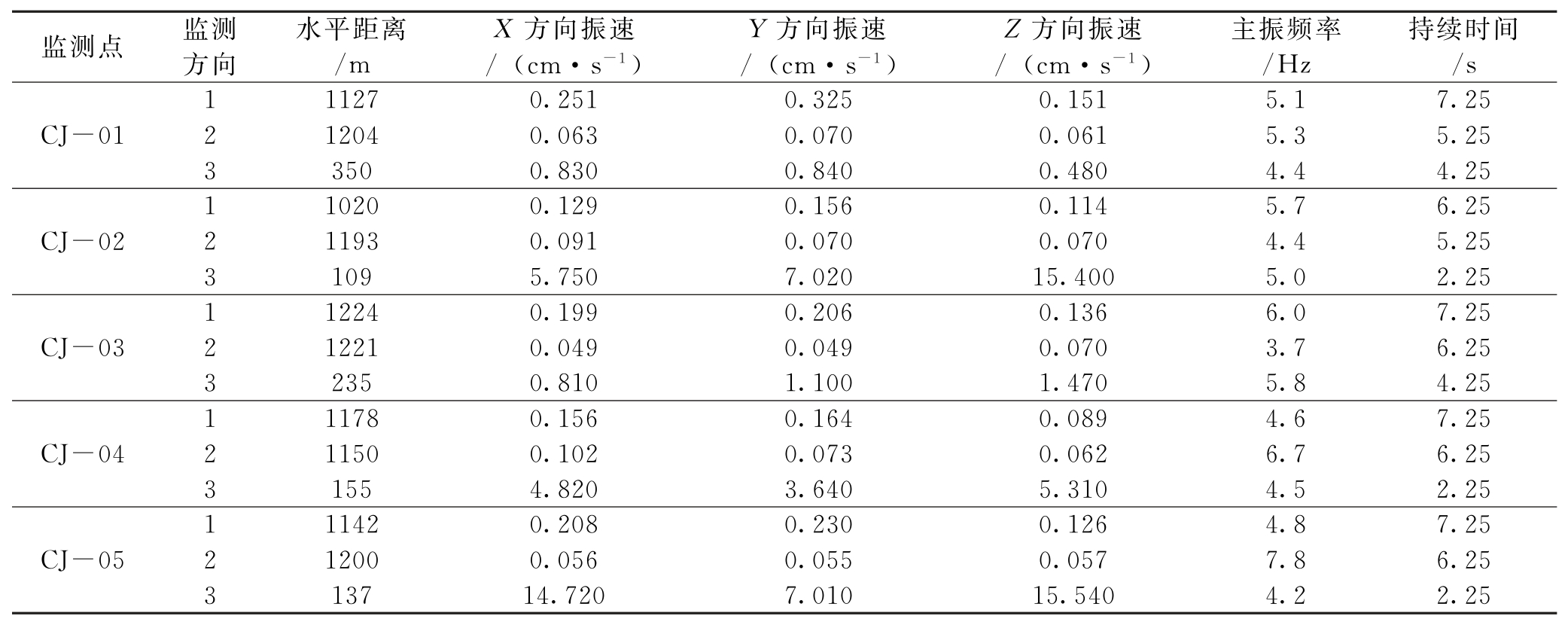
爆破振动效应是边坡结构对爆破振动波载荷激励的动力响应,包括边坡结构受到爆破振动作用而引发内力改变从而引起边坡位移、速度、加速度等变化。本次进行了3组爆破试验,其中每组5个点,利用15组监测数据对边坡响应进行分析,统计数据见表1;选取3组爆破中典型监测曲线,典型监测数据如图2所示。
表1 3组15次监测数据
?

图2 典型监测点X向振动速度波形图
第1组中5个监测点监测到的最大振动速度为0.325 cm/s,最小为0.089 cm/s,在3个方向上,水平方向振动速度大于垂直方向速度;主振频率为4.6~6.0 Hz,振动持续时间约6.25~7.25 s。
第2组中5个监测点监测到的最大振动速度为0.102 cm/s,最小为0.049 cm/s,3个方向上速度较相近;主振频率为3.7~7.8 Hz,振动持续时间约5.25~6.25 s。
第3组爆源位于南帮坡脚区域爆破,南帮振动速度最大为15.54 cm/s,最小为0.48 cm/s,3个方向上垂直方向速度大于水平方向速度;主振频率为4.2~5.8 Hz,振动持续时间约2.25~4.25 s。
通过对15个监测点数据的统计与分析,结果显示距离边坡越近爆破持续时间越短,第3组爆破试验距离南帮近,而振动监测持续时间在2.25~4.25 s;第1组和第2组距离南帮远,而振动监测持续时间在5.25~7.25 s。
在爆破距离相近时,一次爆破区域越大,其振动速度越大。第1组一次总装药量为20 t,第二组总装药量为16.5 t,两组爆源与监测距离相近时,第1组振动速度在0.089~0.325 cm/s,大于第2组的0.049~0.102 cm/s。
在第3组监测数据中,监测点距离爆破区域较近,垂直方向振动速度大于水平方向振动速度;当振动传递至155 m时,3个方向监测数据相近,随距离增大至235 m、350 m,垂直方向速度衰减到1.470 cm/s、0.480 cm/s,且垂直方向振动速度衰减较水平方向衰减快,爆破振动对边坡影响主要是水平方向振动波影响。
选取监测点距离爆破中心X为137 m、155 m、235 m、350 m、1150 m、1200 m,水平方向速度V最大值分别为:14.720 cm/s、4.820 cm/s、1.100 cm/s、0.830 cm/s、0.102 cm/s、0.056 cm/s,模拟爆破中心振动波水平方向衰减规律,数据拟合资料见图3所示,其衰减规律为:
当距离达到350 m时监测点数据小于1 cm/s,因此爆破振动影响距离小于为350 m。
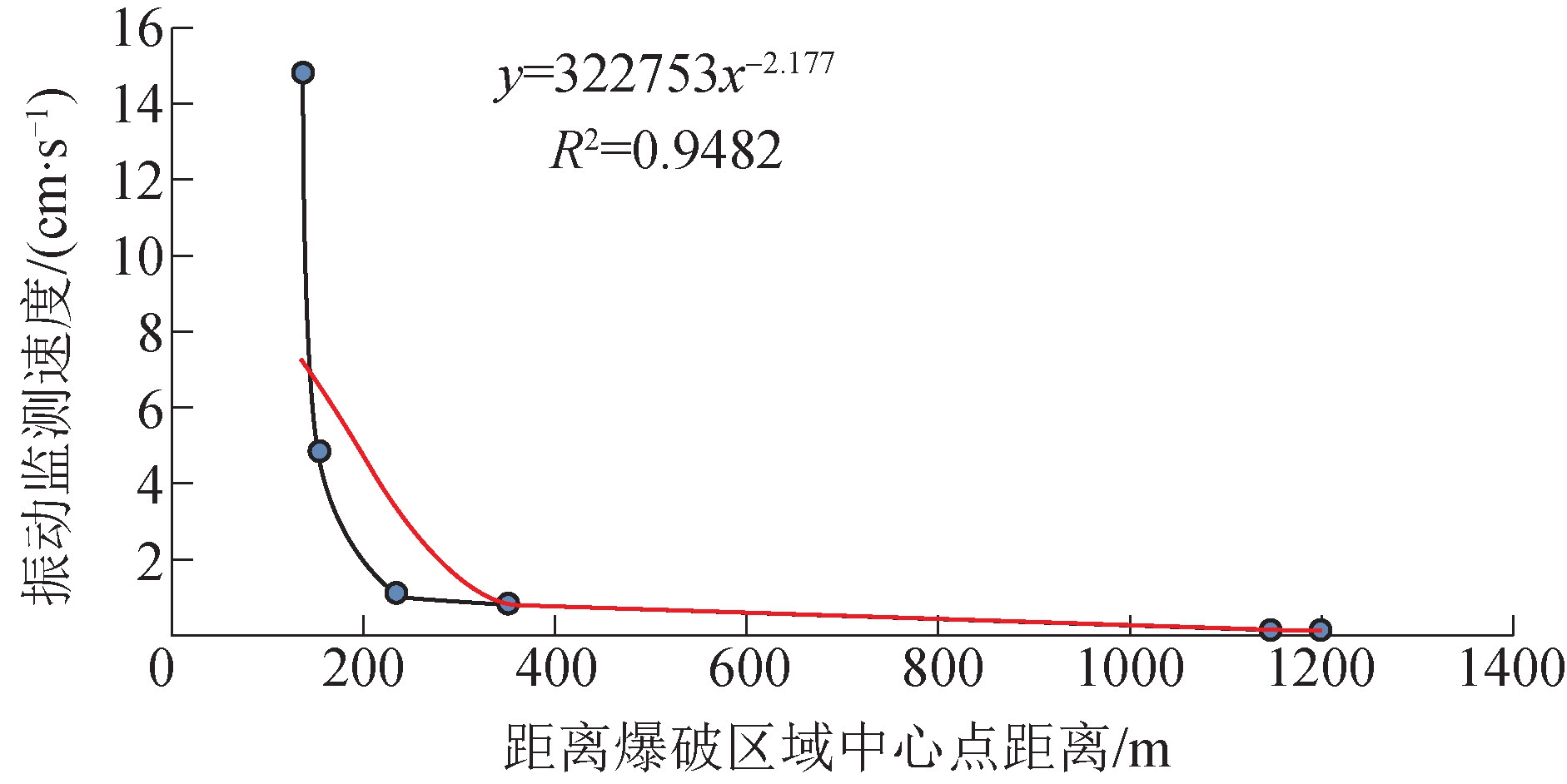
图3 爆破振动速度衰减规律研究
4 爆破振动对边坡影响及边坡安全评价
爆破振动效应会引起岩体不同程度的损伤甚至破坏,当爆破振动达到一定程度时,会造成露天矿边坡失稳,严重时可能引起地质灾害和整体坍塌。通过对已有爆破振动资料整理和分析,选取图2中第3组南帮坡脚爆破振动波,输入模型后振动波持续影响时间为0.9~1.9 s。研究爆破对南帮剖面-3边坡岩体的影响,模型图见图4,并分析爆破波对边坡稳定性的影响。
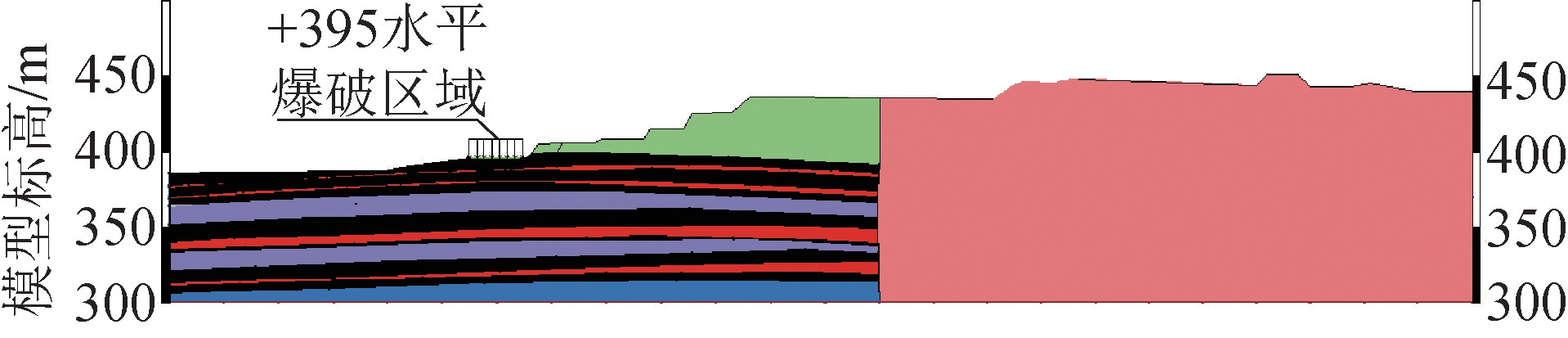
图4 爆破振动数值计算中布设监测点位置
4.1 南帮岩体爆破振动影响程度研究
4.1.1 南帮岩体动剪应力峰值动力(q)响应规律
在+395 m水平爆破振动作用下,边坡岩体在动剪应力作用下,初始阶段0.7163 s时,在爆破区域下方岩体中形成剪切破坏区域,如图5(a)所示。随振动加载时间累积,爆破影响规律显现明显。在振动持续时间达到1.9913 s时,爆破振动影响程度达到最深,在爆破区域,边坡岩体水平方向上影响达到152.50 m,影响至+405 m水平台阶,同时CJ05监测组第3个监测点位于该区域,且监测数据速度较大竖直方向深度影响至25.04 m,如图5(b)所示。
4.1.2 南帮岩体水平方向位移变化规律
在+395水平爆破振动作用下,边坡岩体水平方向位移规律,初始爆破区域变形由浅层向两侧扩展过程,如图6所示;随振动波的增大与振动持续时间的加长,在爆破区域下部表现为向浅层及深部岩体两侧的水平位移,图6(b)中表现明显。

图5 爆破作用下边坡岩体剪应力响应

图6 爆破作用下边坡岩体水平方向位移变形
4.1.3 南帮岩体竖直方向位移变化规律
在+395 m水平爆破振动作用下,边坡岩体垂直方向位移影响随爆破振动增强和振动持续时间的延长,影响范围逐渐增大,如图7所示。在振动持续时间达到1.9913 s时,水平方向上影响爆破区域达173.10 m,垂直方向上向深部影响74.81 m,见图7(b)所示。

图7 爆破作用下边坡岩体垂直方向位移变形图
4.2 爆破振动作用下南帮边坡稳定性变化规律
在南帮岩体爆破振动影响研究的基础上,研究振动作用下边坡稳定性变化规律,通过极限平衡计算得出,南帮边坡初始状态时边坡稳定性为2.38。在爆破振动期间,爆破振动波持续时间主要集中在1.6~1.8 s之间,随振动时间的持续,边坡稳定性出现波动变化,如图8所示;边坡稳定性变化规律与振动规律一致时,其稳定性逐渐降低,最低时为1.033,如图9所示。因此,爆破作用下边坡出现瞬时稳定性降低现象,大于临滑状态稳定系数1.0,坡脚爆破时边坡处于安全状态。
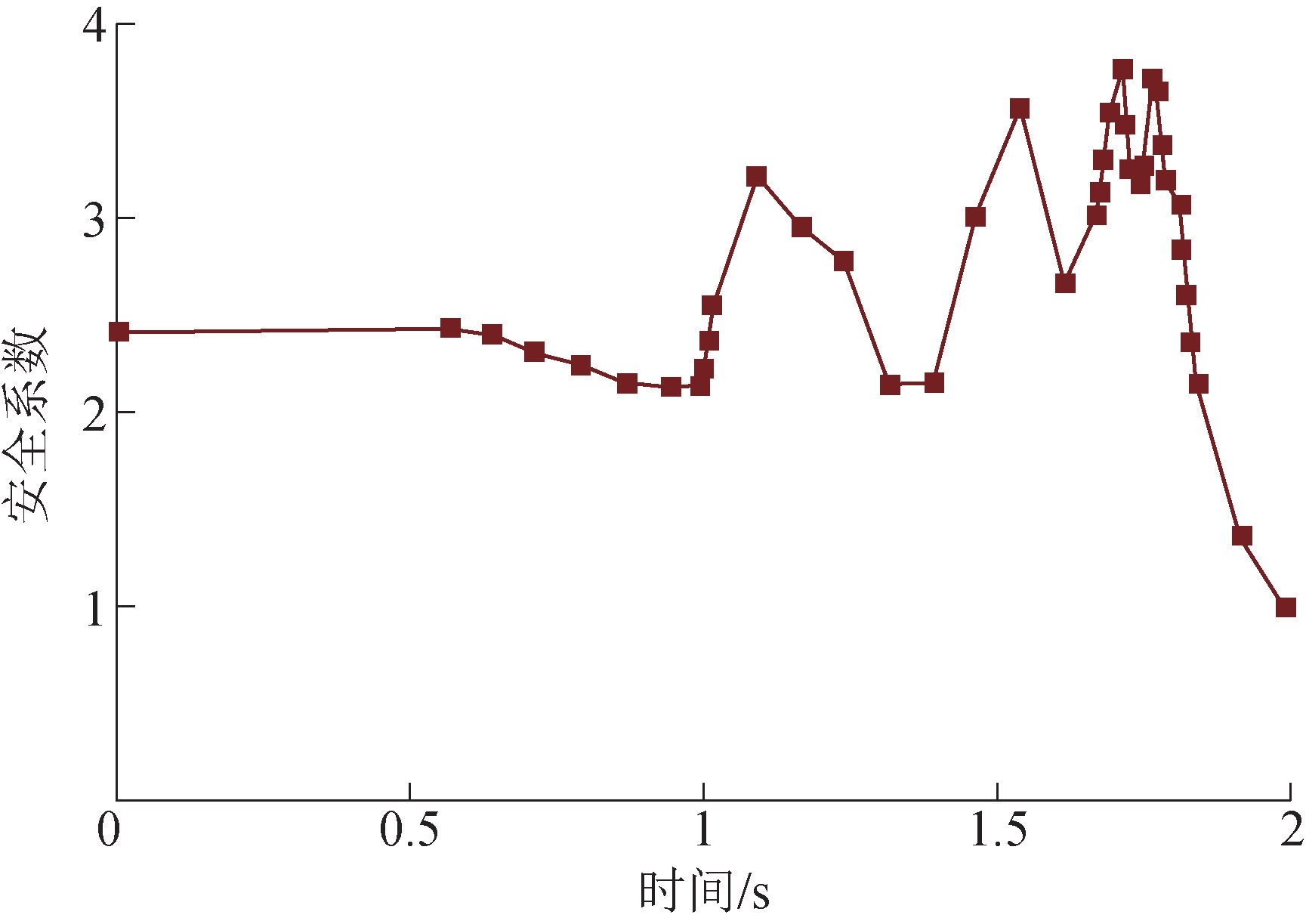
图8 爆破作用下南帮稳定性变化图
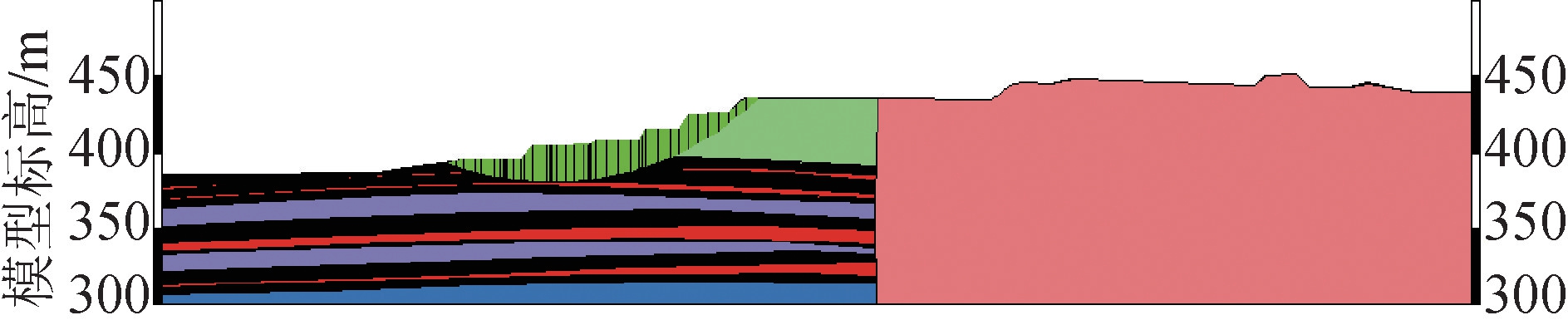
图9 爆破作用下南帮边坡出现的最低稳定性
5 结论
(1)监测大南湖二矿矿区爆破对南帮岩体的影响,通过对监测点数据统计分析,距离边坡越近,爆破对南帮作用持续的时间越短;在爆破区域距离相近时,装药量越大,其振动速度越大;监测点距离爆破区域越近时,垂直方向振动速度大于水平方向振动速度;随振动传递距离增加,垂直方向速度衰减程度大于水平方向速度衰减;水平方向爆破振动衰减与距离呈幂函数关系,衰减公式为V=322753X-2.177,在爆破振动距离在350 m以内时,南帮边坡振动速度影响较大。
(2)在+395 m水平爆破振动作用下,在0.9 s开始有爆破振动影响,至1.9 s影响停止,在此期间选取应力和位移作为岩体变形破坏依据。根据应力和位移变化,边坡岩体在爆破振动初始阶段变形主要在爆破区域浅层岩石;随振动持续影响,变形逐渐向深部及西侧岩体扩张。主要影响至边坡+405 m水平,在动剪应力作用下,水平方向上影响爆破区域两侧至152.50 m,深度影响至25.04 m;而推动变形影响中,水平方向影响爆破区域173.10 m,垂直方向上向深部影响74.81 m。因此,爆破振动在岩体中水平方向的影响在152.5~173.10 m之间,而深部影响达到25~74.81 m。
(3)结合矿区爆破振动监测,模拟研究了爆破振动作用下南帮边坡稳定性变化规律,在振动影响下边坡稳定性降低;爆破振动波集中在1.6~1.8 s之间,剖面的稳定性随振动波的幅度而变化,稳定性变化规律与振动时间曲线可以相互吻合,随振动结束边坡稳定性恢复,最大振动波时其稳定性最低为1.033;因此,爆破作用下边坡出现瞬时稳定性降低现象,但可以满足边坡稳定性大于临滑状态稳定系数1.0的安全要求。
[1] 费志超,袁绍国,郭鲁川,等.露天矿控制爆破测震与数据分析[J].现代矿业,2013,29(7):90-91,97.
[2] 刘玉福,王振伟.哈尔乌素露天煤矿边坡爆破振动安全评价与数据分析[J].煤矿安全,2014,45(6):215-217,221.
[3] 王和平.露天煤矿爆破振动对非工作帮边坡稳定性的影响研究[J].能源与环保,2017,39(7):115-121.
[4] 高文学,刘宏宇,刘洪洋,等.爆破开挖对路堑高边坡稳定性影响分析[J].岩石力学与工程学报,2010,29(5):2982-2987.
[5] 李翔龙,庙延钢,杨溢,等.爆破振动对边坡稳定性影响分析[J].爆破,2006,23(4).15-19,29.
[6] 万江涛,田睿,王滨,等.爆破振动对高陡边坡稳定性影响分析[J].西部探矿工程,2012(4):1-3.
[7] 张建华,黄刚.爆破震动对HML露天矿边坡影响的研究[J].爆破,2012,29(6).114-118.
[8] 王志亮,李其中,张莉聪.煤层预裂爆破应力波破坏范围的探讨[J].中国煤炭,2010,36(3):52-55.
[9] 许红涛,卢文波,周创兵,等.基于时程分析的岩质高边坡开挖爆破动力稳定性计算方法[J].岩石力学与工程学报,2006,25(11):2213-2219.
[10] 郭振春.浅谈露天矿邻近最终边坡的爆破技术和减震措施[J].现代矿业,2011,27(1):97-98.
Influence analysis of blasting vibration and study on slope stability in Dananhu No.2 Mine
Zhao Jinsheng,Yan Jie,Li Chao,et al.Influence analysis of blasting vibration and study on slope stability in Dananhu No.2 Mine[J].China Coal,2020,46(8):102-107.doi:10.19880/j.cnki.ccm.2020.09.016
- 相关推荐

