采空区积水条件下工作面推进速度对煤岩层稳定性影响研究
时间:2023-10-30 来源:中国煤炭杂志官网 分享:★ 煤矿安全 ★
采空区积水条件下工作面推进速度对煤岩层稳定性影响研究
0 引言
矿井水害已成为煤矿事故中仅次于瓦斯的第二大灾害,而采空区突水占煤矿水害事故的比重非常大。采空区突水具有时间短、水量大、破坏性强等特点[1-4]。
我国煤矿开采历史悠久,由于早期开采方法与技术落后,一些小煤矿为了开采便利,采用巷道式、房柱式采煤方法对下煤层随意进行采掘,产生了大量错综复杂的采空区[5-6]。采空区形成后,岩层的自然应力状态和平衡状态受到破坏,岩层内部的应力需要重新分布以达到新的平衡状态,这导致采空区上覆岩层变形、垮落、断裂、离层和移动,形成裂缝带。严重时,岩层的裂隙可能贯通含水层,导致水沙溃入工作面,损坏工作面和井下设备,造成人员伤亡[7]。
因此,采空区积水是威胁矿井安全生产的因素之一,研究采空区积水条件下工作面推进速度对煤岩层稳定性的影响规律,对矿井的安全生产具有重要意义。笔者以黑龙江龙煤七台河矿业有限责任公司龙湖煤矿(以下简称“龙湖煤矿”)积水勘测项目为工程背景,通过瞬变电磁法对该矿区北-东一采区及南二采区进行探测,分析采空区积水异常区分布情况。
1 煤层概况
选取龙湖煤矿63、64号煤层作为研究对象,通过理论分析、室内力学实验、数值模拟等研究方法,分析了在采空区积水条件下,工作面推进速度对煤岩层稳定性的影响规律。63号煤层为已开挖煤层,煤层平均厚度1.4 m,存在大面积采空区积水;64号煤层正在施工开采,位于63号煤层下方,煤层平均厚度1.8 m。龙湖煤矿煤种为焦煤,煤层结构简单,煤层厚度变化不大,较稳定。64号煤层顶板为粉砂岩、中砂岩,底板为粉砂岩,质地较坚硬,裂隙不发育,对工作面无影响。研究区域地面平均标高+310 m,64号煤层工作面标高-350 m,可采走向长度538 m,倾斜长度200 m,倾角5°。研究区段煤岩层柱状如图1所示。

图1 研究区段煤岩层柱状
2 数值模型的建立
2.1 煤岩体力学参数测定
结合图1煤层柱状图,对相应的代表区域进行现场取样。在实验室制作岩石试样后通过室内力学实验,最终获取各煤岩层物理力学参数,见表1。
表1 现场取样物理力学参数实验结果
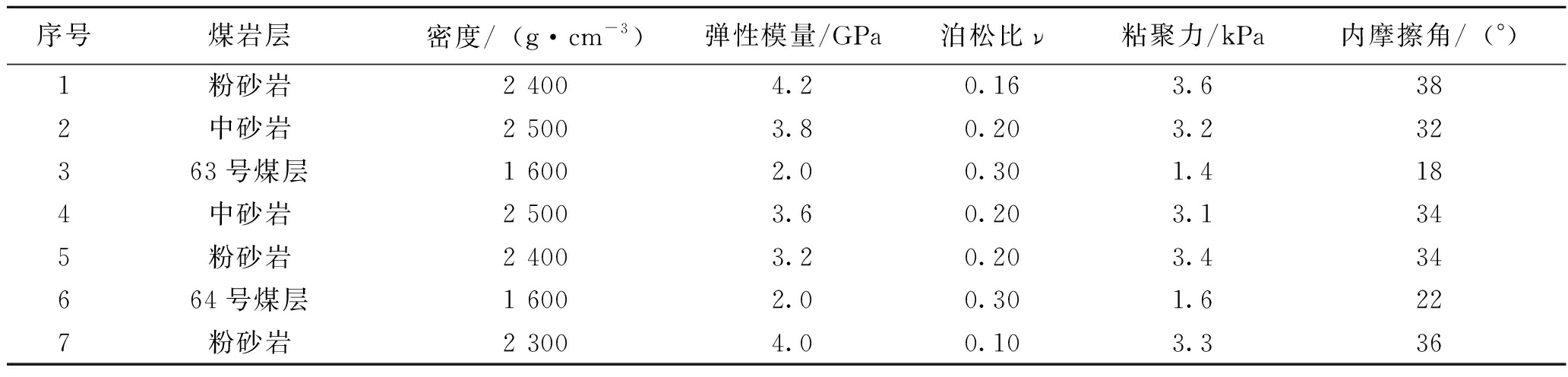
序号煤岩层密度/(g·cm-3)弹性模量/GPa泊松比ν粘聚力/kPa内摩擦角/(°)1粉砂岩2 4004.20.163.6382中砂岩2 5003.80.203.232363号煤层1 6002.00.301.4184中砂岩2 5003.60.203.1345粉砂岩2 4003.20.203.434664号煤层1 6002.00.301.6227粉砂岩2 3004.00.103.336
2.2 煤岩层流固耦合及弹塑性力学理论
2.2.1 渗流-应力耦合理论
(1)基本理论。流固耦合理论在地下工程中是研究流体与岩体相互作用的一种重要理论依据。岩体固体在渗流场的作用下会产生相应的位移及变形,同时位移与变形也会影响渗流场[8]。
当应力为拉应力且孔隙压力达到饱和状态时,岩体有效应力是正值。其表达式为:
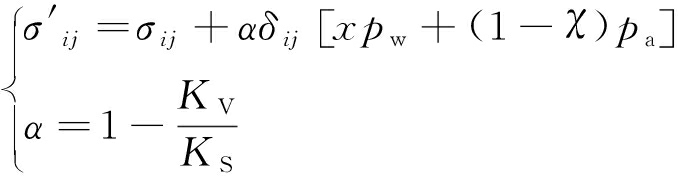
(1)
式中:![]() 有效应力;
有效应力;
σij——总应力;
x——与饱和度以及表面张力相关参数;
pw——孔隙水压力;
pa——孔隙气压力;
δij——Kronecker符号;
α——Biot系数,一般取1;
KV——岩石体积的压缩模量;
KS——固体颗粒的压缩模量。
(2)平衡方程。在地层结构中,岩土体应力平衡方程可以通过虚功原理描述,也就是说,在特定的时间点,岩土体受到体力和面力的影响,会导致它们之间的虚功保持不变,即:
(2)
式中:t——面力;
f——体力;
V——岩石体积;
S——固体颗粒;
T——特定时间点;
σ——应变;
δε——虚应变;
δu——虚位移。
2.2.2 弹塑性力学理论
在地下工程中,煤岩层的承载受力通常分为弹性阶段、塑性阶段和损伤破坏阶段,其应力应变演化规律具有明显的非线性特征。当岩石受地层活动影响所受到的应力值低于极限状态时,应力-应变曲线服从胡克定律,为弹性变化阶段;随着应力的持续增大,超过岩石的弹性极限时,它的应力-应变变化不再按照原来的胡克模式发生,这时进入塑性变化阶段。在材料开始屈服以后,煤岩层因受到周边未屈服物质的阻挡而保持稳定,不会立刻崩溃。根据流体力学原理,在这个阶段,材料的应力-应变关系可以用应变增量来描述,其中,弹性应变增量反映了煤岩石材料的可恢复变形能力,而塑性应变增量反映了岩石的损伤和破坏程度。通常,理想的弹性塑料的初始屈服点与破坏点的应力相同,但应变却有所差异。软硬岩土在初始屈服后,会经历塑性阶段,最终形成破坏面。典型岩土应力-应变演化规律[9]如图2所示。
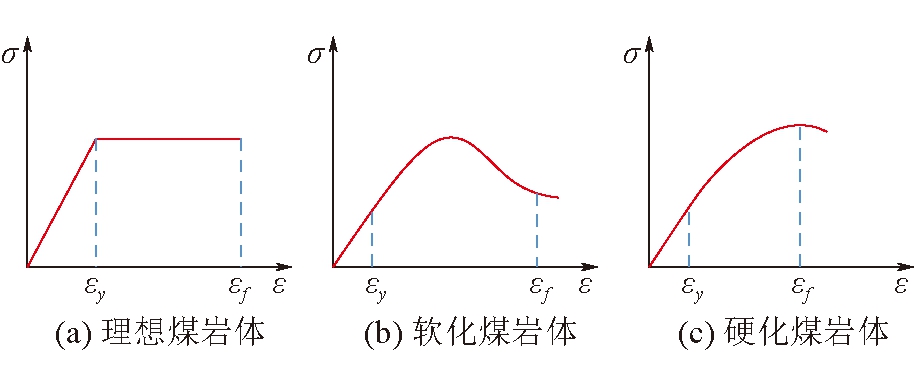
图2 煤岩体典型应力-应变曲线
2.3 模型建立
数值计算参数参照龙湖煤矿63号、64号煤层。模型尺寸选定沿煤层走向长度160 m,沿工作面倾斜长度300 m,模型高度80 m,即整体模型尺寸为300 m×160 m×80 m(长×宽×高)。根据积水勘测项目探测结果设定63号煤层为已开挖采空区积水煤层,煤层厚度1.4 m,煤层倾角5°,采空区走向长度36 m,中部24 m为积水异常区;未开挖64号煤层厚度1.8 m,煤层倾角5°,工作面倾斜长度200 m,沿煤层走向分步开挖,最终挖掘长度60 m。为模拟上覆岩层重量,将其重量转化为14 MPa等效均布荷载作用于模型顶部。各岩层属性及深度参照图1的煤层柱状,将煤层及各类型岩层分区,得到数值模型网格划分如图3所示。
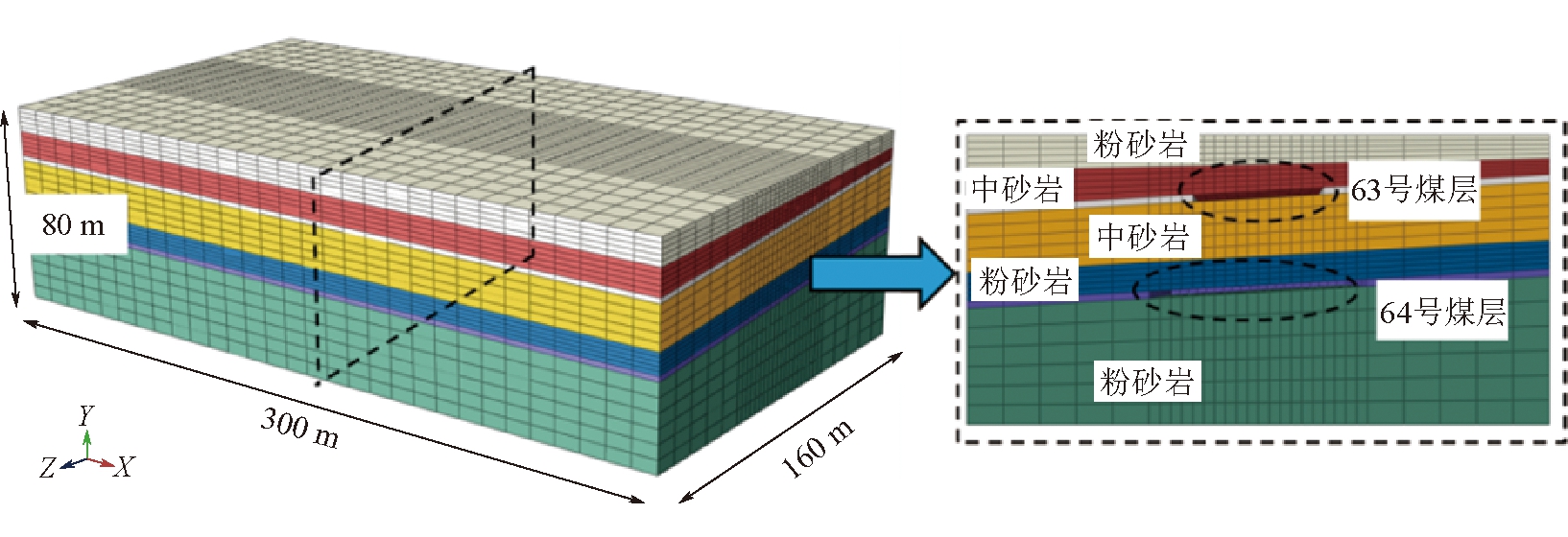
图3 数值模拟网格划分
以工作面推进速度2 m/d工况模型为例,考虑到采空区积水效应的影响,网格单元设定为ABAQUS用于计算地下孔隙流体应力的八节点六面体单元(C3D8P),模型共划分单元22 800个,节点数量25 420个。对于模型位移边界条件,限制左右两侧X方向的水平位移,模型前后Z方向的位移,以及模型底部Y方向的水平位移。此外,由于上部煤层存在24 m积水异常区,通过在该区域施加0.8 MPa的孔隙水压力荷载来实现积水异常的不利荷载影响。该模型采用弹塑性本构模型,结构服从莫尔-库仑(Mohr-Coulomb)准则。
3 模拟方案及数值模拟结果
在上部煤层采空区积水影响下,为探究下部煤层开采时工作面不同推进速度对层间煤柱的扰动影响,根据不同的推进速度逐次开挖,模拟工作面推进60 m时煤柱破坏变形规律特征。分别选取工作面推进速度2、4、6 m/d的3种工况展开分析,在数值模拟的静力学分析中,为保证不同的工作面推进速度应用于数值模拟不同工况之中,故模拟将工作面推进速度等效成开挖步距来表示。为减小边界条件效应,模型沿开挖走向两端各留设50 m煤柱,沿倾向各留设100 m煤柱。
分析工作面以2、4、6 m/d的速度推进工况下,其位移分布、水压力状态、应力特征以及煤层周边破坏演化规律,为便于后续对比分析,每组工况分别选取工作面推进距离0、12、24、36、48、60 m条件时的数据云图展开讨论与分析。
3.1 不同工况下煤岩层应力变化
为了研究不同工况开挖后煤岩层的应力变化,模拟计算不同的开采工况,鉴于篇幅限制,以工作面推进2 m/d工况为例进行分析。
工作面推进速度2 m/d工况下不同推进距离条件下煤岩层应力分布如图4所示。由图4可以看出,在采空区影响及承压水压共同作用下,煤层开采后煤岩体的原始应力场遭受破坏,工作面附近应力集中,并随工作面逐步推进,工作面应力集中现象越显著,最终工作面推进60 m时,应力峰值达到最大。推进速度越快,应力峰值也越大。
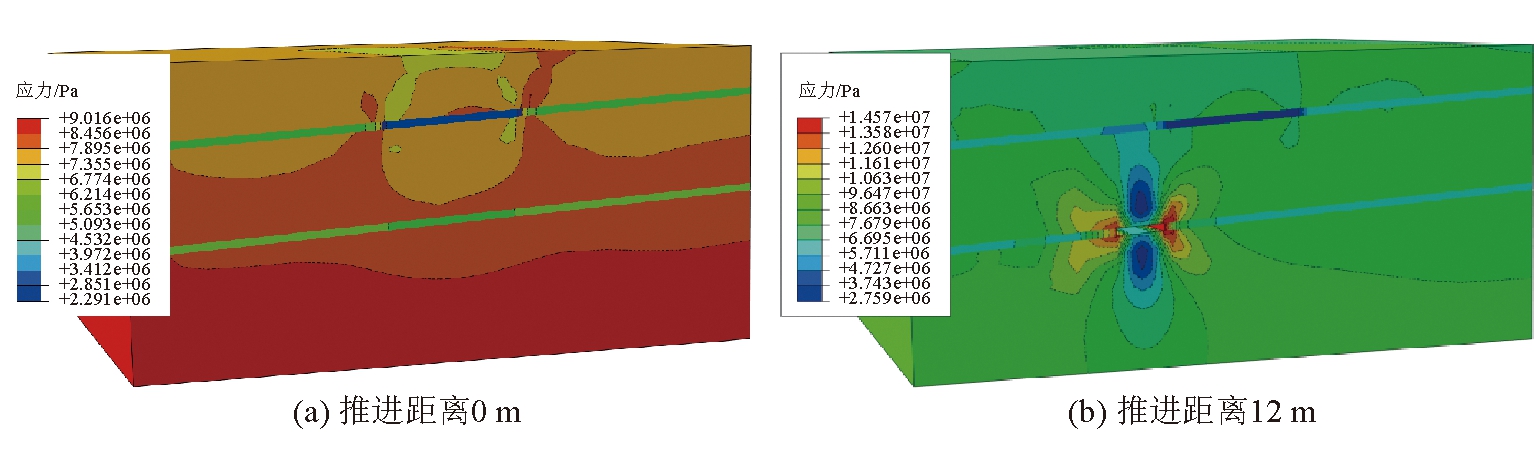
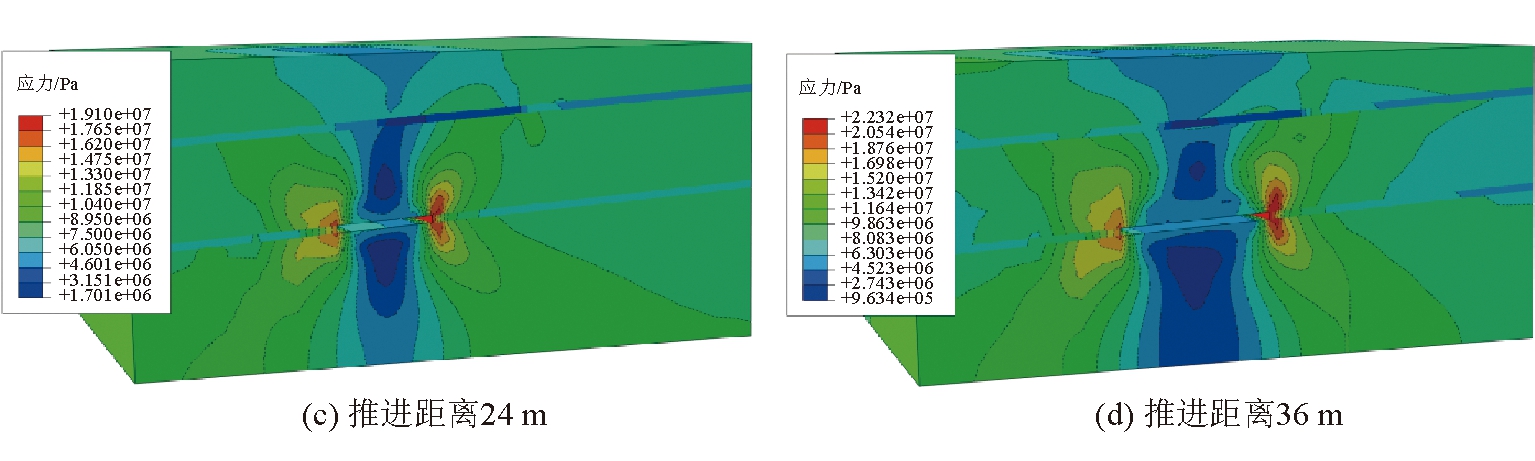
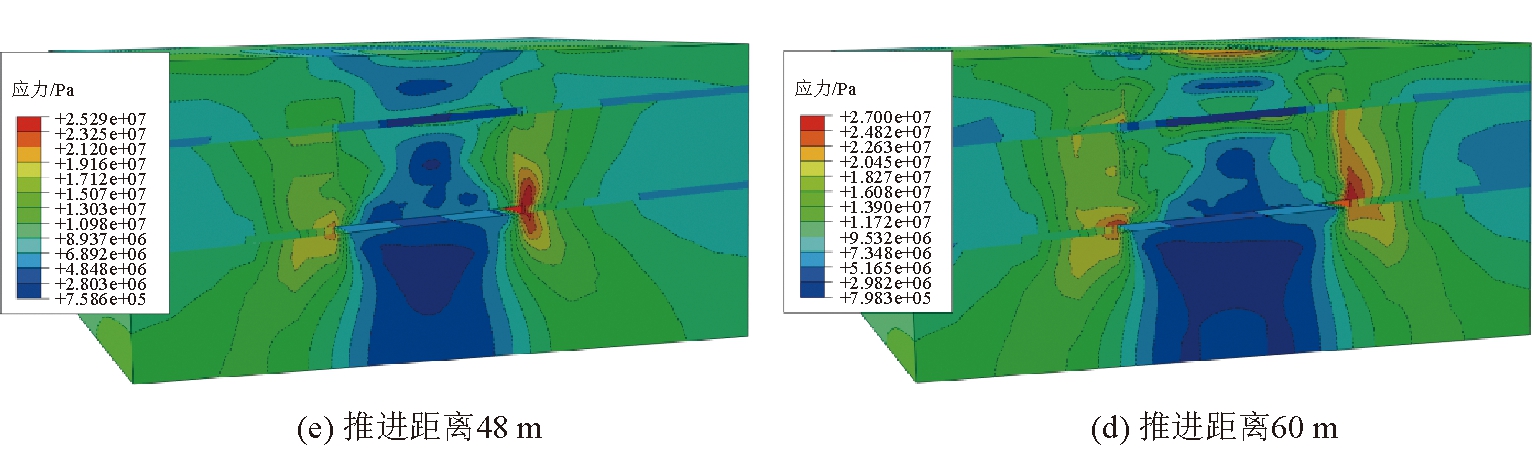
图4 工作面推进2 m/d时的煤岩层应力分布情况
3.2 不同工况下煤岩层位移变化
工作面推进2 m/d工况下不同推进距离条件下煤岩层位移分布如图5所示。由图5可以看出,在上覆采空区积水影响下,随着煤层开采,工作面推进过程中煤岩层的位移沉降规律经历了积水影响异常区、工作面沉降影响区以及上下煤层沉降贯通区3个阶段过程。推进速度越快,煤层位移沉降量就越大。

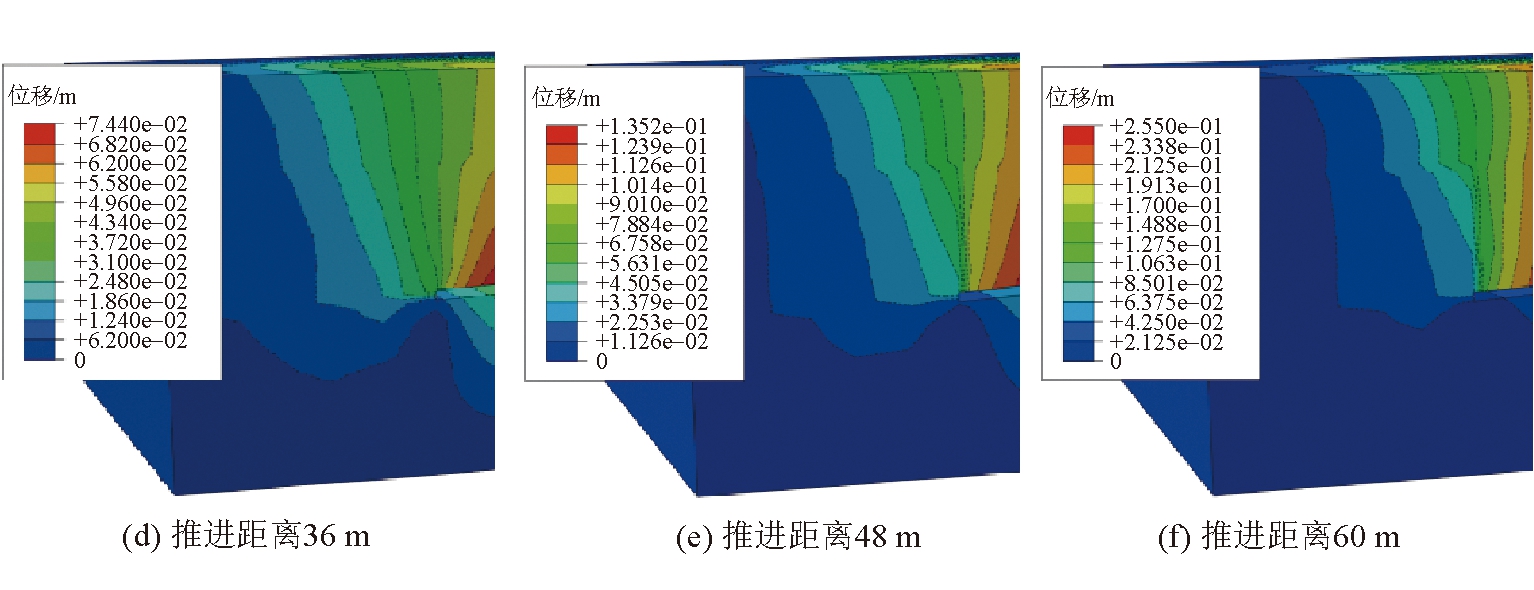
图5 工作面推进2 m/d时的煤岩层位移分布情况
3.3 不同工况下煤岩层水压力变化
工作面推进2 m/d工况下不同推进距离条件下煤岩层水压力分布如图6所示。由图6可以看出,随着工作面的推进,由上部煤层积水区产生的水流经过岩层裂隙涌入下部开采区,增加下部煤层突涌水的风险。对于工作面不同推进速度工况条件下,水压力随推进速度的增加而略有增大。
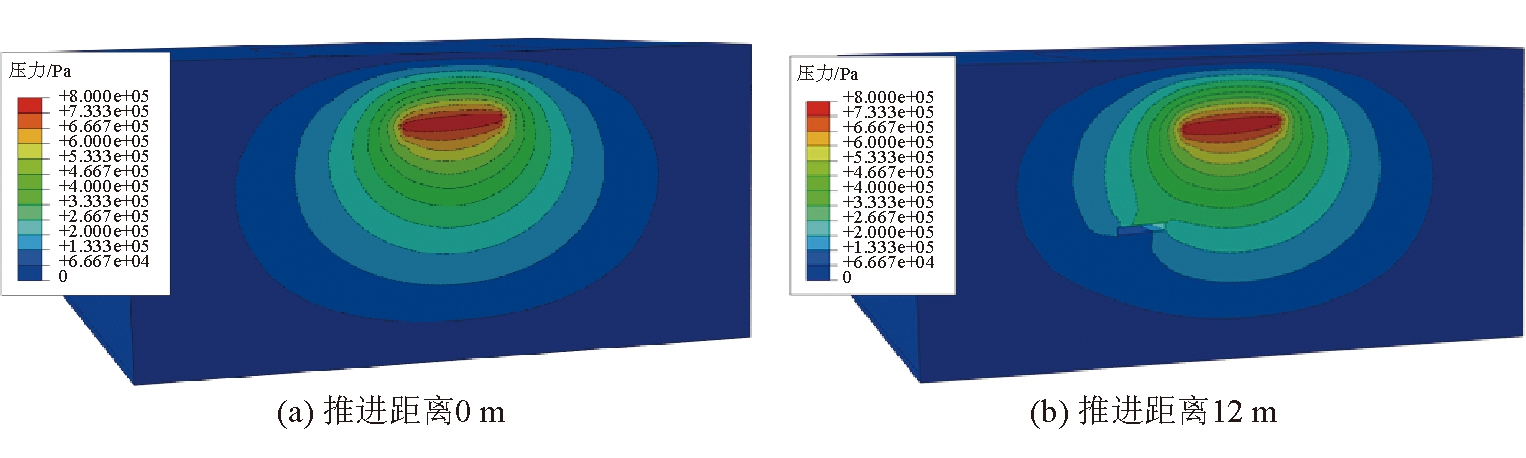
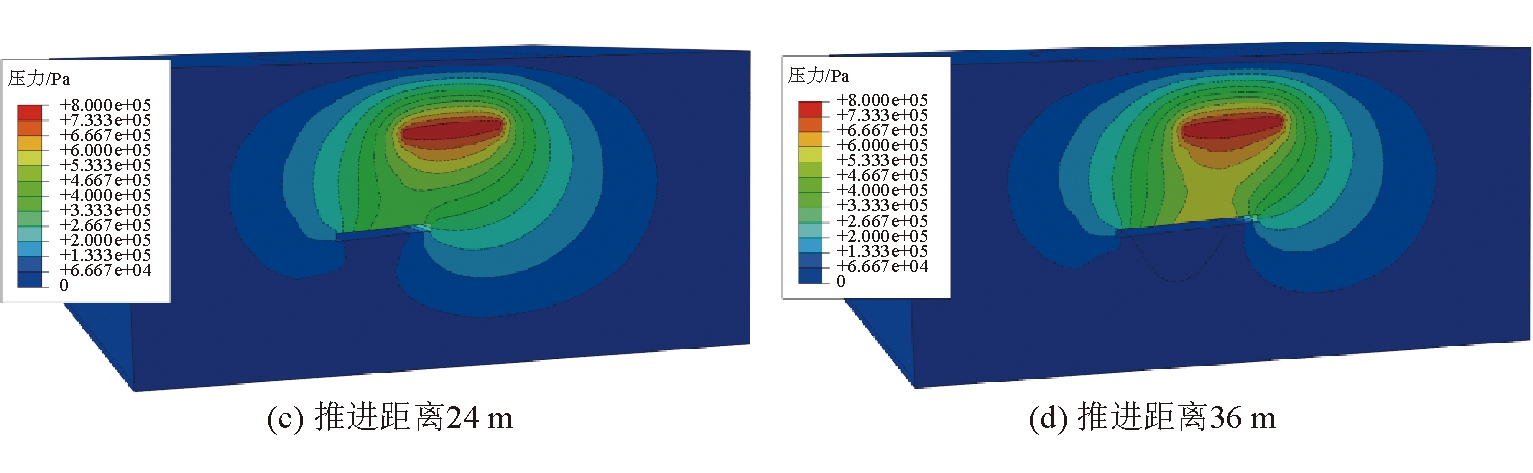
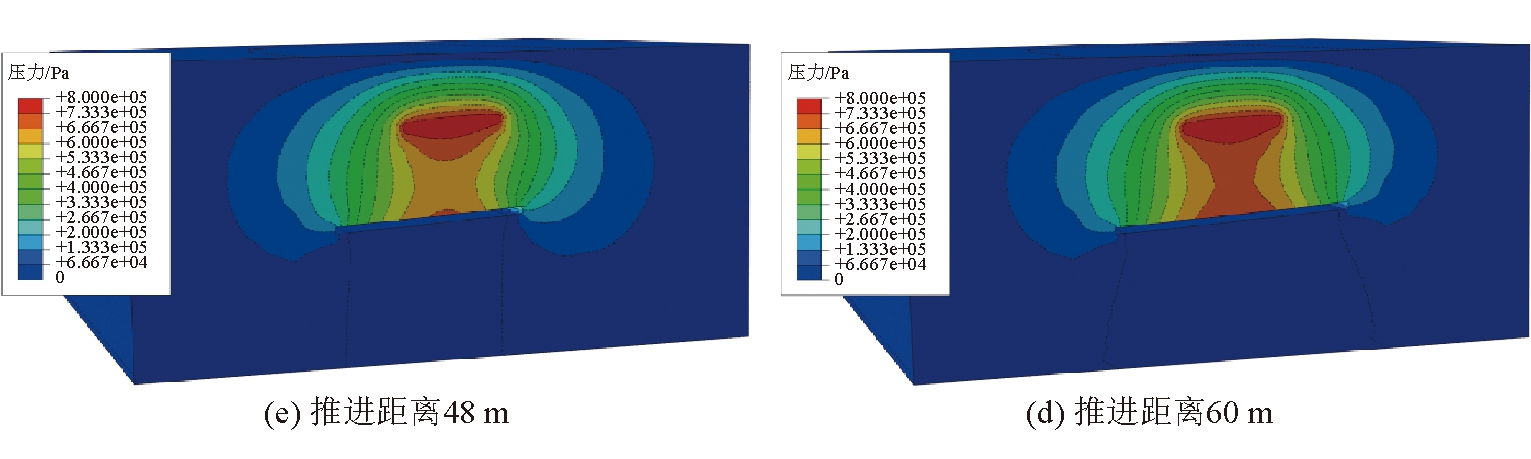
图6 工作面推进2 m/d时的煤岩层水压力分布情况
3.4 不同工况下煤岩层岩层塑性应变
工作面推进2 m/d工况时不同推进距离条件下煤岩层塑性应变分布如图7所示。由图7可以看出,塑性应变是反映地层由弹性阶段过渡至塑性损伤破坏的一个重要指标。在工作面推进初期,推进距离小于36 m,由于煤层工作面远离上覆煤层积水异常区,因此仅工作面附近煤岩层产生扰动,存在塑性变形。当下覆煤层继续开采逐步靠近积水区时(推进36 m),受积水异常区及下部采空区开采扰动的双重影响,其上覆煤层同样出现了塑性区。最终,工作面推进至60 m后,上下煤层塑性区形成贯通,最大塑性应变值达到了0.021 5。



图7 工作面推进2 m/d时的煤岩层塑性应变分布情况
3.5 不同工况下层间岩层稳定性分析
为分析整个煤层开采过程对煤岩层结构稳定性的影响,故选取距离初始工作面36 m时煤层顶部特征点作为典型监测点,分析工作面不同的推进速度对煤层开采过程的应力、位移、水压力以及塑性应变的演化规律。测点位置如图8所示。

图8 测点位置
开采过程监测点应力变化曲线如图9所示。由图9可以看出,在煤层开采过程中,测点应力在3种工况条件下均呈现出先上升后下降的规律,当推进距离小于36 m时,工作面与监测点的距离逐步靠近,受到的煤岩层扰动产生的应力不断积聚,当工作面达到监测点所在截面时(开采36 m),应力集中现象最为显著。工作面继续向前推进后,由于监测点两侧均为邻空面,产生应力释放,应力值急剧减小,最后趋于稳定。同时,可以看出不同工作面推进距离工况下,应力峰值大小也存在差异,呈现出推进速度越快,应力峰值越大的规律。当工作面推进距离36 m时,工作面推进速度为2、4、6 m/d时应力峰值分别为32.9、26.3、21.7 MPa,差异性明显。
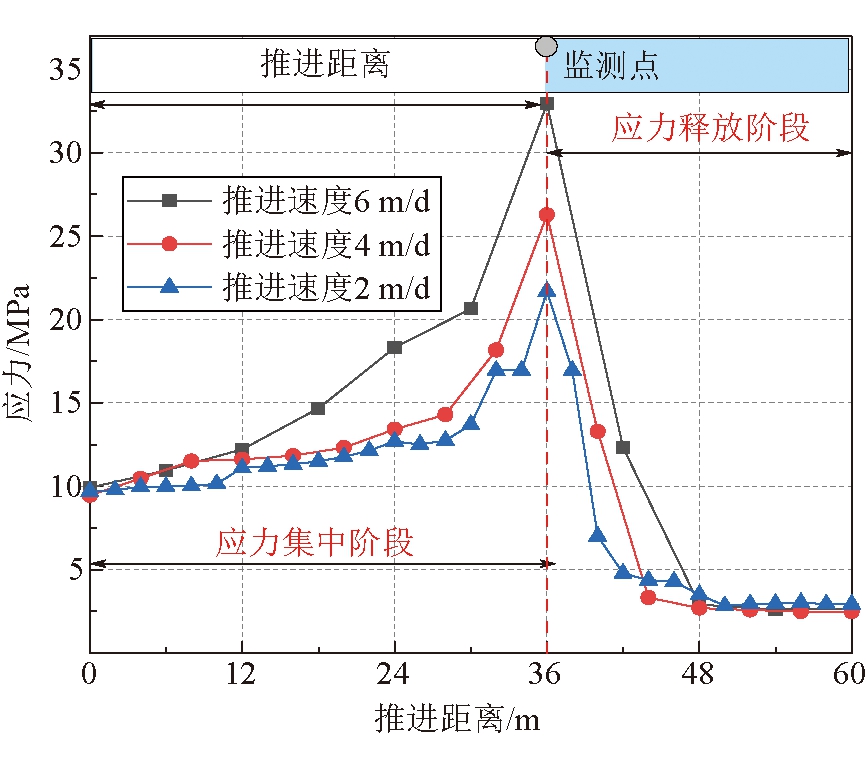
图9 开采过程监测点应力变化曲线
开采过程监测点位移变化曲线如图10所示。由图10可以看出,在煤层开采过程中位移变化规律划分为稳定变化阶段以及骤升阶段。在工作面未达到监测点之前(推进距离小于36 m),此时该测点受开采扰动的影响较小,位移增量小于10 cm,当开采距离大于36 m后,监测点下部采空,受上部煤层顶板、水压力以及地层荷载的共同影响,位移沉降急剧上升,直至开采结束。在煤层开采时,工作面推进速度越快,煤层测点位移沉降量就越大。当煤层开采完成后(推进距离60 m),测点在推进速度2、4、6 m/d时的位移沉降量分别为24.7、31.6、88.9 cm。可以看出工作面推进速度为6 m/d时位移远大于其他工况,因此煤层开采应注意工作面推进速度以确保施工安全。

图10 开采过程监测点位移变化曲线
开采过程监测点水压力变化曲线如图11所示。由图11可以看出,3种工况下水压力变化规律均呈现出稳定变化阶段及骤升阶段2种变化阶段,且分界点均位于工作面推进至测点所在截面(推进距离36 m),此时,由于煤层采空,导致上部积水异常区涌水沿着此煤层顶板裂隙涌入采空区,导致水压骤升。最终水压力随工作面推进速度的增加而略有增大,当推进距离达到60 m时,工作面推进速度为2、4、6 m/d工况时水压力分别为633、666、713 kPa。
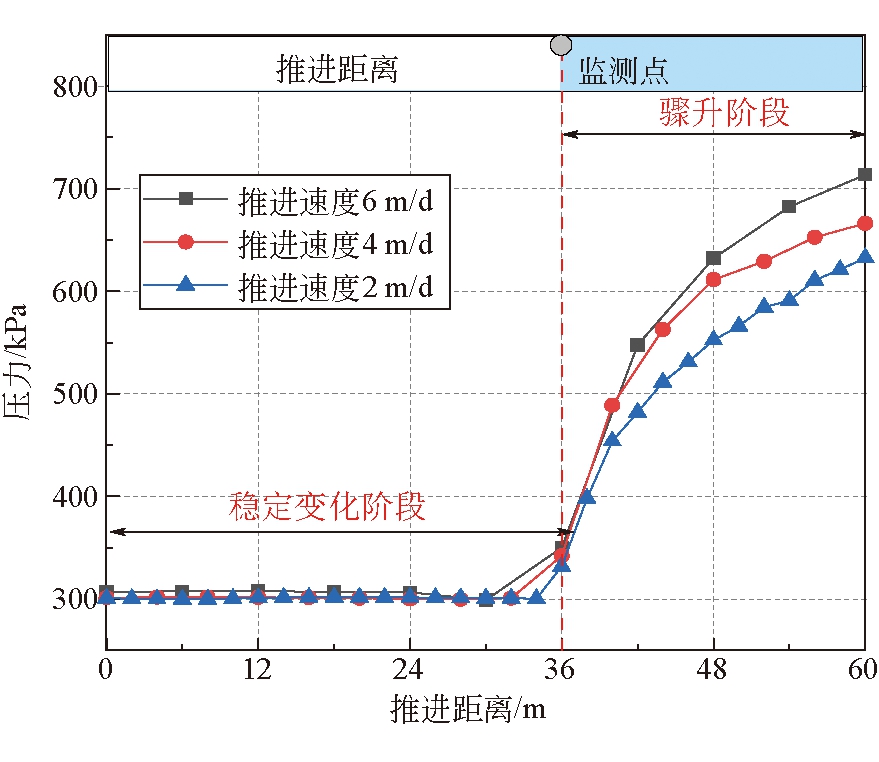
图11 开采过程监测点水压力变化曲线
开采过程监测点塑性应变变化曲线如图12所示。由图12可以看出,在工作面未推进至监测面时(推进距离36 m),开采扰动并未波及监测点,因此基本未产生塑性应变。当工作面推进至此处时,塑性应变急剧上升,发生塑性应变突变,之后随着煤层开采又平稳增加。此外,工作面推进速度越快,应变突变增量就越大。最终开采完毕后,该测点在工作面推进速度为2、4、6 m/d时塑性应变分别为0.002 11、0.012 14、0.017 34,可见不同的工作面推进速度对煤岩层塑性应变的影响程度显著。

图12 开采过程监测点塑性应变变化曲线
4 结论
通过有限元软件ABAQUS模拟在上方有采空区积水的条件下,下方煤层开采时工作面分别以2、4、6 m/d的推进速度对煤岩层结构安全稳定性的影响。分析得出在采空区积水及煤层不同开采速度共同作用影响下,煤岩层的应力、位移、水压力以及塑性应变规律。
(1)煤层开采后煤岩体的原始应力场遭受破坏,工作面附近产生应力集中,随着工作面的推进,工作面处应力集中现象越发显著,且推进速度越快,应力峰值也越大。
(2)工作面推进过程中煤岩层的位移沉降规律经历了积水影响异常区、工作面沉降影响区以及上下煤层沉降贯通区3个阶段过程,工作面推进速度越快,煤层开采区域位移沉降量就越大。
(3)水压力随工作面推进速度的增加而略有增大,但不同推进速度对煤层开采的水力渗流影响不大。
(4)对于煤岩层损伤方面,随工作面与积水区距离逐渐缩短,最终诱发上部积水异常范围产生塑性区并与下部煤层贯通。工作面推进速度越快,开采扰动产生的煤岩层损伤范围就越大,塑性应变峰值同样增大。
[1] 景国勋,秦瑞琪.2011-2020年我国煤矿水害事故相关因素特征分析[J].安全与环境学报,2022,22(4):2297-2304.
[2] 张楠.慈林山矿上覆采空区积水煤层开采突水危险性评价[J].煤炭与化工,2022,45(7):50-53,56.
[3] CHEN Zihan,ZOU Quanle,GAO Shikang,et al. Long-term evolution of overlying rock fractures in mined-out areas and its effect on gas flow conductivity[J]. Fuel,2023,353:1-10.
[4] CUI Chuanbo,JIAO Zhipeng,ZHOU Yuying,et al.Experimental study of three-dimensional time domain of water evaporation from goaf[J]. Applied Sciences,2023,13(13):1-10.
[5] LIU Wei,ZHANG Fengjie,GAO Tiegang,et al. Efficient prevention of coal spontaneous combustion using cooling nitrogen injection in a longwall gob:An application case[J]. Energy,2023,281:1-10.
[6] 冯国瑞,张玉江,戚庭野,等. 中国遗煤开采现状及研究进展[J]. 煤炭学报,2020,45(1):151-159.
[7] 王珩珩.关于未来煤炭开采技术发展方向的探讨[J].当代化工研究,2022(1):7-9.
[8] 刘福胜. 基于流固耦合及复变函数分析的隧道渗流问题研究[D].广州:华南理工大学,2012.
[9] 郑颖人. 岩土塑性力学原理:广义塑性力学[M]. 北京:中国建筑工业出版社,2002.
Research on the influence of working face advancing speed on the stability of coal and rock strata under the condition of water accumulation in goaf

移动扫码阅读
JIN Zhupeng,XU Yaming. Research on the influence of working face advancing speed on the stability of coal and rock strata under the condition of water accumulation in goaf [J]. China Coal,2023,49(8):26-33.DOI:10.19880/j.cnki.ccm.2023.08.005
- 相关推荐
