基于GM(0,n)灰色预测模型的构造预测及定量评价
时间:2022-02-10 来源:中国煤炭杂志官网 分享:★ 智慧矿山 ★
基于GM(0,n)灰色预测模型的构造预测及定量评价
我国煤系地层复杂的构造条件是各类地质条件形成的主控因素,严重制约着我国煤炭的安全高效开采。近年来,不断提高的煤矿生产机械化程度要求对井田的构造规律做出更加深入的研究。许多矿井地质构造条件复杂,且对矿井未采区域地质构造规律的认识模糊不清,导致采掘工作常常处于被动局面,直接制约着煤炭产量、威胁着生产安全。这就需要在采掘工程未开始前,能够对未采区域的构造复杂程度做出一定的预判。受限于传统的构造规律研究方法,急需从构造的预测及定量评价这一难题中寻求突破口。能否在采掘工程开始前,通过量化研究得出未采区采掘范围内构造的发育规律,成为了煤矿实现生产安全以及提高经济效益的关键。
从矿井构造预测概念的提出到目前判别分析法、构造指数法、等性块段法、模糊综合判断法、灰色系统理论及人工神经网络等多种定量化评价预测方法的应用,国内外学者在构造定量化研究方面做了大量工作。为了得到与实际矿井揭露基本一致的预测评价结果,基于对井田构造发育规律的充分分析,选取最优评价指标,结合灰色模糊综合评价和灰色系统建模的方法对井田未采区域地质构造的复杂程度进行了量化研究和综合评价。
1 井田概况
芦岭井田位于宿东向斜西南翼的东南段,含煤地层为石炭、二叠系,主采8#、9#、10#煤层。斜切断层在井田内较为发育,走向以NNE、NE向为主,NW、NNW向次之,总体呈现为局部断层密集,切割关系复杂,力学性质扭性为主;井田内的褶皱构造有:宿东、王格庄向斜及小史家背斜等,断裂构造多分布于应力集中的褶皱轴部,且小断层、小褶皱也分布较多。普遍发育的层滑构造对主采煤层造成大面积破坏,对生产造成了很大影响。
目前,该井田一水平已回采完毕,二水平正在开采,三水平处于准备阶段,针对井田未采掘区域开展构造预测及地质构造复杂程度定量评价,不仅给未采区在采掘规划的形成和开采方式的选取上提供了理论依据,也对矿井的可持续发展、安全高效开采意义重大。
2 定量评价指标的确定
作为定量评价地质构造复杂程度的基础,评价指标的确定直接关系到评价结果的准确性。鉴于不同区域不同井田多样化的构造条件以及开采方式、生产机械化程度的差异,统一的指标体系套用是不可取的,必须与矿井实际情况紧密结合。在此基础上,才能合理地确定矿井定量评价的指标。
井田内构造以断裂构造为主,由于已采区的范围较广,地质勘探及采掘揭露数据较多,可较易获取各类构造复杂程度定量化研究所需的经济、技术指标;而对于未采区,勘探工作尚未全面开展,部分评价指标不容易获取。因此,结合矿井地质构造特征和生产的需要,本文选取全矿井评价指标和已采区评价指标两类指标。
2.1 全矿井评价指标
(1)褶皱复杂型指数(W)。它反映褶皱的紧密程度和煤层倾角大小的变化关系。
(1)
式中:![]() 统计单元内底板等高线曲率均值,rad;
统计单元内底板等高线曲率均值,rad;
n——统计单元内等高线条数,条。
(2)断裂分维值(K)。它是反映断裂构造复杂程度的一种准确有效的指标。本次采用计盒维数法,在煤层底板等高线图上分别划分了250 m×250 m、125 m×125 m及62.5 m×62.5 m的网格,通过计算得到断裂分维值。
(3)煤层底板倾角变异系数(R)。它反映统计单元内煤层倾角的变化程度。
(2)
式中:![]() 煤层平均倾角,(°);
煤层平均倾角,(°);
ai——第i个统计单元的煤层倾角,(°);
n——统计单元数。
2.2 已采区评价指标
(1)断层密度(M)。它反映一定范围内断层的发育程度。
(3)
式中:k——断层数,条;
S——统计单元面积,104m2。
(2)断层强度(F)。它反映断裂构造的发育程度。
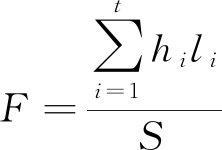
(4)
式中:li——第i断层的水平延伸长度,m;
hi——第i断层的水平延伸长度和落差,m。
(3)断层走向影响指数(Q)。它反映不同走向断层对生产的影响。
(5)
式中:θi——断层与煤层的走向夹角,(°);
Li——断层水平延伸长度,m;
n——断层条数,条。
(4)褶皱平面变形系数(P)。它反映褶皱构造复杂程度。
(6)
式中:h0——相邻两条等高线的标高差,m;
L0——计算单元中心两条等高线间的水平距离,m;
L1——靠近计算单元中心的等高线在单元内的实际长度,m;
L2——靠近计算单元中心的等高线在单元内的割线长度,m。
3 定量评价标准
结合井田构造特点,依据《矿井水文地质规程》中地质构造4类划分法,得到井田已采区各评价指标的复杂程度分类标准(表1)。依据表1构造复杂程度分类标准,构建了井田已采区地质构造复杂程度定量评价模型,划分了简单、中等、复杂和极复杂4类构造等级,评价结果基本符合矿井实际揭露情况,证实了评价结果的合理性,可以作为未采区构造复杂程度定量评价的标准。
表1 井田已采区各评价指标的复杂程度分类标准
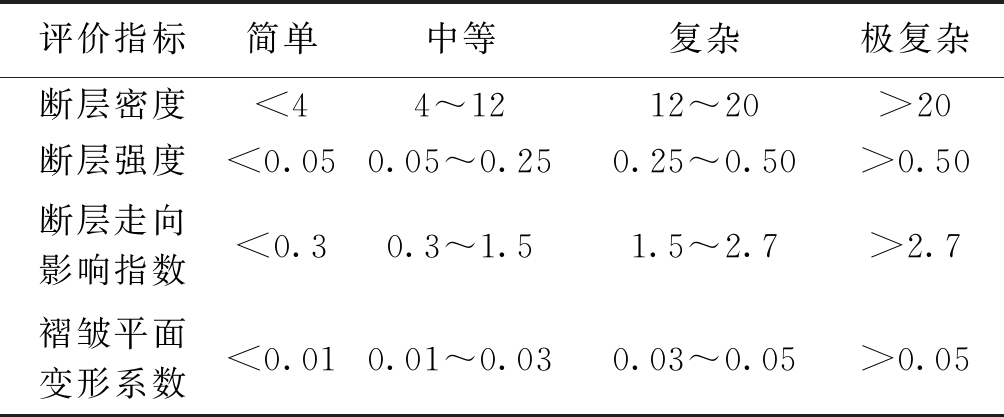
评价指标简单中等复杂极复杂断层密度<44~1212~20>20断层强度<0.050.05~0.250.25~0.50>0.50断层走向影响指数<0.30.3~1.51.5~2.7>2.7褶皱平面变形系数<0.010.01~0.030.03~0.05>0.05
4 未采区构造预测
4.1 定量预测模型的建立
灰色预测模型种类较多,有多种可用于本次模型的建立。基于对井田内定量化评价指标可选择度以及可选择指标大数据真实度上的综合考虑,本次选择GM(0,n)模型,即用零阶微分方程建立n个变量的静态数学模型来建立定量预测模型。
(1)数学模型。GM(0,n)数学模型:
(7)
式中:a、bi——待定系数,其中,i=1,2,……,n-1;
xi(1)——第i个变量的原始数据累加处理后的取值。
记原始数据序列为:
一次累加处理后的数据序列为:
其中,![]()
记:
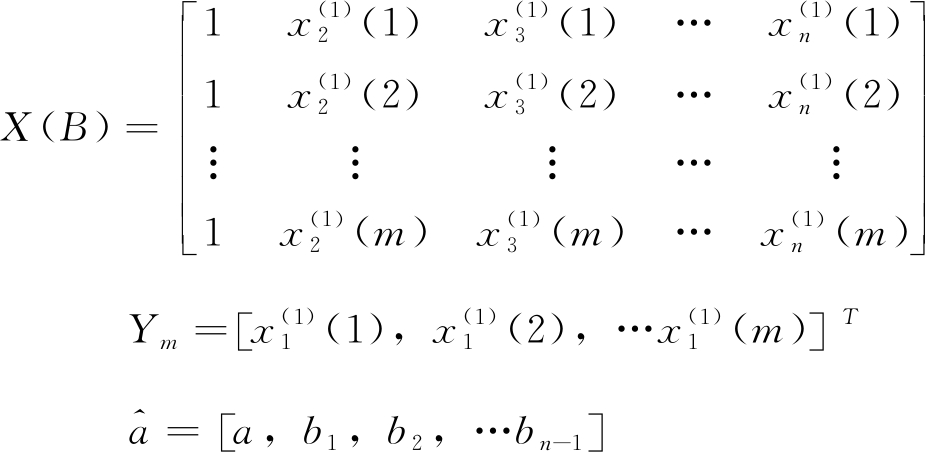
由最小二乘法可求得:
(8)
将式(2)计算结果代入式(1),得到GM(0,n)模型。
(2)预测模型。首先,对已采区内的7个评价指标,即断层密度、断层强度、断层走向影响指数、褶皱平面变形系数、褶皱复杂性指数、断裂分维值及煤层底板倾角变异系数进行了统计分析,继而运用GM(0,n)灰色预测模型建立了各评价指标的GM(0,4)构造预测模型:
①断层密度(M):M=-0.8209×W+12.6460×K+16.4047×R-11.2466
(9)
②断层强度(F):F=-0.001×W+0.0654×K-0.0169×R+0.0565
(10)
③断层走向影响指数(Q):Q=-0.0712×W+1.6589×K+3.1076×R-0.0028
(11)
④褶皱平面变形系数(D):D=0.0002×W+0.0147×K-0.0250×R+0.0107
(12)
4.2 预测模型检验
先依次将xi(1)(t)(i=1,2,……,n;t=1,2,……,m)带入GM(0,n)模型,得到因变量的预测值![]() 然后求出其实测值的残差δ(t)与相对误差δt。如果max{δt,t=1,2,……,m}≤5%,则认为该模型的预测精度符合要求。下面依次检验已采区内4个评价指标的灰色预测模型残差和相对误差,检验结果见表2。
然后求出其实测值的残差δ(t)与相对误差δt。如果max{δt,t=1,2,……,m}≤5%,则认为该模型的预测精度符合要求。下面依次检验已采区内4个评价指标的灰色预测模型残差和相对误差,检验结果见表2。
据表2可知,本次建立的GM(0,4)灰色预测模型相对误差都在5%之内,预测精度较好,可以用于未采区的地质构造预测。
4.3 未采区构造定量评价
依据上面建立的GM(0,4)构造预测模型,以未采区10#煤层底板等高线为底图,在图上选取平行和垂直煤层总体走向的网格线来绘制正方形网格单元,累计划分500 m×500 m网格19个,并对每个网格单元内褶皱复杂性指数、断裂分维值及煤层底板倾角变异系数的值进行统计,然后通过GM(0,4)构造预测模型得到断层密度、断层强度、断层走向影响指数和褶皱平面变形系数的参数值,如表3所示。
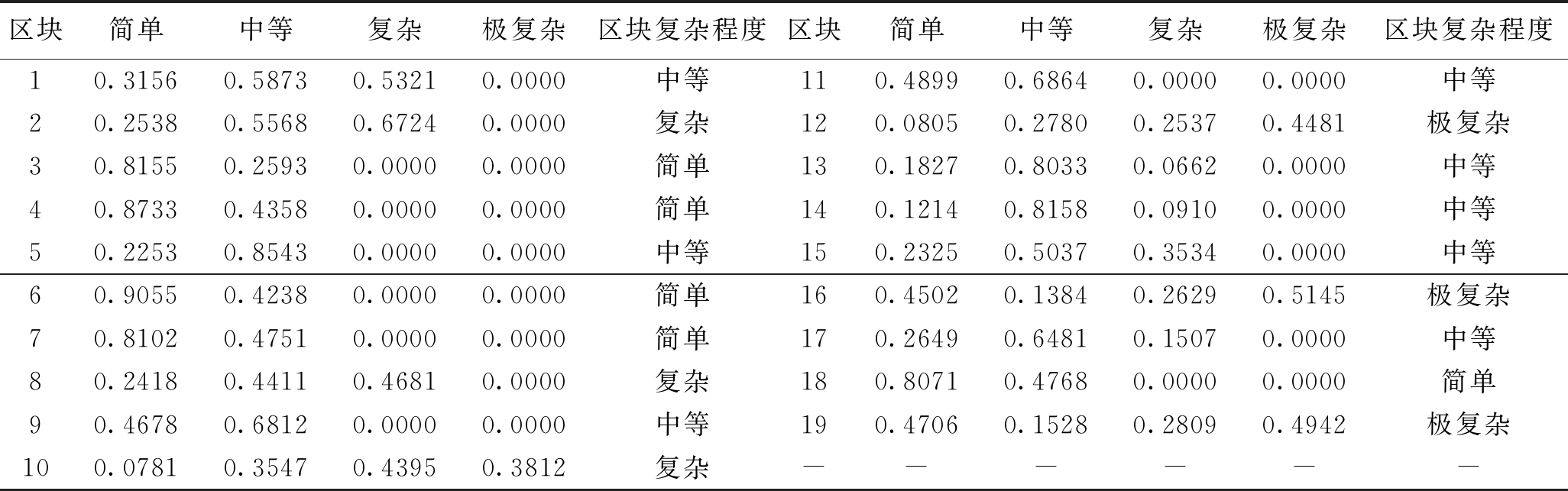
继而借助灰色模糊综合评价方法,采用因素权重和评价指标程度权重相结合的双权重,并根据井田已采区构造复杂程度定量评价标准,求出未采区地质构造复杂程度评价系数的计算结果,见表4。根据最大隶属度原则,完成了井田未采区地质构造复杂程度的定量评价,如图1所示,划分了构造简单、构造中等、构造复杂和构造极复杂4类构造等级,并明确了各构造等级的分布状况。
表2 井田已采区评价指标误差检验表
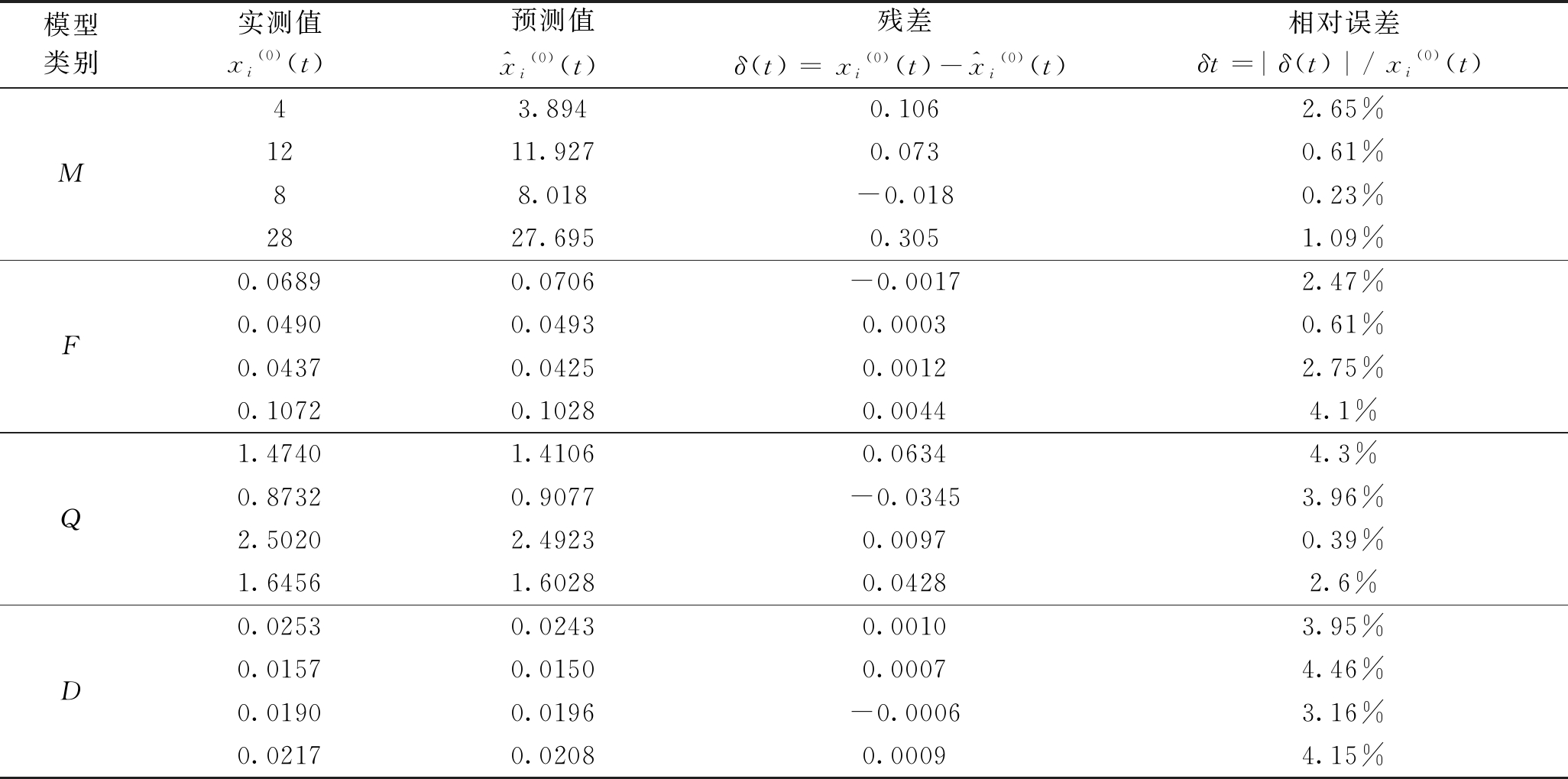
模型类别实测值xi(0)(t)预测值^xi(0)(t)残差δ(t)= xi(0)(t)-^xi(0)(t)相对误差δt=|δ(t)|/ xi(0)(t)M43.8940.1062.65%1211.9270.0730.61%88.018-0.0180.23%2827.6950.3051.09%F0.06890.0706-0.00172.47%0.04900.04930.00030.61%0.04370.04250.00122.75%0.10720.10280.00444.1%Q1.47401.41060.06344.3%0.87320.9077-0.03453.96%2.50202.49230.00970.39%1.64561.60280.04282.6%D0.02530.02430.00103.95%0.01570.01500.00074.46%0.01900.0196-0.00063.16%0.02170.02080.00094.15%
表3 未采区各网格单元评价指标预测值

区块断层密度断层强度断层走向影响指数褶皱平面变形系数区块断层密度断层强度断层走向影响指数褶皱平面变形系数140.07291.93140.02121180.02040.11600.0128240.17422.12150.012312240.07622.05860.0302300.00000.00000.013713120.06221.08240.0255440.00410.01160.01441480.04151.52790.0219580.01831.18530.014915120.05700.82490.0320640.00450.18330.01351640.01150.13880.0547740.00330.13540.01631780.03940.02350.02868160.06931.09770.01481840.00320.21270.0163980.03040.22720.01531940.01060.25730.052910200.21942.10490.0114-----
表4 未采区地质构造复杂程度评价系数计算结果
区块简单中等复杂极复杂区块复杂程度区块简单中等复杂极复杂区块复杂程度10.31560.58730.53210.0000中等110.48990.68640.00000.0000中等20.25380.55680.67240.0000复杂120.08050.27800.25370.4481极复杂30.81550.25930.00000.0000简单130.18270.80330.06620.0000中等40.87330.43580.00000.0000简单140.12140.81580.09100.0000中等50.22530.85430.00000.0000中等150.23250.50370.35340.0000中等60.90550.42380.00000.0000简单160.45020.13840.26290.5145极复杂70.81020.47510.00000.0000简单170.26490.64810.15070.0000中等80.24180.44110.46810.0000复杂180.80710.47680.00000.0000简单90.46780.68120.00000.0000中等190.47060.15280.28090.4942极复杂100.07810.35470.43950.3812复杂------
据图1可知,井田大部分未采区域内构造等级中等,构造简单区域主要分布在西部和东部边缘部分,构造复杂和构造极复杂区域分布在未采区的南部和北部,总体上,井田未采区的构造复杂程度属于构造复杂型。

图1 未采区构造复杂程度定量评价结果图
5 结论
本文通过灰色模糊综合评价及灰色建模预测,建立起井田未采区地质构造的定量预测模型,对未采区各评价指标的参数值进行了预测,并依据建立的井田已采区地质构造复杂程度定量评价标准,对未采区地质构造复杂程度做出了定量评价,得到如下结论。
(1)基于对已采区内筛选的7个评价指标参数值的统计分析,借助灰色建模预测方法建立了未采区GM(0,4)灰色构造预测模型,并验证了预测模型预测精度的可靠性,证明了本预测模型可以用于未采区的地质构造预测。
(2)通过建立的未采区地质构造预测模型求得了未采区各评价指标的预测值,并利用建立的已采区地质构造复杂程度定量评价标准完成了未采区构造预测及定量评价,得出在该井田未采区范围内构造简单有5个单元,构造中等有8个单元,构造复杂和构造极复杂各有3个单元。未采区构造中等及中等以上区块占到全区的74%左右,未采区的构造复杂程度总体上属于构造复杂型。
(3)由于该井田未采区实际揭露资料较少,还需进一步探讨和研究构造预测精度等难题,使得到的构造预测结果最大限度地接近地质实际。
[1] 贾建称,陈建,柴宏有等.矿井构造现状与发展趋势[J].煤炭科学技术,2008(10)
[2] 王桂梁,龙荣生,徐凤银等.矿井构造预测[M].北京:煤炭工业出版社,1993
[3] 李增学.马兴祥.实用矿井地质研究——方法与进展[M].北京:中国矿业大学出版社,1993
[4] 徐凤银, 王桂梁,朱兴姗等.矿井地质构造定量预测中的难点及其研究[J].煤田地质与勘探,1992(1)
[5] 周云霞,曹代勇.矿井地质构造定量评价模型探讨[J].煤田地质与勘探,2001(2)
[6] 施龙青,邱梅,韩进等.矿井地质构造定量化预测[M].北京:煤炭工业出版社,2014
[7] 徐凤银,龙荣生,夏玉成等.矿井地质构造定量评价及其预测[J].煤炭学报,1991(4)
[8] 詹才高,范念寒,陆汝纶等.应用等性块段指数法定量划分华北煤矿勘探类型[J].煤田地质与勘探,1995(5)
[9] 徐志斌,王继尧,张大顺等.煤矿断层网络复杂程度的分维描述[J].煤炭学报,1995(5)
[10] 刘德民,曹代勇,李永军等.矿井构造复杂程度模糊综合评判ComGIS的实现[J].煤炭科学技术,2008(2)
[11] 朱宝龙,夏玉成.人工神经网络在矿井构造定量评价中的应用[J].煤田地质与勘探,2001(6)
[12] 王丹丹,施龙青,腾超等.基于GM(0,n)模型的井田未采区构造预测[J].煤炭技术,2016(2)
[13] 张海涛,高珊.阳泉矿区基于分形理论的构造复杂程度定量评价[J].沈阳大学学报(自然科学版),2018(3)
[14] 方家虎,李志,张洋等.芦岭煤矿8煤层地质构造复杂程度综合评价[J].煤田地质与勘探,2016(1)
[15] 李鹏.邢东煤矿地质构造分析与评价[D].西安科技大学,2011
[16] 武昱东,琚宜文,侯泉林等.断层分层信息维及其在深部煤炭开采地质条件预测中的应用[J].煤炭学报,2010(8)
[17] 刘思峰,郭天榜,党耀国.灰色系统理论及其应用(第六版)[M].北京:科学出版社,2010
[18] 高荣斌,闫明,张东营.构造发育复杂性评价方法研究及应用[J].中国煤炭,2013(6)
[19] 任小强.矿区未采区构造复杂程度的综合评价与灰色预测[J].煤矿现代化,2018(6)
Structure prediction and quantitative evaluation based on GM(0,n) grey prediction model
- 相关推荐
